Synopsis

An artificial 3D capillary-network phantom (made out of melt-spun sugar fibers) was characterized with diffusion-time-dependent diffusion-weighted MRI. Restricted diffusion was analyzed based on a two-compartment (cylinders and spheres) model; diffusion coefficients were simulated with a simple random-walk model of spins in 2D and 3D spherical geometries. The best model fit agreed very well with the measured diffusion-time-dependent diffusion coefficients and resulted in a mean diameter of 142±2 µm of the spheres and a mean diameter of 9.7±0.7 µm of the capillary tubes (cylinders) with a capillary fraction of f_cyl=35±1%.

Introduction

Diffusion-weighted magnetic resonance imaging (DW-MRI) allows for the quantification of the random motion of self-diffusing water molecules in biological tissue by calculating the apparent diffusion coefficient (ADC). If diffusion is geometrically restricted, the mean diffusional displacement is smaller than in the case of free diffusion and the calculated ADC decreases with increasing diffusion time in a characteristic way depending on the confining geometry.

The aim of this project was to measure the water self-diffusion within an artificial 3-dimensional capillary network phantom as a function of the diffusion time and to demonstrate that diffusion-time-dependent DW-MRI measurements can be utilized to determine quantitatively the geometric properties of a capillary network phantom.

Methods

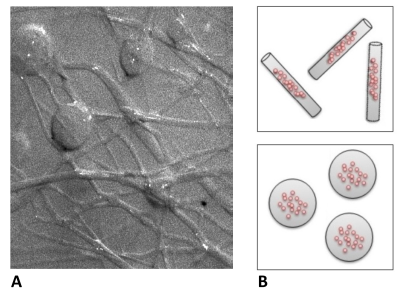
The capillary network phantom was made out of melt-spun sugar fibers produced with a cotton-candy machine and embedded into synthetic resin as previously described^1,2; it consisted of thin cylindrical capillaries (with diameters of about 10 µm) and connected larger spherical dilations (with diameters of about 100 µm); cf. Fig. 1A. Due to the very small diameters of the artificial capillaries in the micrometer range, which is comparable to in-vivo structures, self-diffusion of water molecules is substantially restricted. The diffusion of an aqueous sodium-chloride solution (with a NaCl concentration of 213 g/L to match the magnetic susceptibility to the used resin) outside and inside the capillary phantom was measured at a clinical 3-Tesla MRI system (Magnetom Skyra, Siemens Healthcare, Erlangen, Germany) using a stimulated-echo DW-MRI sequence with 11 b-values between 100 and 300 s/mm². Diffusion times τ were varied from 17 to 1012 ms in 22 steps.

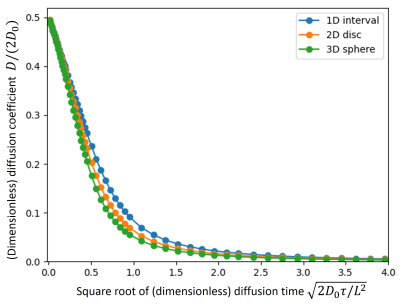
Restricted diffusion was simulated in 2D and 3D spherical unit structures (radius R=0.5) with a simple random-walk approach (500,000 samples; 150,000 random-walk steps; 61 diffusion times; cf. Fig. 2). All simulations were performed in dimensionless quantities and were later re-scaled to physical units³. Diffusion in isotropically oriented (infinite) cylinders was modeled by combining 1D unrestricted diffusion (with diffusion coefficient D₀) and 2D restricted spherical diffusion (i.e., diffusion in a disc) as

$$D_{\mathrm{cyl}}(\tau)=\frac{2D_{\mathrm{disc}}(\tau)+D_0}{3}.$$

The phantom was then modeled as a combination of cylindrical (D_cyl(τ)) and spherical (D_sphere(τ)) structures (cf. Fig. 1B) with a variable volume fraction f_cyl of the cylindrical compartment.

All simulations and data processing were performed with Python and the NumPy/SciPy framework.

Results

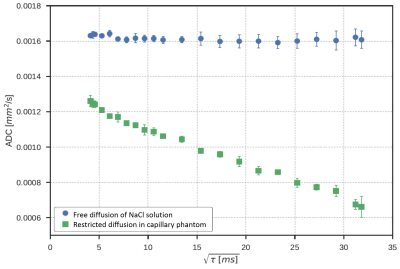
The free diffusion coefficient of the aqueous sodium-chloride solution was D₀=1.61±0.01 µm²/ms (Fig. 3, blue circles). The measured diffusion coefficients in the phantom showed substantially decreasing diffusion coefficients from 1.26 to 0.66 µm²/ms with increasing diffusion times (Fig. 3, green squares).

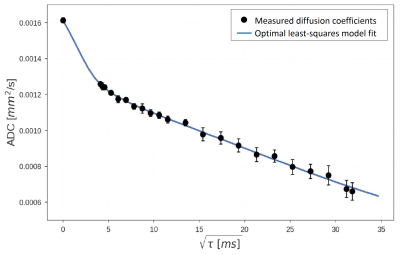
By fitting the random-walk-based 2-compartment model to the measured data (including the value D₀ for diffusion time 0), a very good agreement of the model function and the measured data points was found (Fig. 4). The best fit was obtained for a mean diameter of 142±2 µm of the 3D spheres and a mean diameter of 9.7±0.7 µm of the capillary tubes (cylinders) with a capillary fraction of f_cyl=35±1%.

Discussion

The free diffusion coefficient of 1.61±0.01 µm²/ms of the sodium-chloride solution agrees well with results found in literature^4,5; the ADC showed a decrease to 78 % of the ADC of purified water due to the structure-making properties of NaCl.

The diffusion-time dependence of the ADC with two different regimes (Fig. 4) reflects first highly restricted diffusion in smaller cylindrical geometries (up to τ=25 ms), and less restricted diffusion in bigger spherical dilations at longer diffusion times. The MRI-measured diameter of the cylinders (of 9.7±0.7 µm) agrees very well with measurements from optical microscopy of 11±4 µm. The MRI-measured diameters of the spheres (142±2 µm) deviate from the light-microscopy results of 62±21 µm by a factor of about 2.3. This may be explained by the relatively small part of the phantom (close to its surface) that is accessible by optical microscopy; larger spheres might be found in more central areas. In addition, the diameters of the spheres will be distributed over a certain range, and larger diameters are weighted more strongly in MRI due to the larger volume and proton content (the weighting depends cubic on the diameter and thus larger spheres will be overrepresented in the MRI results). More detailed models based not only on an average diameter but a statistical distribution of diameters might be a method to resolve these remaining issues in future studies.

Conclusion

Acknowledgements

References

1. Gaass T, Schneider MJ, Dietrich O et al. Technical Note: Quantitative dynamic contrast-enhanced MRI of a 3-dimensional artificial capillary network. Med Phys 2017;44(4):1462-1469.

2. Bellan LM, Singh SP, Henderson PW et al. €˜Fabrication of an artificial 3-dimensional vascular network using sacrificial sugar structures€™. Soft Matter 2009;5(7):1354-€“1357.

3. Dietrich O, Hubert A, Heiland S. €˜Imaging cell size and permeability in biological tissue using the diffusion-time dependence of the apparent diffusion coefficient€™. Phys Med Biol 2014;59(12):3081-3096.

4. Müller KJ, Hertz HG. €˜A parameter as an indicator for water-water association in solutions of strong electrolytes€™. J Phys Chem 1996;100(4):1256-€“1265.

5. Harris KR, Mills R, Back PJ et al. An improved NMR spin-echo apparatus for the measurement of self-diffusion coefficients: the diffusion of water in aqueous electrolyte solutions€™. J Magn Reson 1978;29(3):473-€“482.