0818
Deep Learning for Magnetic Resonance Fingerprinting: Data Augmentation with Phase Encoding and SVD Preprocessing for Accurate Parameter Reconstruction of FISP Data.1Department of Physics and Astronomy, Univeristy of Bologna, Bologna, Italy, 2Department of Radiology, Stanford, Stanford, CA, United States, 3Department of Electrical Engineering, Stanford, Stanford, CA, United States, 4Department of Physics and Astronomy, University of Bologna, Bologna, Italy, 5Department of Radiology, Stanford University, Stanford, CA, United States, 6Department of Bioengineering, Stanford University, Stanford, CA, United States, 7Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 8University of Bologna, Bologna, Italy, 9Department of Biomedical and NeuroMotor Sciences, University of Bologna and Functional MRUnit, Policlinico S. Orsola - Malpighi, Bologna, Italy
Synopsis
Dictionary size limits the number of parameters one can aim to estimate with Magnetic Resonance Fingerprinting (MRF) Deep Neural networks (NN) have been recently proposed for MRF applications, both with numerical simulationsand with phantoms and in-vivo acquisitions. With real-valued NNs only the magnitude of the MRF signal has been considered as input. This choice releases from the need of considering the phase of the signal during training but can affect noise robustness and signal differentiation due to loss of information. In this work we propose a strategy to train a real valued NN that takes the real and imaginary parts of an MRF-FISP signal as input. We also propose to use SVD as preprocessing step for noise reduction. The presented results may help the developing of deep learning approaches for MRF, pushing fingerprinting pulse sequences design to add more meaningful MR parameters, such as diffusion, with no more limitations due to the dictionary size.
Introduction
Dictionary size limits the number of parameters one can aim to estimate with Magnetic Resonance Fingerprinting1 (MRF). Big dictionaries are hard to handle because they are costly both in memory usage efficiency and in computational time for the matching procedure. Deep Neural networks (NN) have been recently proposed for MRF applications, both with numerical simulations2,3 and with phantoms and in-vivo acquisitions4,5. With real-valued NNs only the magnitude of the MRF signal has been considered as input3,4,5. This choice releases from the need of considering the phase of the signal during training but can affect noise robustness and signal differentiation due to loss of information. In this work we propose a strategy to train a real valued NN that takes the real and imaginary parts of an MRF-FISP signal as input. We also propose to use SVD6 as preprocessing step for noise reduction. The presented results may help the developing of deep learning approaches for MRF, pushing fingerprinting pulse sequences design to add more meaningful MR parameters, such as diffusion, with no more limitations due to the dictionary size.Methods
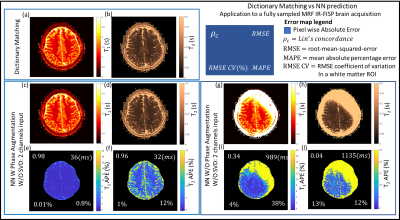
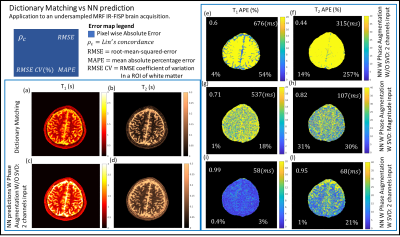
The IR-FISP MRF pulse sequence as described in article7 was used in this work. The NN application was developed using Keras with TensorFlow backend. Fig. 1 depicts the NN model along with the procedure used to train it. Two training data sets were generated (one per acquisition scheme) by simulating the MRF signals from 120000 (T1,T2) pairs sampled from an uniform distribution (T1 : [10 ÷ 4000]ms and T2 : [5 ÷ 3000]). The SVD matrixes used to perform preprocessing were computed from the training data sets. Two volunteers were scanned at 3T under IRB approval using an 8-channel head coil (FOV 22 x 22 cm, resolution 1.2 mm, slice thickness 5 mm). A fully sampled scan (400 TRs, 36 spiral interleaves) and an undersampled scan (1000 TRs, 1 spiral with 89 interleaves) were acquired for this study. T1 and T2 maps where reconstructed using a conventional dictionary approach and NNs trained with different training procedures. Mean-absolute-percentage-error (MAPE), root-mean-squared-error (RMSE) and Lin’s concordance coefficient (rc) between MR parameters estimated using the dictionary and NN approaches were used as quality metrics. The scalp region was not considered in the computations. Coefficient of variation (CV) for MR parameters was also evaluated in a white matter ROI.Results
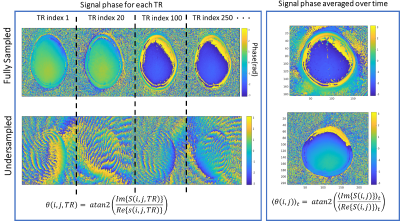
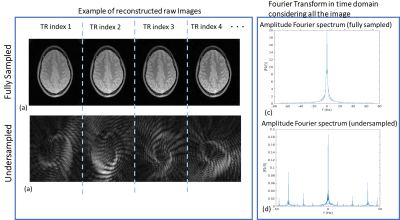
Fig. 2 shows the phase evaluation for the fully and undersampled scans. In both cases the phase is not stationary and not homogenous across the slice. Fig. 3 shows, both for the fully and undersampled scans, examples of raw reconstructed images for four TRs (left box). The Fourier spectrum of the signal evolution considering all the image is showed in the right box, which reveals that the undersampling creates noise peaked on specific frequencies instead of being white. The performance of the NN trained with and without the phase augmentation step (both without SVD preprocessing) against the dictionary approach are reported in Fig.4 for the fully sampled acquisition. When the phase is considered during training the quality metrics exceed those obtained without considering it both for T1 ( rc: 0.98>0.34) and T2 (rc: 0.96>0.04). The performance of the NN trained with and without SVD preprocessing against the dictionary approach are reported in Fig.5 for the undersampled acquisition. Using both the real and imaginary part of the signal with SVD preprocessing gave the best results (T1: rc =0.99 and T2: rc =0.95)Discussion
Fig.1 shows phase is not homogenous across the image and considering phases during NN training is crucial to use real and imaginary parts as input (see Fig.4). Whit Gaussian noise is a poor model when acquisition is undersampled making the NN to producing inaccurate parameter estimations. SVD can be used as preprocessing step to reduce noise and make the NN able to largely improve in performance. Fig. 5 also shows as using the magnitude of the signal as input brings to much less accuracy in parameter estimations in respect with real and imaginary parts used as input.Conclusion
A strategy to efficiently train real-valued NN to handle real and imaginary parts of the MRF IR-FISP signal has been proposed by considering different phase during training. Noise due to undersampling can then be reduce using SVD and produce MR parameters maps very comparable with those obtained with the standard method. The results may help the developing of deep learning approaches for MRF, pushing fingerprinting pulse sequences design to add more meaningful MR parameters, such as diffusion, with no more limitations due to the dictionary size.Acknowledgements
No acknowledgement found.References
[1] D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, M. A. Griswold, Magnetic resonance fingerprinting, Nature 495 (2013).
[2] P. Virtue, S. X. Yu, M. Lustig, Better than Real: Complex-valued Neural Nets for MRI Fingerprinting, ArXiv e-printsarXiv:1707.00070.
[3] E. Hoppe, G. K¨orzd¨orfer, T. W¨urfl, J. Wetzl, F. Lugauer, J. Pfeuffer, A. K. Maier, Deep learning for magnetic resonance fingerprinting: A new approach for predicting quantitative parameter values from time series, Studies in health technology and informatics 243 (2017) 202–206.
[4] O. Cohen, B. Zhu, M. S. Rosen, Mr fingerprinting deep reconstruction network (drone), Magn. Reson. Med 80 (3) (2018) 885–894. doi:10.1002/mrm.27198.
[5] F. Balsiger, A. Shridhar Konar, S. Chikop, V. Chandran, O. Scheidegger, S. Geethanath, M. Reyes, Magnetic Resonance Fingerprinting Reconstruction via Spatiotemporal Convolutional Neural Networks, ArXiv e-printsarXiv:1807.06356.
[6] D. F. McGivney, E. Pierre, D. Ma, Y. Jiang, H. Saybasili, V. Gulani, M. A. Griswold, Svd compression for magnetic resonance fingerprinting in the time domain, IEEE Trans. Med. Imaging 33 (12) (Dec. 2014) 2311–2322.
[7] Y. Jiang, D. Ma, N. Seiberlich, V. Gulani, M. A. Griswold, Mr fingerprinting using fast imaging with steady state precession (fisp) with spiral readout, Magn. Reson. Med. 74 (6) (2014) 1621–1631. doi:10.1002/mrm.25559.
Figures