Synopsis

The main characteristic of an MRF sequence is the simultaneous application of (a) transient states excitation and (b) highly undersampled k-space. Despite the promising empirical results obtained with MRF, no work has appeared that formally describes the combined impact of these two aspects on the reconstruction accuracy. We derive a mathematical model that directly relates the time varying RF excitation and the k-space sampling to the spatially dependent reconstruction errors. An in-depth analysis of the model reveals that, analogously to the compressed sensing framework, incoherence plays a fundamental role also in MRF.

Introduction

Theory

In the following $$$x$$$ denotes position; $$$\theta=(T_1,T_2,\rho)$$$ denotes the spatially dependent parameters; $$$M(\theta)=(M_1(\theta),\ldots,M_{N_{\rm{}I}}(\theta))$$$ denotes the time-dependent magnetization response; $$$I(x)=(I_1(x),\ldots,I_{N_{\rm{}I}}(x))$$$ are the undersampled images.

The MRF reconstructed parameters $$$\theta^*(x)$$$ can be mathematically characterized⁶ as the critical points of the least-squares objective function $$$\parallel{}M(\theta)-I(x)\parallel^2$$$. Formally, the requirement is that$$\left.\frac{\partial}{\partial\theta_p}\parallel{}M(\theta)-I(x)\parallel^2\right|_{\theta=\theta^*(x)}=0,\qquad{}p=1,2,3,$$which yields the so-called normal equations.

These equations can be simplified considerably by a linearization. Using the decomposition$$\theta(x)=\theta_0+\theta_1(x),$$where $$$\theta_0$$$ is a fixed reference value and $$$\theta_1(x)$$$ is the spatially dependent contrast term, the magnetization response satisfies$$M(\theta)\approx{}M(\theta_0)+\mathcal{D}M(\theta_0)\theta_1,$$where $$$\mathcal{D}M(\theta_0)$$$ is the Jacobian matrix evaluated at $$$\theta_0$$$. Formulating the normal equations, inserting the linear approximation and rewriting yields$$\text{error}(x)=\epsilon_1(x)+\epsilon_2(x,\theta_1(\cdot))+\text{higher order terms,}$$where $$$\epsilon_1$$$ and $$$\epsilon_2$$$ are error terms, such that $$$\epsilon_1$$$ is independent of the object properties $$$\theta_1$$$ and $$$\epsilon_2$$$ depends linearly on the function $$$\theta_1$$$.

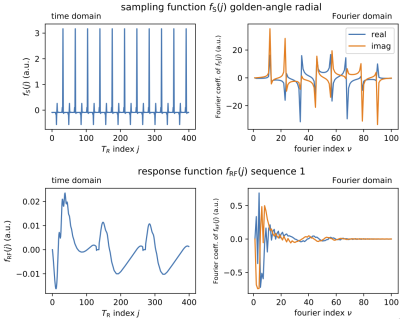
The analysis of $$$\epsilon_1(x)$$$ and $$$\epsilon_2(x)$$$ leads to a novel incoherency concept for MRF. We observe linear relationships between the true Fourier transformed values $$$\widehat{\theta}_1(k)$$$ and $$$\widehat{\epsilon}_2(k)$$$, given for each k by a $$$3\times{}3$$$ matrix $$$\mathcal{E}(k)$$$. The matrix coefficients are inner products of two vectors. The first vector, $$$f_{\rm{}S}(j)$$$, depends on the time-dependent k-space sampling pattern at the j-th snapshot. For each time point j, the average k-space sampling is subtracted. The second vector depends on the transient state excitation response and is given by$$f_{{\rm{}RF}}(j)=\sum_{r=1}^3(\mathcal{D}M^*\,\mathcal{D}M)^{-1}_{p,r}\overline{\mathcal{D}M_{j,r}}\mathcal{D}M_{j,q}.$$Contributions to the error are directly proportional to the innerproducts $$$\sum_{j=1}^{N_{\rm{}I}}\overline{f_{{\rm{}RF}}(j)}f_{\rm{}S}(j)$$$. Therefore to minimize the error, the quantities $$$f_{\rm{}S}$$$ and $$$f_{{\rm{}RF}}$$$ should destructively interfere, or, in other words, be mutually incoherent.

Methods

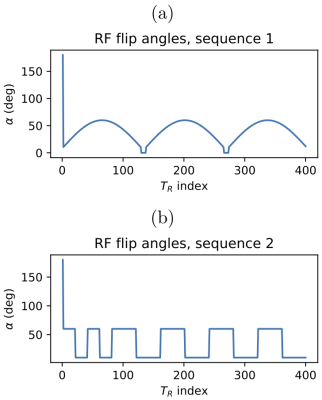
The validation of our error model, and hence of the incoherency criterion, is done using numerical simulations, since the ground truth is required. The examples focus on 2D gradient spoiled sequences with radial and spiral $$$k$$$-space sampling. Figure 1(a) shows the flip-angle train, with 400 intervals. The undersampling factor is 32, while $$$(T_{\rm{}R},T_{\rm{}E})=(15,7.5)$$$ms. The reference value $$$\theta_0$$$ is the average of white and grey matter values. A checkerboard and a brain phantom⁷ ($$$128\times{}128$$$ voxels) are considered, see Figures 2(a,e).

Next we show how, in the new model, different sequence characteristics influence accuracy. Two flip-angle trains (see Figure 1(a,b)) and radial $$$k$$$-space sampling schemes (golden-angle increment or random permutations thereof) are considered. Plots of $$$f_{\rm{}S}(j)$$$ and $$$f_{\rm{}RF}(j)$$$ and RMS error data shows (in)coherency and its relationship with accuracy.

Results

Error model validation

Simulated MRF reconstructions, actual and predicted errors are displayed in Figure 2. The overall error prediction is good, even when the quantitative parameters are highly varying (e.g. bone versus CSF).

Incoherency and dependence on sequence characteristics

In Figure 3, examples of $$$f_{\rm{}S}(j)$$$ and $$$f_{\rm{}RF}(j)$$$ for golden-angle radial sampling and the smooth flip angle train of Figure 1(a) are displayed. The Fourier coefficients of $$$f_{\rm{}S}(j)$$$ have large values only at a few regularly spaced peaks, the first of which occurs some distance away from 0 (Figure 3(a)). The Fourier coefficients of $$$f_{\rm{}RF}(j)$$$ decay quickly (Figure 3(b)). This implies that the inner-product between these two functions is small consistent with the small RMS error value obtained from the corresponding reconstructions (see Table 1).

Figure 4 displays plots of $$$f_{\rm{}S}(j)$$$ and $$$f_{\rm{}RF}(j)$$$ for randomly permuted radial sampling and the non-smooth flip angle train of Figure 1(b). Using one or both of these alternative strategies leads to large inner products, which is consistent with the RMS error data.

Discussion

Acknowledgements

References

1. Ma, D. et al. Magnetic resonance fingerprinting. Nature, 495(7440):187–192, 2013.
2. Zhao, B. et al. Optimal experiment design for magnetic resonance fingerprinting: Cramer-rao bound meets spin dynamics. IEEE Trans. Med. Imaging, 2018.
3. Assländer, J. et al. Relaxation in Spherical Coordinates: Analysis and Optimization of pseudo-SSFP based MR-Fingerprinting. arXiv:1703.00481, 2017.
4. Sbrizzi, A. et al. Dictionary-free MR Fingerprinting reconstruction of balanced-GRE sequences. arXiv:1711.08905, 2017.
5. Lustig, M. et al. Compressed sensing MRI. IEEE Signal Processing Magazine, 25(2):72-82, 2008.
6. Davies, M. et al. A compressed sensing framework for magnetic resonance fingerprinting, SIAM J. Imaging Sci., 7(4): 2623-2656, 2014.
7. Kwan, R.K.-S. et al. MRI simulation-based evaluation of image-processing and classification methods, IEEE Trans. Med. Imaging, 18(11):1085-1097, 1999.