0813

Parameter Encoding Efficiency in Transient and Steady-State Quantitative MRI Methods
David Leitão1, Joseph V. Hajnal1,2, Rui P. A. G. Teixeira1, and Shaihan Malik1

1Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom

Synopsis

This work proposes a neutral measure of encoding efficiency per square-root of time excluding any effects of image reconstruction from the analysis in order to compare spoiled gradient-echo based Magnetic Resonance Fingerprinting and steady-state methods for $$$T_1$$$ and $$$T_2$$$ estimation. The results obtained indicate that gradient spoiled Fingerprinting is up to $$$50\%$$$ more efficient per square-root-time than steady-state methods. The optimal sequences of pulses found have striking features with different duration fingerprint strategies having highest efficiency under different boundary conditions.

Introduction

Magnetic Resonance Fingerprinting (MRF)$$$^{(1)}$$$ and steady-state quantitative MRI (qMRI) methods such as DESPOT$$$^{(2)}$$$ differ fundamentally in the way in which they manipulate the nuclear magnetization to encode information about relaxation times into the acquired signals. Gradient-echo based steady-state methods acquire multiple images each using different flip angles (FA) and repetition times (TR), whereas MRF uses dynamic variation during single extended acquisitions involving high undersampling, where the dynamic variation was proposed to boost the ‘encoding power’. However, differences in both signal properties and reconstruction strategies make comparing performance between these classes of methods complicated. In particular sub-optimal reconstruction from highly undersampled dynamic signals could reduce apparent MRF performance so that its true capabilities might be obscured. In this work we directly compare different pulse train strategies through their intrinsic encoding power to explore the relative merits of different approaches to qMRI. The sequence design strategies employed have much in common with other works$$$^{(3-5)}$$$.

Theory

The Cramér-Rao Lower Bound (CRLB) provides a direct means to determine the lower bound on variance for an estimated parameter $$$\theta$$$ from a set of measured data, hence an upper bound on the parameter-to-noise ratio $$$\theta NR^{(3-6)}$$$. This bound is a function of the signal-to-noise ratio (SNR) of the input data. To compare pulse sequences with different durations it is instructive to normalise to the square-root acquisition time $$$(T_{acq})$$$:

$$\theta NR_{u.t.}=\frac{\theta{}NR}{\sqrt{T_{acq}}}\equiv\eta(\theta)\cdot{}SNR_0$$

where $$$\eta (\theta)$$$ is the efficiency per square-root-time in parameter $$$\theta$$$ and $$$SNR_0$$$ is the single measurement SNR (i.e., one readout), defined with reference to maximum possible signal, $$$M_0$$$.

Methods

Sequence properties, such as spoiling, impact on encoding power, so to achieve an initial direct comparison we consider only spoiled gradient-echo (SPGR) based MRF$$$^{(7)}$$$. We investigated behaviour for fingerprints using different numbers of excitations pulses $$$(N)$$$, both starting from thermal equilibrium, and also in a driven-equilibrium (DE) case where the sequence is repeated, which may be more relevant to 3D imaging. For each case the acquisition settings $$$(\alpha_n, TR_n)$$$ were optimized by maximising the minimum $$$\eta(\theta_i=\{T_1,T_2\})$$$ subject to inequality constraints $$$g_n(TR\geq5ms,0^\circ\leq\alpha_n\leq180^\circ)$$$:

$$\mathrm{max}_{\alpha_n,TR_n}\{\mathrm{min}_i\quad\eta(\theta_i)\} $$

$$\mathrm{s.t.}\quad\quad\quad{}g_n\leq0$$

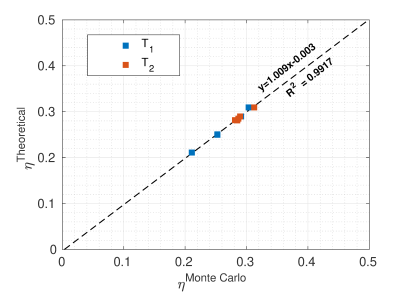
Additional optimizations used temporal smoothness (small flip angle steps) and minimum flip angle constraints proposed by Zhao$$$^{(3)}$$$. $$$\eta$$$, which has units of $$$s^{-1/2}$$$, was computed via CRLB calculations based on extended-phase-graph simulations, validated by Monte-Carlo simulations (Figure 1). All optimizations were performed for $$$\{T_1,T_2\}=\{781ms,65ms\}$$$ which approximates white matter. SS methods for mapping $$$T_1$$$ and $$$T_2$$$ require both SPGR and steady state free precession (SSFP) sequences, so that is the point of reference used.

Results

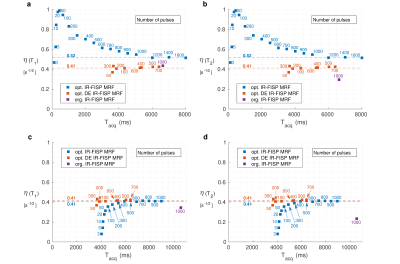
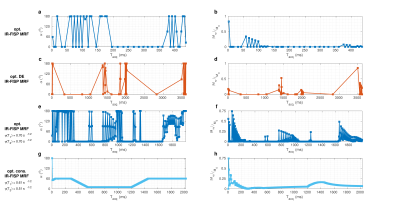
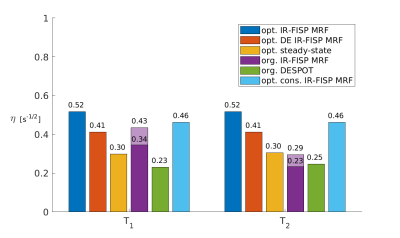
Figure 2 shows efficiency $$$\eta$$$ as a function of total acquisition time for different durations of fingerprint. If starting from thermal equilibrium (blue squares) the most efficient sequences use a small number of pulses, for example $$$N=50$$$ (figure 3a) and yield $$$\eta \approx 1$$$. The orange squares correspond to the DE version. In this case the efficiency is lower $$$(\eta \approx 0.4)$$$ and independent of $$$N$$$ (figure 3c). If the optimization is more constrained, an efficiency of $$$\eta \approx 0.5$$$ is obtained. Since optimizations starting from thermal equilibrium require periods for magnetization recovery, figure 2c/d shows how efficiency changes once an additional rest period of $$$5\times{}T_1$$$ is added – they now perform similarly to DE and shorter fingerprints are not favourable. Figure 4 shows one additional example for $$$N=10$$$. Figure 5 compares the efficiency of each method with steady-state methods$$$^{(6)}$$$.

Discussion and Conclusion

The proposed efficiency measure and subsequent optimizations yield some familiar and also unfamiliar results. For example, with $$$N=10$$$ a normal inversion recovery sequence is obtained which has relatively high efficiency $$$(\eta \approx 0.7)$$$. The highly efficient sequences found for $$$N \approx 50$$$ also include many $$$180^\circ$$$ pulses (for inversion and refocusing) and long recovery periods. In practice such short fingerprints would need to be repeated to acquire sufficient data, reducing their efficiency (fig. 1c/d). The spatial encoding method is hence important here; for 3D encoding the DE fingerprints are the most relevant. Although they have lower efficiency per unit time, 3D encoding has intrinsically higher $$$SNR_0$$$. Figure 4 suggests that MRF is intrinsically around $$$50\%$$$ more efficient per square-root time than steady-state methods, meaning that acquisition time could be halved. However, $$$\eta$$$ does not include any aspect of image encoding or reconstruction. Many optimizations returned MRF sequences with ‘zero’ flip angles, which would pose a reconstruction problem. Constraining to include a minimum flip angle reduces efficiency but not significantly. Finally, this work only considered spoiled sequences, though balanced SSFP MRF may prove significantly more efficient, being the subject of future study.

Acknowledgements

This work is funded by the King's College London & Imperial College London EPSCR Centre for Doctoral Training in Medical Imaging (EP/L015226/1).

This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.

References

$$$(1)$$$ Ma, D., Gulani, V., Seiberlich, N., Liu, K., Sunshine, J. L., Duerk, J. L., & Griswold, M. A. Magnetic resonance fingerprinting. Nature, 495(7440), 187 (2013).

$$$(2)$$$ Deoni, S. C. L., Peters, T. M. & Rutt, B. K. High-resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn. Reson. Med. 53, 237–241 (2005).

$$$(3)$$$ Zhao, B., Haldar, J. P., Setsompop, K., & Wald, L. L. Optimal experiment design for magnetic resonance fingerprinting. In Engineering in Medicine and Biology Society (EMBC), 2016 IEEE 38th Annual International Conference of the (pp. 453-456). IEEE.

$$$(4)$$$ Assländer, J., Lattanzi, R., Sodickson, D. K., & Cloos, M. A. Relaxation in Spherical Coordinates: Analysis and Optimization of pseudo-SSFP based MR-Fingerprinting. arXiv preprint arXiv:1703.00481 (2017).

$$$(5)$$$ Assländer, J.,Novikov, D. S., Lattanzi, R., Sodickson, D. K., & Cloos, M. A. Hybrid-State Free Precession in Nuclear Magnetic Resonance. arXiv preprint arXiv:1807.0342 (2018).

$$$(6)$$$ Teixeira, R. P. A., Malik, S. J., & Hajnal, J. V. Joint system relaxometry (JSR) and Crámer‐Rao lower bound optimization of sequence parameters: A framework for enhanced precision of DESPOT T1 and T2 estimation. Magnetic resonance in medicine, 79(1), 234-245.(2018).

$$$(7)$$$ Jiang, Y., Ma, D., Seiberlich, N., Gulani, V., & Griswold, M. A. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magnetic resonance in medicine, 74(6), 1621-1631.(2015).

Figures

Figure 1 - Comparison of the theoretical efficiency computed via Cramér-Rao Lower Bound calculation, and Monte Carlo experiment using least squares fitting. There is a very good agreement between the two measures.

Figure 2 - Efficiency of spoiled gradient-echo MRF for $$$T_1$$$ (a,c) and $$$T_2$$$ (b,d) encoding for different duration fingerprints. The ‘original’ published sequence$$$^{(7)}$$$ is shown in purple. From the top to the bottom row, a relaxation period of $$$5\times{}T_1$$$ is added to ‘opt. IR-FISP MRF’ such the magnetization returns to thermal equilibrium, allowing to repeat the sequence in a 3D experiment. Note that the driven-equilibrium (DE) version does not need such a relaxation period because it runs in a loop as many times as necessary.

Figure 3 - Optimal acquisition settings (left column) and respective signal (right column) for some example optimized fingerprint sequences. (a,b) IR-FISP with $$$N=50$$$ pulses/readouts; (c,d) Driven-Equilibrium (DE) with $$$N=50$$$ pulses/readouts; (e,f) IR-FISP with $$$N=400$$$; (g,h) Constrained IR-FISP with $$$N=400$$$.

Figure 4 - Example of an optimized fingerprint for $$$N=10$$$, optimized only for efficiency of $$$T_1$$$ estimation. This turns out to be a classic inversion recovery sequence. The optimization determines that it is more effective to allow magnetization to recover than to acquire more signals in the period between first and last pulse.

Figure 5 - Average efficiency for different techniques. The pale bar represents the gain in encoding efficiency of a single run compared to adding a relaxation period to allow repeating the sequence for a 3D experiment. For the case of ‘opt. IR-FISP MRF’ only the average efficiency for a prolonged single run is shown as it was the best-case scenario. The ‘opt. cons. IR-FISP MRF’ is the efficiency of the prolonged MRF when constraining the acquisition settings like Bo Zhao et al.$$$^{(3)}$$$.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)
0813