0557

Non-negative mean apparent propagators using sum-of-squares optimization: MAP+

Tom Dela Haije¹, Evren Özarslan², and Aasa Feragen¹

¹University of Copenhagen, Copenhagen, Denmark, ²Linköping University, Linköping, Sweden

Synopsis

Mean apparent propagator (MAP) MRI provides an efficient representation of the three-dimensional q-space signal that is used to characterize the diffusional characteristics of the tissue. The standard implementation of MAP-MRI imposes soft constraints, leaving the possibility for negative values of the propagator; we observed that such physically unjustifiable reconstructions are widespread throughout the brain. Here, we introduce a new framework based on sum-of-squares optimization that guarantees the non-negativity of the reconstructed propagator, thus yielding improved estimates of the propagator as well as the scalar measures derived from it.

Introduction

The mean apparent propagator (MAP)¹⁰ MRI technique employs a computationally efficient basis for diffusion-weighted MRI data that enables the reconstruction of the full diffusion propagator, and is being increasingly used to study diffusion characteristics within the brain. A valid set of reconstructed MAP parameters corresponds to a physically plausible, globally non-negative propagator, which all current implementations encourage by enforcing non-negativity constraints in a finite set of points. In this work, we show that such soft constraints are generally insufficient, and result in estimation biases that can exceed variations due to the investigated process (e.g. development, aging) or pathology in group studies. To prevent such biases, we propose a new set of constraints for MAP-MRI that guarantee non-negativity of the propagator globally, based on sum-of-squares constraints that have previously been applied successfully to the cumulant expansion². The use of these stricter constraints should increase the reliability of MAP-MRI-derived measures in clinical studies.

Methods

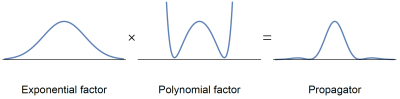
The propagator associated with a MAP fit is given by the product of an exponential factor, typically constructed to correspond to the expected Gaussian behavior described by e.g. DTI, and a polynomial factor that corrects for non-Gaussian effects, cf. Fig. 1. Because the exponential factor is guaranteed to be positive everywhere, non-negativity of the propagator is entirely determined by the polynomial factor. To ensure non-negativity of this polynomial factor—and thus of the entire mean apparent propagator—we propose to use sum-of-squares optimization⁵.

The central idea behind sum-of-squares optimization is that non-negativity of a polynomial is trivially guaranteed if it can be written as a sum of squared polynomials. Thanks to the denseness results of Lassere⁴ we know that these sum-of-squares constraints are a practically useful substitute for the general non-negativity constraint, and the works of Parrilo⁵ and others then show that these constraints can be verified and imposed in practice using semidefinite programming¹. In the following experiments we use the semidefinite programming solver SDPA⁹ (default settings) to validate the sum-of-squares condition on the even order $$$K$$$ polynomial factor

$$\sum_{k=0,2,\ldots,K} \, \sum_{n_1 + n_2 + n_3 = k} \frac{a_{n_1 n_2 n_3}}{\sqrt{2^k \, n_1! n_2! n_3!}} H_{n_1}(r_1) H_{n_2}(r_2) H_{n_3}(r_3),$$

where $$$a_{n_1 n_2 n_3}$$$ are the parameters, $$$n_1$$$, $$$n_2$$$, and $$$n_3$$$ are non-negative integers, and $$$H_n$$$ is the $$$n$$$^th order Hermite polynomial. We do this for an entirely unconstrained MAP reconstruction and for the soft constrained (standard) MAP implementation provided by the TORTOISE 3.1.3 package^3,6, computed for a subject in the MGH HCP^7,8 adult diffusion database. This data set has $$$1.5 \, \mathrm{mm}$$$ isotropic voxels, and $$$b = \{1, 3, 5, 10\} \, \textrm{ms}/\mu\textrm{m}^2$$$ shells with $$$\{64, 64, 128, 256\}$$$ measurements respectively, as well as $$$10$$$ $$$b = 0 \, \textrm{ms}/\mu\textrm{m}^2$$$ images. To distinguish between the soft constrained implementation and our strict sum-of-squares constrained implementation, we will refer to the latter as MAP+. The integral probability constraint¹⁰ that is typically included in MAP is obsolete in MAP+ and can be omitted. For the considered orders, the running time for our current implementation of MAP+ is comparable to that of standard MAP.

Results

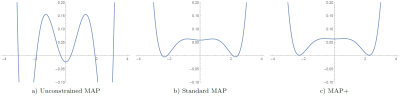
We illustrate the advantage of MAP+ over standard MAP in Fig. 2, where we also compare MAP+ to an entirely unconstrained reconstruction of the propagator. Of the three reconstruction algorithms, only MAP+ produces a polynomial factor / propagator that is non-negative everywhere. Despite their seemingly enormous differences, the difference in the residuals between MAP+ and unconstrained MAP is only a few percent, so the fits are of comparable quality.

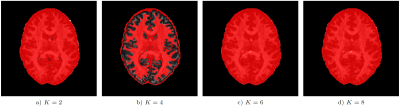
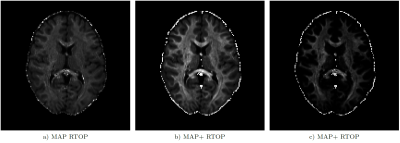
Analysis of the full data set shows that global non-negativity of the propagator is violated in large portions of the image data. Fig. 3 shows the location of these constraint violations in an axial slice, where we identified propagators with negative regions in $$$99.4 \%$$$ ($$$K=2$$$), $$$57.1 \%$$$ ($$$K=4$$$), $$$99.8 \%$$$ ($$$K=6$$$), and $$$99.8 \%$$$ ($$$K=8$$$) of the voxels inside the brain mask ($$$439 248$$$ voxels). The polynomial factor plots in Fig. 4 give some insight into the cause of the observed percentages. We finally note that these violations can have a significant effect on commonly used scalar measures, cf. Fig.5.

Conclusion

Preliminary results on a single data set suggest that the usual constraints for MAP-MRI are quite insufficient—independent of the maximum model order we observed violated constraints in nearly $$$100 \%$$$ of white matter voxels. The resulting bias depends on the specific application but can be significant—the proposed MAP+ approach using sum-of-squares constraints completely nullifies this bias. The computational cost of the MAP+ method is currently being investigated, but is expected to be comparable to the standard MAP approach.

Acknowledgements

The authors gratefully acknowledge the Villum Foundation for financial support. Data were provided in part by the McDonnell Center for Systems Neuroscience at Washington University, and by the Human Connectome Project, MGH-USC Consortium (Principal Investigators: Bruce R. Rosen, Arthur W. Toga and Van Wedeen; U01MH093765) funded by the NIH Blueprint Initiative for Neuroscience Research grant; the National Institutes of Health grant P41EB015896; and the Instrumentation Grants S10RR023043, 1S10RR023401, 1S10RR019307.

References

[1] S. P. Boyd et al. Convex optimization. 2004.

[2] T. C. J. Dela Haije et al. "The importance of constraints and spherical sampling in diffusion MRI". In: Proceedings of the 26th Annual Meeting of the ISMRM. 2018, p. 5335.

[3] M. O. Irfanoglu et al. "TORTOISE v3: Improvements and new features of the NIH diffusion MRI processing pipeline". In: Proceedings of the 25th Annual Meeting of the ISMRM. 2017, p. 3540.

[4] J. B. Lasserre. "A sum of squares approximation of nonnegative polynomials". In: SIAM Review 49.4 (2007), pp. 651-669.

[5] P. A. Parrilo. "Semidefinite programming relaxations for semialgebraic problems". In: Mathematical Programming 96.2 (2003), pp. 293-320.

[6] C. Pierpaoli et al. "TORTOISE: An integrated software package for processing of diffusion MRI data". en. In: Proceedings of the 18th Annual Meeting of the ISMRM. 2010, p. 1597.

[7] K. Setsompop et al. "Pushing the limits of in vivo diffusion MRI for the Human Connectome Project". In: NeuroImage80 (2013), pp. 220-233.

[8] D.C. Van Essen et al. "The Human Connectome Project: A data acquisition perspective". In: NeuroImage 62.4 (2012),pp. 2222-2231.

[9] M. Yamashita et al. A high-performance software package for semidefinite programs: SDPA 7. Research Report B-460. Tokyo Institute of Technology, 2010.

[10] E. Özarslan et al. "Mean apparent propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure". In: NeuroImage 78 (2013), pp. 16-32.

[11] E. Özarslan et al. "Simple harmonic oscillator based reconstruction and estimation for one-dimensional q-space magnetic resonance (1D-SHORE)". In: Excursions in Harmonic Analysis, Volume 2. 2013, 373-399.

Figures

A small schematic illustrating the functional form of the mean apparent propagator, consisting of a product of an exponential factor that describes the Gaussian part of the observed diffusion, and a polynomial factor that corrects for non-Gaussian effects. As the Gaussian part is obtained from a properly constrained fit, it is guaranteed to be non-negative. Non-negativity of the propagator is thus entirely determined by the non-negativity of the polynomial factor, which is attained here using sum-of-squares optimization.

Plots of the polynomial factor in the mean apparent propagator ($$$K=6$$$) estimated using increasingly strict constraints, plotted along one axis (in local coordinates) in a voxel of the marmoset data used in the original MAP-MRI paper by Özarslan et al. a) Unconstrained MAP-MRI does not produce a reasonable propagator. b) The standard approach to estimating the MAP parameters enforces non-negativity in a finite set of points in the neighborhood of the origin, and consequently produces a polynomial that corresponds to a much more plausible propagator. c) The polynomial reconstructed with MAP+ is the only one that is globally non-negative.

A fractional anisotropy image of an axial slice in the MGH HCP data set, with highlighted in red those voxels where the standard MAP implementation of TORTOISE fails to produce a strictly non-negative propagator. The soft constraints enforced in the standard reconstruction of MAP are insufficient in white matter independent of the order $$$K$$$, and insufficient everywhere for $$$K \neq 4$$$.

Plots of the polynomial factor for different orders $$$K$$$, computed for a random voxel in the HCP data set. In the limit where gradient strength goes to infinity, the polynomial factors in the particular case $$$K=4$$$ naturally tend to veer off to plus infinity. The standard localized constraints appear sufficient to then keep the behavior of the propagator near the origin under control, which could be one possible explanation for the drop in the number of violated constraints observed for $$$K=4$$$ in Fig. 3.

The return to origin probability (RTOP) is a typical diffusion measure used in analysis pipelines based on MAP-MRI. Shown here are RTOP maps computed using a) MAP and b) MAP+; the values range from $$$0 \,\mu\mathrm{m}^{-3}$$$ (dark) to $$$0.113 \, \mu\mathrm{m}^{-3}$$$. We find significant differences between the two reconstructions, which are concentrated mainly in the white matter. A map of the absolute differences is shown in c).

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

0557