0474

Leveraging conditional GANs with adaptive loss balancing for MRI sparse reconstruction.
Itzik Malkiel1, Sangtae ahn2, Valentina Taviani3, Anne Menini3, Zachary Slavens4, and Christopher Hardy2

1GE Global Research, Herzliya, Israel, 2GE Global Research, Niskayuna, NY, United States, 3GE Healthcare, Menlo Park, CA, United States, 4GE Healthcare, Waukesha, WI, United States

Synopsis

We propose a Conditional Wasserstein Generative Adversarial Network (cWGAN), trained with a novel Adaptive Loss Balancing (ALB) technique that stabilizes the training and minimizes the presence of artifacts, while maintaining a high-quality reconstruction with more natural appearance (compared to non-GAN techniques). Multi-channel 2D brain data with fourfold undersampling were used as inputs, and the corresponding fully-sampled reconstructed images as references for training. The algorithm produced higher-quality images than state-of-the-art deep learning-based models in terms of perceptual quality and realistic appearance.

PURPOSE

Recent MRI sparse reconstruction models use deep neural networks to reconstruct high-quality images from highly undersampled k-space data. However, these techniques sometimes struggle to reconstruct sharp images that preserve fine details while maintaining a natural appearance. In this context, Generative Adversarial Networks (GAN)1 are known for their ability to generate high-quality natural images from a given noise or image input, and have been used for sparse MRI reconstruction2-4. Nonetheless, GANs generally suffer from instabilities during training, and when applied to smaller-sized datasets, can generate image artifacts, which are especially problematic in a radiological setting. We propose a Conditional Wasserstein Generative Adversarial Network (cWGAN), trained with a novel Adaptive Loss Balancing (ALB) technique that stabilizes the training and minimizes the presence of artifacts, while maintaining a high-quality reconstruction with image texture closer to that of the fully-sampled images. We compare various types of GAN models, showing that ALB training improves model performance and accelerates convergence.

METHODS

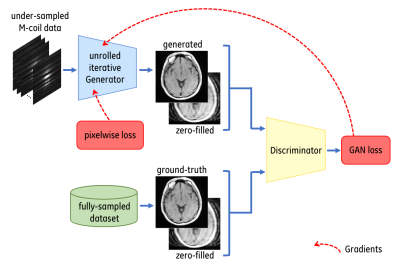
Following the success of conditional GANs (cGAN)5 and WGANs6, we apply a cWGAN technique for an MRI sparse reconstruction (MRI-SR) model. Our model combines a generator network and a discriminator network that are being trained against each other. The generator is trained to reconstruct a fully-sampled image from a given under-sampled k-space dataset, that will minimize the approximated Earth Moving Distance (EMD) estimated by the critic (discriminator) and a pixel-wise loss. The critic receives either 1) pairs of zero-filled and generated images or 2) pairs of zero-filled and fully-sampled images and learns to estimate the EMD between the former (fake pairs) and the later (real pairs).

During traditional GAN training, the GAN loss may generate gradients with variable norm. To stabilize the GAN training and to avoid drifting away from the ground-truth spatial information, we use ALB that balances the GAN loss with the pixel-wise loss. ALB insures that the standard deviation (SD) of the GAN loss gradients will be upper-bounded by a ratio with the SD of the pixel-wise loss gradients. Our cWGAN-ALB model uses a cGAN architecture (Fig. 1) trained with ALB and WGAN objective (Fig. 2), where the generator architecture is a DCI-Net7 with 20 iterations and our critic architecture is based on the discriminator from DCGAN8.

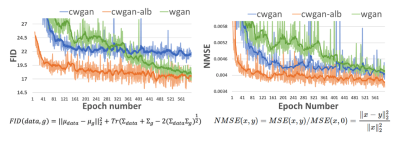
Fréchet Inception Distance (FID)9 is a similarity measure between two datasets that correlates well with human judgement of visual quality, and is most often used to evaluate the quality of images generated by GANs10. We utilize FID as a quality metric to evaluate the similarity between the set of our generated images and the corresponding fully-sampled images. FID relies on the Fréchet distance calculated from two Gaussians each fitted on feature vectors taken from a pre-trained Inception network11, one for the generated images and one for the fully-sampled images. To our knowledge, we are the first to utilize FID for measuring image quality of MRI-SR models.

RESULTS

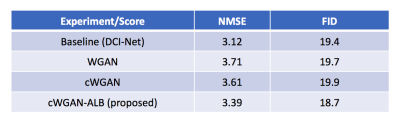
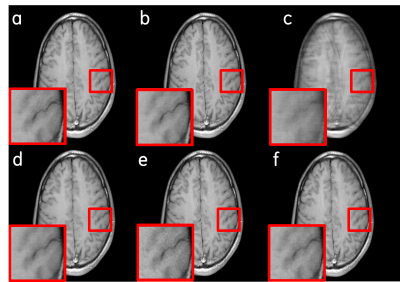
We compared (Figs. 3, 4) our cWGAN-ALB with three other models: 1) cWGAN, 2) WGAN, and 3) a baseline MRI-SR model without any GAN technique. All models were evaluated with Normalized MSE (NMSE) and FID. We found that (a) cWGAN and cWGAN-ALB have better SNR and fewer artifacts than WGAN, (b) cWGAN-ALB converges much faster than cWGAN and WGAN and performs better in both FID and NMSE measures (Table 1) and (c) although cWGAN-ALB has higher NMSE than the baseline model, it performs better in FID and yields sharper images with more fine details while maintaining a more natural image texture.

DISCUSSION

While it is possible to use a non-conditional GAN architecture, it is likely that for a given under-sampled k-space dataset, the generator will reconstruct a fairly realistic image, but since a non-conditional critic sees only the reconstructed image, it is not guaranteed that the generator will learn to reconstruct a realistic image that perceptually matches the given zero-filled image. In other words, a non-conditional critic is only able to learn general properties of the appearance of the entire distribution, however it’s not likely to perfectly match a specific sample.

Our proposed cWGAN-ALB model has three advantages over a conventional GAN: 1) A critic that receives both the input image and the reconstructed image is able to enforce higher data fidelity compared to a non-conditional GAN architecture; 2) Its training leads to perceptually better appearance of the reconstructed images; and 3) It stabilizes the training and leads to better convergence.

CONCLUSION

In this work we design, train and test a MRI-SR model using cWGAN technique and a novel GAN training algorithm, showing a capability for generating sharper images with more fine details and natural appearance, by leveraging GANs properly. This work enables sparser sampling and thus higher clinical imaging speeds.

Acknowledgements

References

1. Goodfellow I, et al. Generative adversarial nets. Advances in neural information processing systems. 2014.

2. Mardani M, Gong E, Cheng JY, et al. Deep generative adversarial networks for compressed sensing (GANCS) automates MRI. arXiv preprint arXiv:1706.00051 (2017).

3. Yang G, Yu S, Dong H, et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for fast compressed sensing MRI reconstruction. IEEE Trans Med Imag 2018;37:1310-1321.

4. Hammernik K, Kobler E, Pock T, et al. Variational adversarial networks for accelerated MR image reconstruction. International Society for Magnetic Resonance in Medicine 26th Annual Meeting, June 16 - 21, 2018, Paris, p. 1091.

5. Mirza M, Osindero S. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014).

6. Arjovsky M, Chintala S, Bottou L. Wasserstein GAN. arXiv preprint arXiv:1701.07875 (2017).

7. Malkiel I, Ahn S, Slavens Z, Taviani V, Hardy CJ. Densely-connected iterative network for sparse MRI reconstruction. International Society for Magnetic Resonance in Medicine 26th Annual Meeting, June 16 - 21, 2018, Paris, p. 3363.

8. Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434 (2015).

9. Karras T, Aila T, Laine S, Lehtinen J. Progressive growing of GANs for improved quality, stability, and variation. arXiv preprint arXiv:1710.10196 (2017).

10. Heusel M, Ramsauer H, Unterthiner T, Nessler B. GANs trained by a two time-scale update rule converge to a local Nash equilibrium. Advances in Neural Information Processing Systems. 2017.

11. Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition. 2015.

Figures

Figure 1. The generator receives under-sampled k-space data as input and generates a matched estimated fully sampled image. The generator loss function incorporates a weighted sum of a pixel-wise distance (MSE) and a GAN loss, and its architecture is based on an unrolled iterative network of 20 iterations, each containing data-consistency and regularization blocks with dense connections between iterations6. The critic learns to estimate the EMD between “fake” pairs of zero-filled and generated images, and “real” pairs of zero-filled and fully-sampled images. Our critic architecture relies on the discriminator from DCGAN7.

Figure 2. Our WGAN-ALB training. Adopting the training algorithm of WGAN, we calculate two moving-average variables for the SD of both pixel-wise and GAN loss gradients. Every training step, if the cumulative SD of the GAN gradients is greater than the cumulative SD of the pixel-wise gradients, we increase β which carefully decays the GAN loss gradients to the same order of magnitude as those of the pixel-wise loss. Moreover, in order to keep a reasonable ratio between the generator’s GAN gradients and the discriminator’s gradients, we also decay the discriminator loss by the same factor.

Figure 3. A comparison of WGAN, cWGAN and cWGAN-ALB on the validation set. We calculated the FID and the average normalized mean-square error (NMSE) for every epoch during the training. The conditional WGAN converges better in terms of NMSE, compared to a WGAN (without condition). In addition, our proposed model with ALB converges faster and reaches significantly better performance for both NMSE and FID.

Table 1. Evaluation on a holdout test set. Our proposed model outperforms other GAN based models according to both scores, and results in better FID compared to the baseline model. Although cWGAN-ALB exhibits slightly degraded NMSE performance compared to the baseline, it generates images with higher visual quality, while the baseline sometimes exhibits some blurring (see Fig. 4). Note that our baseline model uses a similar generator architecture and was trained without any GAN technique, for roughly twice the number of epochs (compared to the GAN models).

Figure 4. A representative example with ROIs showing the reconstruction of all models side-by-side: a) cWGAN-ALB; b) ground-truth (fully-sampled) image; c) zero-filled image; d) baseline generator network; e) WGAN; f) cWGAN. cWGAN and cWGAN-ALB have better SNR and fewer artifacts than WGAN. cWGAN-ALB yields sharper images with more fine details while maintaining a more natural appearance. The baseline model sometimes exhibits some blurring.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)
0474