0427
Steady-state imaging with “inhomogeneous” MT contrast1Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom
Synopsis
A matrix-based framework for modelling of inhomogeneous MT effects was developed for steady-state gradient echo sequences. This was applied to sequences using multi-band pulses that are designed to create some off-resonance saturation simultaneously with excitation of free water. Simulations and phantom results show that ihMT contrast can be achieved in this way, and in-vivo results show the expected strong white-matter contrast.
Introduction
The recently introduced ‘inhomogeneous’ (aka ‘dipolar’) magnetization transfer (ihMT) contrast mechanism1 is a new method for generating MT contrast that appears to be more specific to myelinated tissue, and hence could be an important mechanism for neuroimaging. The purpose of this work is to investigate ihMT contrast in steady-state gradient echo sequences using constant saturation2 multiband excitation pulses.Theory
In a system with free (f) water and semisolid (s) protons with some dipolar order, the magnetization vector may be written as $$$ \mathbf{M}=\begin{pmatrix}M_+^f&M_-^f&M_z^f&M_{Z}^s&M_{D}^s\end{pmatrix}^T$$$ where $$$M_\pm^f=M_x^f\pm\,iM_y^f$$$. The semisolid pool now contains two compartments3 representing the ‘Zeeman’ (Z) and ‘Dipolar’ (D) ordered magnetization. $$$M_Z^s$$$ is usually used to characterise MT effects; $$$M_D^s$$$ represents dipolar spin order, here represented by a dimensionless polarization term4. The system evolves according to the following expression:$$\frac{d\mathbf{M}}{dt} = \mathbf{\left(\Omega+\Lambda\right)M+C}$$ where $$\mathbf{\Omega}=\begin{pmatrix}\mathbf{\Omega_{free}}&\begin{matrix}0&0\\0&0\\0&0\end{matrix}\\\begin{matrix}0&0&0\\0&0&0\end{matrix}&\mathbf{\Omega_{semi}}\end{pmatrix} \ \mathbf{\Lambda}=\begin{pmatrix}-R_2^f-i\delta\omega&0&0&0&0\\0&-R_2^f+i\delta\omega&0&0&0\\0&0&-KM_0^s-R_1^f&KM_0^f&0\\0&0&KM_0^s&-KM_0^f-R_{1Z}^s&0\\0&0&0&0&-R_{1D}^s\end{pmatrix}$$ $$\mathbf{C}=\begin{pmatrix}0\\0\\R_1^fM_0^f\\R_{1Z}^sM_{0}^s\\0\end{pmatrix}$$. Matrix $$$\Lambda$$$ describes free pool precession, relaxation of all pools (semisolid pool has separate R1 for Zeeman and Dipolar terms) and exchange of longitudinal magnetization between free and semisolid pools, usually used to describe MT effects. $$$\mathbf{\Omega}$$$ describes RF effects, subdivided into $$ \mathbf{\Omega_{semi}} = \sum_{\Delta}\begin{pmatrix}-W(\Delta)&W(\Delta)\frac{\Delta}{\omega_{loc}}\\W(\Delta)\frac{\Delta}{\omega_{loc}}&-W(\Delta)\left(\frac{\Delta}{\omega_{loc}}\right)^2\end{pmatrix} \ \mathbf{\Omega_{free}} = \begin{pmatrix}0&0&i\omega_{1+}\\0&0&-i\omega_{1+}^{*}\\\frac{i}{2}\omega_{1+}^{*}&-\frac{i}{2}\omega_{1+}&0\end{pmatrix}$$ where $$$\Omega_{free}$$$ is the Bloch equation for the free pool in this basis ($$$\omega_{1+}=\gamma(B_{1,x}+iB_{1,y}$$$) and $$$\Omega_{semi}$$$ describes energy absorption by the semisolid pools. RF with off-resonance frequency $$$\Delta$$$ is absorbed by the system at rate $$$W(\Delta)=\pi|\omega_{1+}|^2g(\Delta)$$$ where $$$g(\Delta)$$$ is the absorption lineshape. The first element of $$$\Omega_{semi}$$$ is classically used for modelling MT effects5. Provotorov theory adds that off-resonance irradiation drives mixing between semisolid and Zeeman pools (off-diagonal elements); here $$$\omega_{loc}$$$ is the strength of local field fluctuations (related to $$$g(\Delta)$$$).For multiband RF $$$\Omega_{semi}$$$ is a sum over off-resonance bands; this assumption is valid as long as the bands are narrow wrt g and $$$\Delta\gg\omega_1$$$.
There are a few properties to note for sequence modelling: (i) exchange between $$$M_Z^{s}$$$ and $$$M_D^{s}$$$ is purely RF driven, while exchange between $$$M_z^{f}$$$ and $$$M_Z^{s}$$$ occurs continuously; (ii) coupling terms in $$$\Omega_{semi}$$$ are linear in $$$\Delta$$$, so equal off-resonance RF power applied at $$$\pm\Delta$$$ (or on-resonance) eliminates mixing between semisolid pools; (iii) $$$M_D^{s}$$$ relaxes to a thermal equilibrium value of zero.
Methods
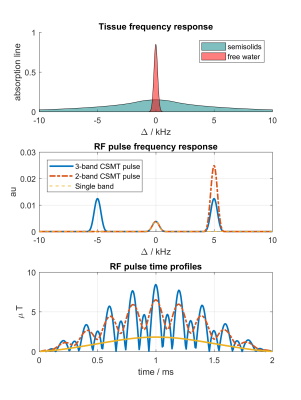
Following the CSMT framework2, we use 3D imaging sequences along with multiband RF pulses with no underlying selection gradient. Hence the central band excites free water while all bands solely affect semisolid protons (Figure 1). It was previously shown that this approach can be used to stabilize variable-flip-angle relaxometry by equalizing MT effects across experiments. If ihMT effects are now included we may write the steady state magnetization for a balanced-SSFP sequence as: $$\mathbf{M^{SS}=\left(\Phi-TS\right)^{-1}T\left(S-1\right)\Lambda^{-1}C}$$
and for spoiled-gradient-echo (SPGR) as: $$\mathbf{M^{SS}=\left(1-T\Xi\,S\right)^{-1}T\Xi\left(S-1\right)\Lambda^{-1}C}$$ where $$$\mathbf{T}\equiv\exp{\mathbf{\Omega}\tau}$$$, $$$\mathbf{S}\equiv\exp{\mathbf{\Lambda}TR}$$$, $$$\mathbf{\Phi}=diag(-1\,-1\,1\,1\,1)$$$ accounts for bSSFP phase cycling and $$$\mathbf{\Xi}=diag(0\,0\,1\,1\,1)$$$ accounts for SPGR spoiling. Note here we use the pulsed formalism5 in which $$$\Omega_{semi}$$$ is treated as constant during an RF pulse with $$$\omega_{1+}$$$ replaced by $$$\omega_{1+}^{RMS}$$$.
These formulae were used to simulate the expected signal curves for white matter using parameters from by Mchinda et al6. Multiband pulses with 2 and 3 bands were employed; 2-band pulses include one off-resonance band, so couple $$$M_Z^{semi}$$$ and $$$M_D^{semi}$$$, whereas 3-band pulses are symmetric and lead to no coupling. We also performed an experiment using doped water (no MT effect), bovine serum albumin (BSA; classic MT effect only), and hair conditioner, which has been shown to exhibit strong ihMT contrast7. Finally, a bSSFP scan using B1rms=4.7uT with 2 and 3-band pulses was run on a single volunteer at1.5T (flip=25°,TR=5ms,$$$\tau=2ms$$$,$$$\Delta=8kHz$$$,1.5mm3 isotropic resolution).
Results
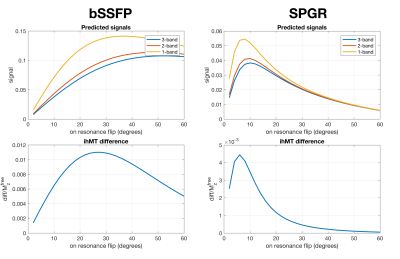
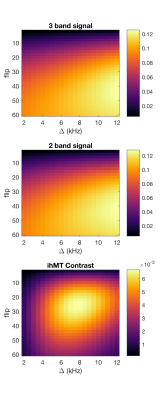
Figure 2 shows that 2- and 3-band sequences will produce different signal profiles for both SSFP and SPGR; 2-band pulses which mix Zeeman and dipolar orders will lead to higher signal. Figure 3 shows (for bSSFP) that this ihMT contrast varies also with $$$\Delta$$$, but that a maximum occurs at around 8kHz. Figure 4 shows phantom imaging results confirming these predictions qualitatively: in water and in BSA no ihMT contrast is seen, whereas hair conditioner shows the expected contrast. Figure 5 shows in-vivo results indicating stronger ihMT contrast in white matter, as would be expected.Discussion/Conclusion
We have demonstrated how to incorporate dipolar ordered magnetization into a simple matrix calculation to examine ihMT contrast. Experimentally measured signals follow the expected relationships (2-band pulses give higher steady-state signal) and an in-vivo ihMT-weighted image was formed using bSSFP with multiband pulses. Other work6 has focused on using preparation modules to generate ihMT contrast; in this work we have instead used multiband excitation pulses themselves to do this within rapid sequences. In future a combined approach may yield optimal sensitivity.Acknowledgements
This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.References
- Girard, O. M. et al. Magnetization transfer from inhomogeneously broadened lines (ihMT): Experimental optimization of saturation parameters for human brain imaging at 1.5 Tesla. Magn. Reson. Med. 2121, 1–11 (2014).
- A.G. Teixeira, R. P., Malik, S. J. & Hajnal, J. V. Fast quantitative MRI using controlled saturation magnetization transfer. Magn. Reson. Med. 1–14 (2018). doi:10.1002/mrm.27442
- Varma, G. et al. Interpretation of magnetization transfer from inhomogeneously broadened lines (ihMT) in tissues as a dipolar order effect within motion restricted molecules. J. Magn. Reson. 260, 67–76 (2015).
- Lee, J. S., Khitrin, A. K., Regatte, R. R. & Jerschow, A. Uniform saturation of a strongly coupled spin system by two-frequency irradiation. J. Chem. Phys. 134, 1–6 (2011).
- Graham, S. J. & Henkelman, R. M. Understanding pulsed magnetization transfer. J. Magn. Reson. Imaging 7, 903–912 (1997).
- Mchinda, S. et al. Whole brain inhomogeneous magnetization transfer (ihMT) imaging: Sensitivity enhancement within a steady-state gradient echo sequence. Magn. Reson. Med. 00, (2017).
- Varma, G. et al. In vivo measurement of a new source of contrast, the dipolar relaxation time, T1D, using a modified inhomogeneous magnetization transfer (ihMT) sequence. Magn. Reson. Med. 78, 1362–1372 (2017).
Figures