0308

Three-Dimensional Whole Brain Simultaneous T1, T2, and Apparent Diffusion Coefficient Mapping Using MR Multitasking

Sen Ma^1,2, Anthony G Christodoulou², Christopher T Nguyen^2,3, Fei Han⁴, Nan Wang^1,2, Yibin Xie², and Debiao Li^1,2

¹Department of Bioengineering, University of California, Los Angeles, Los Angeles, CA, United States, ²Biomedical Imaging Research Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, ³Cardiovascular Research Center, Massachusetts General Hospital and Harvard Medical School, Charlestown, MA, United States, ⁴Siemens Healthcare, Los Angeles, CA, United States

Synopsis

Three-dimensional, multi-parametric quantitative mapping of relaxation and diffusion parameters is desirable for many clinical imaging application, including the diagnosis and follow-up assessment of tumors. Traditionally, this is performed by separate scans which are time-consuming. We propose a novel Multitasking framework to achieve 3D whole-brain simultaneous T1/T2/ADC mapping in ~9min. The underlying multidimensional image is modeled as a low-rank tensor, with a time-resolved phase correction technique to compensate for the phase inconsistency induced by pulsatile motion during diffusion preparation. T1/T2/ADC measurements in healthy volunteers agree with reference methods, yielding intraclass correlation coefficients > 0.80 for both gray and white matter.

Introduction

Quantitative multiparametric mapping of relaxation and diffusion parameters is promising for clinical diagnosis of brain, breast, prostate diseases, and more^1-3. This is typically performed in separate scans, which is challenging in clinical application due to long scan times. Clinical diffusion-weighted imaging usually adopts single-shot multi-slice EPI acquisition due to the difficulty of correcting for phase inconsistencies between shots, which frequently results in image distortion and mis-registration. Joint T1/T2 mapping has been achieved using MR fingerprinting⁴, while joint T1/T2/ADC mapping has also been proposed but is subject to impractically prolonged scan time or incomplete ADC quantification^5,6. We propose a novel method for 3D whole-brain simultaneous T1/T2/ADC mapping using the recently developed Multitasking framework to model the multidimensional image as a low-rank tensor (LRT)⁷. We augment this framework by incorporating a novel time-resolved phase correction to compensate for the shot-to-shot phase variation due to pulsatile motion. Quantification of T1/T2/ADC is evaluated on phantom and healthy volunteers.

Methods

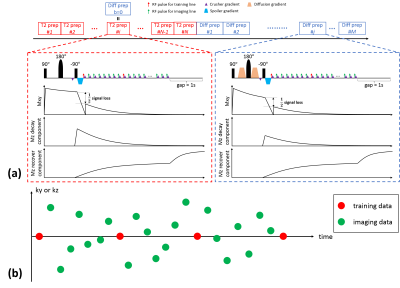
Sequence Design: T1-T2-diffusion weighting was generated using hybrid T2- and diffusion-preparation (Fig. 1a). A crusher gradient scheme was implemented to prevent the inconsistent phase from being tipped into magnitude at the cost of half signal loss^8,9, yielding a T1-decay signal evolution which was sampled using FLASH readouts (flip angle=5, TR/TE=5.6/2.5ms). An 1s gap was placed at the end of each shot to allow long-T1 tissues to recover towards thermal equilibrium. Imaging data ( $\mathbf{d}_\text{img}$ ) were sampled with Gaussian variable density along ky and kz, while training data ( $\mathbf{d}_\text{tr}$ ) were sampled every 8 readouts at k-space center (Fig. 1b). The resulting signal equation is:where $A$ absorbs proton density and T2* weighting, $n$ is the readout index, and $\alpha$ denotes FLASH flip angle.

Reconstruction: The multidimensional image can be represented as a 5-way tensor $\mathcal{A}$ with one dimension indexing voxel location $\mathbf{r}=(x,y,z)$ and four indexing different time/parameter dimensions: T1 decay $t_{\text{T1}}$ , T2prep duration $t_{\text{T2}}$ , b-value $t_{\text{b}}$ , and diffusion direction $t_{\text{dir}}$ . A time-resolved phase map $\mathbf{P}$ is applied to compensate for shot-to-shot phase inconsistency, restoring spatiotemporal image correlation thus lowering the effective tensor rank. We express this phase-corrected LRT model as $\mathbf{A}_{(1)}=\mathbf{P}\circ (\mathbf{U\Phi})$ where $\mathbf{A}_{(1)}$ is the unfolded matrix form of $\mathcal{A}$ , $\mathbf{U}$ contains spatial coefficient maps, and $\mathbf{\Phi}$ contains multidimensional temporal basis functions characterizing the four temporal dimensions¹⁰. $\mathbf{P}$ is estimated from a real-time reconstruction: $\mathbf{P}=\angle S(\mathbf{I}_{0}),\: \text{with}\: \mathbf{I}_{0}=\mathbf{U}_{0}\mathbf{\Phi}_{0,\text{rt}},\: \text{where}\: \mathbf{U}_{0}=\underset{\mathbf{U}}{\text{argmin}}\left \| \mathbf{d}_{\text{img}}-E(\mathbf{U}\mathbf{\Phi}_{0,\text{rt}}) \right \|^{2},$ where the real-time temporal subspace $\mathbf{\Phi}_{0,\text{rt}}$ is estimated from SVD of $\mathbf{d}_{\text{tr}}$ , $E(\cdot )$ combines spatial encoding and sampling, and $S(\cdot )$ performs smoothing. $\mathbf{\Phi}$ is determined via Bloch-constrained LRT completion and high-order SVD⁷ of the multidimensional tensor subspace. $\mathbf{U}$ is recovered by mapping the spatial coefficient maps from the phase-varying real-time subspace to the phase-corrected multidimensional subspace via applying the time-resolved $\mathbf{P}$ and projection operator.

Experiment Design: Data were collected on a 3T Siemens Vida scanner on an ISMRM/NIST system phantom and $n$ =4 healthy volunteers. The imaging protocol included: 1) IR-TSE for T1 reference; 2) Multiecho-SE for T2 reference; 3) Single-shot EPI for ADC reference; 4) T1/T2/ADC Multitasking sequence with 4 T2-prep durations of 13.62, 31.4, 80, and 110ms, and 6 diffusion-preps of b=400 and 800s/mm², 3 noncolinear directions. Reference scans took ~18min while Multitasking scan took ~9min. All protocols were scanned with resolution=1.5x1.5x5mm³, FOV=240x240mm², 20 slices/partitions with matched positions.

Results

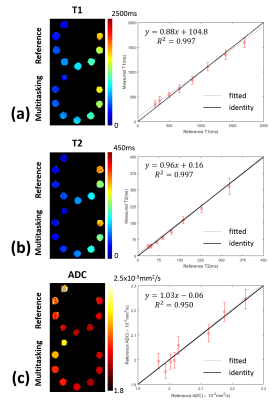
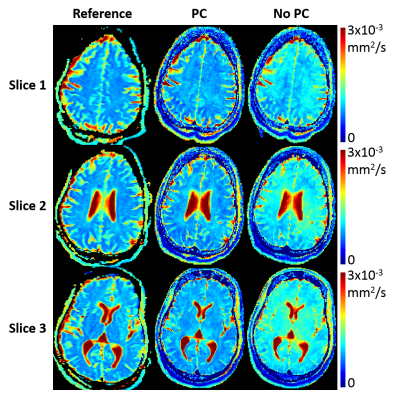
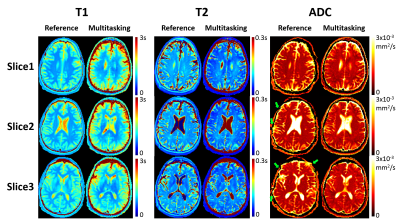
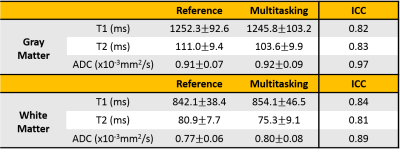
Phantom T1/T2/ADC mapping showed substantial quantitative agreement between Multitasking and references, with all

$R^{2}$ >0.95 (Fig. 2). In vivo study showed that the time-resolved phase correction provided more accurate ADC maps than without correction (Fig. 3). Representative brain T1/T2/ADC mapping of 3 slices using Multitasking demonstrated consistency with the references, providing co-registered maps without distortion (Fig. 4). Table 1 showed T1/T2/ADC measurements on 18 ROIs drawn on left and right frontal, parietal, and occipital regions of one upper, mid, and lower slice. The proposed method yielded intraclass correlation coefficients (ICC) of 0.82, 0.83, and 0.97 respectively on gray matter, and 0.84, 0.81, and 0.89 respectively on white matter against references.

Discussion

Simultaneous T1/T2/ADC mapping using Multitasking showed substantial quantitative consistency with reference scans. The time-resolved phase correction compensated for the phase inconsistency due to pulsatile motion, yielding more accurate ADC maps. All T1/T2/ADC measurements fell within the literature range^11,12.

Conclusion

We propose a novel 3D whole-brain simultaneous T1/T2/ADC mapping approach using Multitasking in ~9min, half of the time to collect separate reference measurements. The method has the added benefits of producing distortion-free (because of the use of gradient-echo readout instead of EPI readout), co-registered maps. Extending this work to leverage the established ability of the Multitasking framework to obtain motion-resolved quantitative mapping is a potential avenue to achieve simultaneous T1/T2/ADC mapping of the abdomen and heart.

Acknowledgements

This work was supported by NIH 1R01HL124649.

References

1. Langer DL, van der Kwast TH, Evans AJ, Trachtenberg J, Wilson BC, Haider MA. Prostate cancer detection with multi-parametric MRI: logistic regression analysis of quantitative T2, diffusion-weighted imaging, and dynamic contrast-enhanced MRI. J Magn Reson Imaging 2009;30(2):327-334.

2. Neema M, Stankiewicz J, Arora A, Dandamudi VS, Batt CE, Guss ZD, Al-Sabbagh A, Bakshi R. T1- and T2-based MRI measures of diffuse gray matter and white matter damage in patients with multiple sclerosis. J Neuroimaging 2007;17 Suppl 1:16S-21S.

3. Yankeelov TE, Lepage M, Chakravarthy A, Broome EE, Niermann KJ, Kelley MC, Meszoely I, Mayer IA, Herman CR, McManus K, Price RR, Gore JC. Integration of quantitative DCE-MRI and ADC mapping to monitor treatment response in human breast cancer: initial results. Magn Reson Imaging 2007;25(1):1-13.

4. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature 2013;495(7440):187-192.

5. Gras V, Farrher E, Grinberg F, Shah NJ. Diffusion-weighted DESS protocol optimization for simultaneous mapping of the mean diffusivity, proton density and relaxation times at 3 Tesla. Magn Reson Med 2017;78(1):130-141.

6. Zhang Y, Wells SA, Hernando D. Stimulated echo based mapping (STEM) of T1 , T2 , and apparent diffusion coefficient: validation and protocol optimization. Magn Reson Med 2018.

7. Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie YB, Wang N, Li DB. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nature Biomed Eng 2018;2(4):215-226.

8. Nguyen C, Fan Z, Xie Y, Pang J, Speier P, Bi X, Kobashigawa J, Li D. In vivo diffusion-tensor MRI of the human heart on a 3 tesla clinical scanner: An optimized second order (M2) motion compensated diffusion-preparation approach. Magn Reson Med 2016;76(5):1354-1363.

9. Gao Y, Han F, Zhou Z, Shao X, Zhong X, Wang DJ, Yang Y, Hu P. Diffusion-prepared multi-shot bSSFP imaging with gradient stablizer. In Proceedings of the 27th Annual Meeting of ISMRM, Paris, France, 2018.

10. Ma S, Nguyen C, Christodoulou A, Luthringer D, Kobashigawa J, Lee S-E, Chang H-J, Li D. Accelerated Cardiac Diffusion Tensor Imaging Using Joint Low-Rank and Sparsity Constraints. IEEE Trans BioMed Eng 2018;65(10): 2219-2230.

11. Bojorquez JZ, Bricq S, Acquitter C, Brunotte F, Walker PM, Lalande A. What are normal relaxation times of tissues at 3 T? Magn Reson Imaging 2017;35:69-80.

12. Wansapura JP, Holland SK, Dunn RS, Ball WS, Jr. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Imaging 1999;9(4):531-538.

Figures

Figure 1. (a) T1/T2/ADC Multitasking sequence diagram and corresponding signal evolution, and (b) k-space sampling demonstration. T2preps of various durations and diffusion-preps of various b-values and directions are placed in a row to generate T1-T2-diffusion weighting. One T2prep duration must match the diffusion-prep duration, serving as one b=0 shot. Crusher gradients are used to maintain consistent magnitude, yielding a T1-decay for Mxy and Mz decay component. Mz recovery component recovers towards thermal equilibrium with an 1s gap placed at the end of each shot. Imaging data are sampled with Gaussian density and training data are sampled every 8 readouts.

Figure 2. Simultaneous T1, T2, and ADC mapping of the phantom using Multitasking is compared against reference methods. Measured values agree with reference values with good correlation. Dotted lines represent the linear fitting between Multitasking and reference. Solid lines represent identity lines.

Figure 3. Comparison of in vivo brain ADC maps of 3 slices given by the reference, the Multitasking framework with the time-resolved phase correction (PC) and without the phase correction (No PC). The application of the time-resolved phase correction produces significantly more accurate ADC than without phase correction.

Figure 4. Representative in vivo brain T1, T2, and ADC maps of three slices using Multitasking are compared against reference methods. The proposed method provides consistent estimation with the reference. T1, T2, and ADC maps are co-registered without image distortion (green arrows).

Table 1. In vivo ROI measurements and intraclass correlation coefficients between Multitasking and the references on gray matter and white matter.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

0308