Synopsis

We developed a nonlinear model with simultaneous phase and magnitude updates for iterative multi-shot DWI reconstruction. In addition, locally low-rank regularization along the diffusion encoding direction was included in the proposed model to utilize angular correlation for DTI reconstruction. In-vivo high-resolution and high b-value images have been acquired to validate the proposed method and the proposed method significantly reduces image noise.

Introduction

Theory

Locally low-rank regularization for DTI

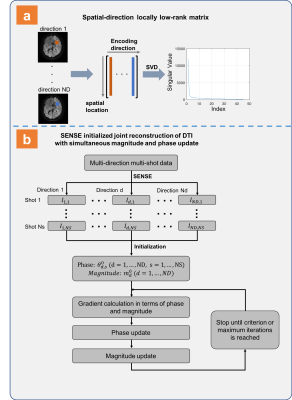
Typically, 30 or even more directions are acquired in DTI to achieve high SNR, which is far more than the minimum required 6 directions, thus some redundancy exists between different directions. Fig. 1a shows how we construct the spatial-direction locally low-rank matrix given the magnitude images of all directions.

Nonlinear model

To utilize the angular correlation, motion-induced phase variations between directions and shots need to be considered. The complex MR image can be written in terms of magnitude and phase explicitly, and then the k-space signal for direction d and shot s can be represented as the following,

$$ y_{d,s} = EFS(m_d \cdot e^{j\theta_{d,s}}) + n $$

where E, F and S represent sampling operator, Fourier transform and sensitivity encoding operator, respectively, $$$m_d$$$ represents the magnitude image after diffusion encoding along direction d, and $$$e^{j\theta_{d,s}}$$$ represents the phase of direction d, shot s, which may comes from B0 inhomogeneity, bulk motion and other sources, and n denotes noise.

We developed the following general model for joint DTI reconstruction,

$$\min_{m,\theta} \sum_{d = 1}^{ND}\sum_{s = 1 }^{NS}\frac{1}{2}\left \| E_{d,s}FS (m_{d} \cdot e^{j\theta_{d,s}}) - y_{d,s} \right \|_{2}^{2} + \lambda_{1}g_m(m) $$

where $$$ND$$$ is the number of diffusion encoding directions, and $$$NS$$$ is the number of shots. The first term in the cost function is about the forward model. The second term is a regularization term to utilize the correlation between images from different directions. In this work, we used LLR regularization as described aboe.

We use alternating minimization with respect to the magnitude and phase separately to solve the above problem^[7]. The phase of each shot and each direction can be updated independently, and the proximal gradient method is used to update magnitude. Fig. 1b shows the pipeline of the reconstruction using SENSE reconstruction as initialization^[8].

Methods

Experiment design and data acquisition

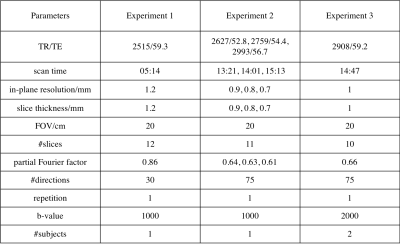
With IRB approval, data were acquired in four volunteers on a 3T GE Signa Premier scanner using a 2D DW EPI sequence and a 48-channel head coil. Three experiments were designed to demonstrate the feasibility of the proposed method (experiment 1), test the performance of the proposed method on high-resolution data (experiment 2), and high-b-value data (experiment 3), respectively. The scan parameters were shown in Table 1.

Image reconstruction and processing

Images were reconstructed with both the product MUSE^[9] and the proposed method (sensitivity maps from non-diffusion-weighted data using ESPIRiT^[10]). Diffusion data were processed using FSL's eddy function^[11]. DTI and BEDPOSTX models were fitted using FSL's dtifit and bedpostx functions.

Results and discussion

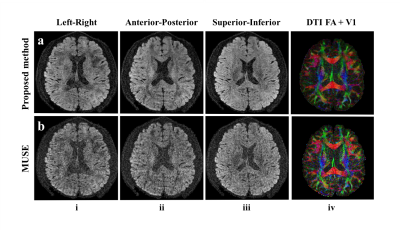
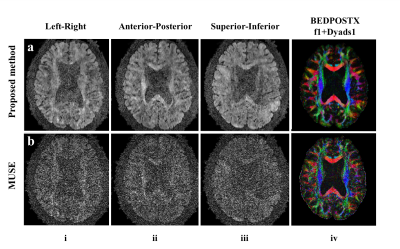
Figure 1 shows the results with 1.2mm isotropic resolution from product MUSE and the proposed method. The FA encoded V1 map from the proposed method is consistent with that from MUSE, which demonstrates the feasibility of the proposed method. The decreased noise level in the proposed method benefits from the fact all directions are reconstructed jointly, and a LLR regularization term is used to utilize their correlation.

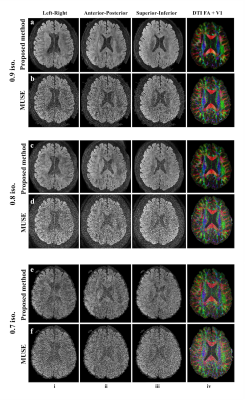
This improvement is more significant when the number of encoding directions and resolution are increased (Fig. 4). Figure 4 shows a representative slice reconstructed by these two methods under different resolutions. The DWIs reconstructed by MUSE (Fig. 4 rows b, d and f, columns i-iii) are very noisy, which results in unusable V1 maps (Fig. 4 rows b, d and f, column iv). While the proposed method shows markedly reduced noise level, and the reconstructed DWIs and V1 maps are clearly visually better (Fig. 4 rows a, c and e). The proposed method shows similar improvements for high b-value images as shown in Fig. 5 with resolution 1mm isotropic and b-value 2000.

Conclusion

Acknowledgements

Thank Frank Ong for sharing the code.

Research support from R01-EB009055, P41-EB015891 and GE Healthcare.

References

1. Le Bihan D, el al. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging2001;13:534–546.

2. Shi, Xinwei, et al. "Parallel imaging and compressed sensing combined framework for accelerating high‐resolution diffusion tensor imaging using inter‐image correlation." Magnetic resonance in medicine 73.5 (2015): 1775-1785.

3. Ma, Sen, et al. "Accelerated Cardiac Diffusion Tensor Imaging Using Joint Low-Rank and Sparsity Constraints." arXiv preprint arXiv:1801.03525 (2018).

4. Gao, Hao, et al. "PCLR: Phase‐constrained low‐rank model for compressive diffusion‐weighted MRI." Magnetic resonance in medicine 72.5 (2014): 1330-1341.

5. Veraart, Jelle, et al. "Denoising of diffusion MRI using random matrix theory." NeuroImage 142 (2016): 394-406.

6. Hu, Yuxin, et al. "Motion‐robust reconstruction of multishot diffusion‐weighted images without phase estimation through locally low‐rank regularization." Magnetic resonance in medicine (2018).

7. Ong, Frank, Joseph Y. Cheng, and Michael Lustig. "General phase regularized reconstruction using phase cycling." Magnetic resonance in medicine 80.1 (2018): 112-125.

8. Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic resonance in medicine 42.5 (1999): 952-962.

9. Chen, Nan-kuei, et al. "A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE)." Neuroimage 72 (2013): 41-47.

10. Uecker, Martin, et al. "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA." Magnetic resonance in medicine 71.3 (2014): 990-1001.

11. Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. Fsl. Neuroimage 2012;62:782– 790. doi: 10.1016/j.neuroimage.2011.09.015.