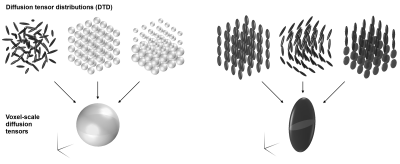
Macro- vs. Micro-Anisotropy
1Clinical Sciences, Lund, Lund University, Lund, Sweden, 2Laboratory for Mathematics in Imaging, Harvard Medical School, Boston, MA, United States
Synopsis
What are the distinguishing marks of anisotropic structures in a microscope, and how are these features reflected in the diffusion weighted signal? The lecture will survey the features of anisotropic diffusion on the micro- and macro-scale and connect them to the MRI experiments that may be used to probe such features.
Lecture overview
Diffusion is anisotropic when it depends on object rotation, i.e., the diffusion characteristics are not the same along all directions. Anisotropy can be captured by various representations or models1 based on the diffusion weighted signal along multiple encoding directions. However, anisotropy may be present even if the signal on the voxel scale is rotationally invariant! Imagine, for example, tissue that comprises randomly oriented cylinders; these are anisotropic on the microscopic scale but appear isotropic on the voxel scale. Anisotropy can therefore be considered on both microscopic and macroscopic scales2,3—from the level of coherent cell structures to whatever remains to the scale of the voxel.
At first glance, it may seem impossible to recover anisotropy from signal that is identical in all directions. Nevertheless, several techniques have been developed to disentangle microscopic anisotropy from orientation dispersion based on non-conventional diffusion encoding2,4-10. These methods include, for example, double/multiple diffusion encoding2,3 and q-trajectory encoding10, which constitute a set of probes that are sensitive to features beyond those accessible by the canonical Stejskal-Tanner experiment11.
The lecture will survey the features of anisotropy on the micro- and macro-scale, and show how these are revealed when non-conventional encoding is brought to bear.
Acknowledgements
No acknowledgement found.References
1 Novikov, D. S., Kiselev, V. G. & Jespersen, S. N. On modeling. Magn. Reson. Med., doi:10.1002/mrm.27101 (2018).
2 Cory, D. G., Garroway, A. N. & Miller, J. B. Applications of Spin Transport as a Probe of Local Geometry. Abstr Pap Am Chem S 199, 105 (1990).
3 Mitra, P. Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement. Physical Review B 51, 15074-15078, doi:10.1103/PhysRevB.51.15074 (1995). 4 Avram, A. V., Ozarslan, E., Sarlls, J. E. & Basser, P. J. In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient (qPFG) diffusion MRI on a clinical scanner. Neuroimage 64, 229-239, doi:10.1016/j.neuroimage.2012.08.048 (2013).
5 Komlosh, M. E. et al. Detection of microscopic anisotropy in gray matter and in a novel tissue phantom using double Pulsed Gradient Spin Echo MR. J. Magn. Reson. 189, 38-45, doi:10.1016/j.jmr.2007.07.003 (2007).
6 Özarslan, E. & Basser, P. J. Microscopic anisotropy revealed by NMR double pulsed field gradient experiments with arbitrary timing parameters. J. Chem. Phys. 128, 154511, doi:10.1063/1.2905765 (2008).
7 Lawrenz, M. & Finsterbusch, J. Detection of microscopic diffusion anisotropy on a whole-body MR system with double wave vector imaging. Magn. Reson. Med. 66, 1405-1415, doi:10.1002/mrm.22934 (2011).
8 Lasič, S., Szczepankiewicz, F., Eriksson, S., Nilsson, M. & Topgaard, D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics 2, 11, doi:10.3389/fphy.2014.00011 (2014).
9 Eriksson, S., Lasič, S., Nilsson, M., Westin, C. F. & Topgaard, D. NMR diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J. Chem. Phys. 142, 104201, doi:10.1063/1.4913502 (2015).
10 Westin, C. F. et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 135, 345-362, doi:10.1016/j.neuroimage.2016.02.039 (2016).
11 Stejskal, E. O. & Tanner, J. E. Spin Diffusion Measurement: Spin echoes in the Presence of a Time-Dependent Field Gradient. the journal of chemical physics 42, 288-292 (1965).
12 Basser, P. J., Mattiello, J. & Le Bihan, D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 66, 259-267, doi:10.1016/S0006-3495(94)80775-1 (1994).
13 Szczepankiewicz, F. Imaging diffusional variance by MRI: The role of tensor-valued diffusion encoding and tissue heterogeneity Ph.D. Thesis thesis, Lund University, (2016).
Figures