Reduced FOV, Reference Scans, Gradient Pre-Emphasis
1Center for MR Research and Department of Radiology, University of Illinois at Chicago, Chicago, IL, United States
Synopsis
This lecture focuses on three pulse sequence strategies to improve the image quality. First, methods for reducing the field-of-view (FOV) are described using examples of spatial saturation, multiple one-dimensional selective RF pulses, and/or multi-dimensional RF excitation. Second, reference scans are presented for measuring errors in k-space and enabling various phase corrections in pulse sequences utilizing echo trains. Third, gradient pre-emphasis is discussed as an effective method to reduce the adverse effects caused by eddy currents. Although these three topics may appear isolated, together they reflect a central theme of how to improve image quality by managing the artifacts.
Target Audience
This lecture is designed for scientists and clinicians who are interested in understanding three advanced features in image acquisition, namely, reduced field-of-view (FOV), reference scans, and eddy current reduction using gradient pre-emphasis.Objectives
To understand (a) common methods for reducing the FOV without suffering from aliasing artifacts, (b) strategies for estimating errors in k-space using reference scans, and (c) management of eddy currents using gradient pre-emphasis.Introduction
Increasing the spatial resolution and reducing the scan times are the two primary goals for MRI. Advanced pulse sequences have played a pivotal role in both areas. However, they also brought about a number of physics and engineering challenges, resulting in compromised image quality. This lecture focuses on three specific examples to illustrate how these challenges can be met. First, pulse sequence strategies for reducing the field-of-view (FOV) are described to allow high spatial resolution without suffering from spatial aliasing. Second, reference scans for measuring errors in k-space are presented and their performance in reducing artifacts is demonstrated. Lastly, gradient pre-emphasis is discussed. Although these three topics may appear isolated, together they reflect a central theme of how to improve image quality by managing the artifacts.Imaging with Reduced FOV
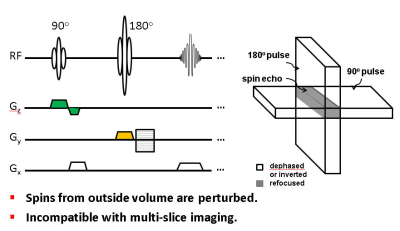
It is well known that signals outside the FOV can alias, producing characteristic artifacts depending on the specific k-space sampling strategy1. To avoid aliasing artifacts, the FOV is typically chosen to include the entire spatial extent of a subject, leading to a limited spatial resolution. Several techniques, however, have been developed to restrict the FOV to a fraction of a regular FOV without being subject to aliasing. This allows high spatial resolution to be achieved over a zoomed region. A straight-forward solution is to employ radiofrequency (RF) saturation pulses to eliminate the signals away from the targeted region1,2. Alternatively, multiple RF pulses can be used with their spatial selection gradients along different directions. For example, a combination of 90° and 180° RF pulses with non-parallel slice-selection gradients can select a slice with a reduced FOV (Fig. 1)3–5. Obviously, these sequence designs interrupt the spins away from the selected regions, compromising multi-slice imaging capability. This problem can be effectively addressed using 2D RF excitation1,6, together with slice tilting7–12. The principals involved in the 2D RF pulse design will be described and practical implementations presented.Reference Scans
Reference scans are typically performed prior to the actual scan for measuring errors in k-space. The measured errors are corrected in the subsequent image acquisition and/or reconstruction. Although phase errors are of primary interest, imperfections in signal amplitude can also be measured using reference scans13. A common source of phase errors is eddy currents which are particularly detrimental in echo-train pulse sequences that rely on coherence of transverse magnetization. Even on an MRI system with well compensated eddy currents, reference scans are often necessary to measure errors caused by a minute amount of residual eddy currents that can result in non-negligible artifacts1.
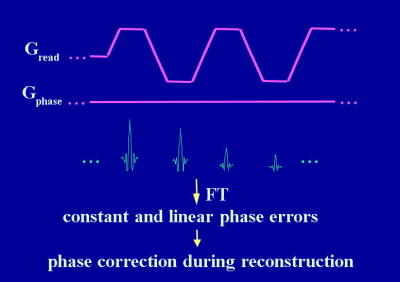
Reference scans can be acquired by disabling the phase-encoding gradient in an echo-train pulse sequence (Fig. 2)14,15. The underlying assumption is that the phase of each echo would be identical in the absence of inconsistent phase errors. Any deviation from this ideal situation can be measured by comparing the phases among the echo signals. Although the phase difference can be decomposed into multiple spatial dependencies, the vast majority of reference scans focus on only two phase components: (a) a spatially constant component or zeroth-order phase, and (b) a spatially linear component or first-order phase. In fast imaging pulse sequences, these two components are responsible for the majority of the artifacts.
Reference scans can alternatively be acquired without disabling the phase-encoding gradient. Examples of these strategies include PLACE16, phase-encoded reference scan17, and two-frame phase labeling18. k-Space errors can also be estimated without acquiring a reference scan at all19–21.
Gradient Pre-emphasis
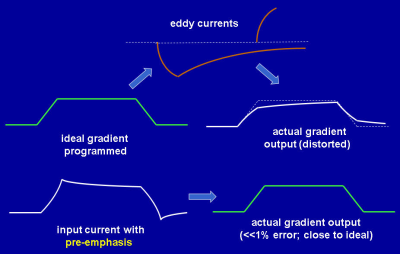
While effects caused by a small amount of residual eddy currents can be corrected for using reference scans, more substantial eddy currents are commonly compensated by gradient coil shielding and waveform pre-emphasis. The idea behind gradient waveform pre-emphasis is to intentionally distort the current waveform delivered to the gradient coil, such that the pre-emphasis distortion cancels the predicted eddy current distortion (Fig. 3). The effectiveness of waveform pre-emphasis depends strongly on the accuracy of eddy current measurements. With an accurate eddy current measurement, gradient pre-emphasis can reduce eddy current levels by one to two orders of magnitude.
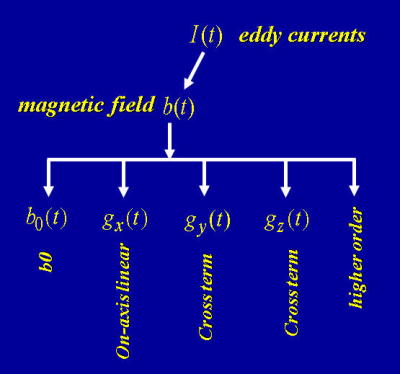
Characterization of eddy currents requires a quantitative model to describe their spatiotemporal features. The spatial dependence is best described using a spherical harmonic decomposition or a Taylor series expansion (Fig. 4). The spatially independent term is often called the “B0 eddy currents”, while the spatially linear terms are referred to as the “linear eddy currents”. The B0 eddy currents can be compensated by using a separate B0 coil or by modifying the receiver frequency or phase. The linear eddy currents are most effectively addressed by gradient waveform pre-emphasis.
The temporal dependence of eddy currents is typically analyzed using a linear model, such as the one proposed by Jehenson et al22. This model uses a series of amplitudes and time constants to describe eddy currents with any spatial dependence. It is important to recognize that the sensitivity of different pulse sequences to time constant is drastically different. For example, single-shot echo planar imaging (EPI) is most sensitive to eddy currents with short time constants (e.g., 400-800 μs), whereas diffusion-weighted EPI pulse sequences with a Stejskal-Tanner gradient pair are sensitive to much longer time constants (e.g., 30-100 ms). For a given eddy current amplitude, the time constant that produces the worst adverse effect is referred to as critical time constant23. Several pulse sequences for characterizing eddy currents over a broad range of time constants (e.g., 10 µs – 2 s) will be described.
Acknowledgements
The author thanks Drs. Yi Sui, Jiaxuan Zhang, Novena Rangwala, Girish Srinivasan, Muge Karaman, Kevin King, Yiping Du, and Zheng Zhong for their help.References
1. Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. San Diego, California: Elsevier Academic Press; 2004.
2. Le Roux P, Gilles RJ, McKinnon GC, Carlier PG. Optimized outer volume suppression for single-shot fast spin-echo cardiac imaging. J Magn Reson Imaging. 8(5):1022-1032.
3. Symms MR, Wheeler-Kingshot CA, Parke GJM, Barker GJ. Zonally-magnified oblique multislice (ZOOM) EPI. In: Proceedings of the ISMRM Eighth Meeting. Denver, Colorado; 2000:160.
4. Rangwala N, Zhou XJ. Reduction of fast spin echo cusp artifact using a slice-tilting gradient. Magn Reson Med. 2010;64(1):220-228.
5. Jeong E-K, Kim S-E, Guo J, Kholmovski EG, Parker DL. High-Resolution DTI with 2D Interleaved Multislice Reduced FOV Single-Shot Diffusion-Weighted EPI (2D ss-rFOV-DWEPI). Magn Reson Med. 2005;54:1575-1579.
6. Saritas EU, Cunningham CH, Lee JH, Han ET, Nishimura DG. DWI of the spinal cord with reduced FOV single-shot EPI. Magn Reson Med. 2008;60(2):468-473.
7. Finsterbusch J. Fast-spin-echo imaging of inner fields-of-view with 2D-selective RF excitations. J Magn Reson Imaging. 2010;31(6):1530-1537.
8. Finsterbusch J. Improving the performance of diffusion-weighted inner field-of-view echo-planar imaging based on 2D-Selective radiofrequency excitations by tilting the excitation plane. J Magn Reson Imaging. 2012;35(4):984-992.
9. Banerjee S, Saritas EU, Melkus, G Shankaranarayanan J. Tilted 2D RF Excitation with Extended Slice Coverage for High-Resolution Reduced-FOV DWI. In: 21st Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM); 2013:57.
10. Sui Y, Damen FC, Xie K, Zhou XJ. Image Domain Segmented Diffusion Imaging Using A 2D Excitation RF Pulse for Distortion Reduction. In: Proceedings of the 22nd Annual Meeting of the ISMRM. Milan, Italy; 2014:608.
11. Zhou XJ, Sui Y. Image domain segmented echo planar magnetic resonance imaging using a 2D excitation radiofrequency pulse. US Patent No 9,797,970. October, 2017.
12. Taviani V, Alley MT, Banerjee S, et al. High-resolution diffusion-weighted imaging of the breast with multiband 2D radiofrequency pulses and a generalized parallel imaging reconstruction. Magn Reson Med. 2017;77(1):209-220.
13. Zhou XJ, Liang ZP, Cofer GP, Beaulieu CF, Suddarth SA, Johnson GA. Reduction of ringing and blurring artifacts in fast spin-echo imaging. J Magn Reson Imaging. 1993;3(5):803-807.
14. Zhou XJ, Cofer GP, Hinks RS, MacFall JR, Johnson GA. On Phase Artifacts in Fast Spin-Echo Images. In: Abstract of the 12th Annual Meeting of the Society of Magnetic Resonance in Medicine. New York, NY; 1993:1248.
15. Hinks SR, Kohli J, Washburn S. Fast Spin Echo Prescan for Artifacts Reduction. In: Proceedings of Annual Meeting of the SMR. Nice, France; 1995:634.
16. Xiang Q-S, Ye FQ. Correction for geometric distortion and N/2 ghosting in EPI by phase labeling for additional coordinate encoding (PLACE). Magn Reson Med. 2007;57(4):731-741.
17. Hu X, Le T. Artifact reduction in EPI with phase‐encoded reference scan. Magn Reson Med. 1996; 36:166-171.
18. Xie VB, Lyu M, Wu EX. EPI Nyquist ghost and geometric distortion correction by two-frame phase labeling. Magn Reson Med. 2017;77(5):1749-1761.
19. Buonocore M, Gao L. Ghost artifact reduction for echo planar imaging using image phase correction. Magn Reson Med. 1997; 38:89-100.
20. Lee J, Jin KH, Ye JC. Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA). Magn Reson Med. 2016;76(6):1775-1789.
21. Chen Y, Liao Y, Yuan L, et al. Referenceless one-dimensional Nyquist ghost correction in multicoil single-shot spatiotemporally encoded MRI. Magn Reson Imaging. 2017; 37:222-233.
22. Jehenson P, Westphal M, Schuff N. Analytical method for the compensation of eddy-current effects induced by pulsed magnetic field gradients in NMR systems. J Magn Reson. 1990;90(2):264-278.
23. Zhou XJ. Quantitative Analysis of Eddy Current Effects on Echo Planar Images. In: Proc. 4th ISMRM; 1996:1486.
Figures