Target audience

Scientists interested in the basic physics of diffusion in biological tissue

Outcome/objectives

To gain a fundamental understanding of the physics of particles diffusing in complex media, supporting the ability of the participants to interpret and critically appraise diffusion MRI measurements.

Methods

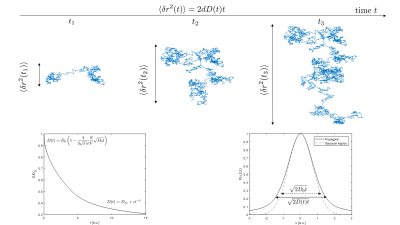
Diffusion is the random motion of molecules, a kinetic manifestation of the thermal energy at any non-vanishing temperature. A basic understanding of its properties can be obtained by the picture of a ”random walk”, from which e.g. the relation $$$\left\langle \delta {{r}^{2}} \right\rangle =2dDt$$$ for the mean square displacement $$$\left\langle \delta {{r}^{2}} \right\rangle $$$ of molecules (in $$$d$$$ dimensions) during the time interval $$$t$$$ can be derived (1-3). The diffusion coefficient, $$$D$$$ in the equation, is a fundamental property of the medium, and is about 3 $$$\mu$$$m­2/ms for pure water at 37°C. This means that during e.g. 50 ms, a diffusion time relevant for MRI, molecules sample distances on the order of 10 $$$\mu$$$m of their environment, roughly the scale of individual cells. This property underlies the potential of diffusion to be used as a sensitive probe tissue microstructure (4,5). The random walk is also the conceptual basis of Monte Carlo simulations of diffusion. A central quantity for understanding diffusion, is the so-called propagator $$$P(r,{{r}_{0}};t)$$$, whose magnitude gives the probability for a molecule initially at $$${{r}_{0}}$$$ to be found at $$$r$$$ after a time $$$t$$$ (3,6). As such, the propagator embodies the basic statistics of the diffusion process, and can be used to compute the MRI signal (7). Finding the diffusion propagator usually entails following the diffusion equation (also known as Fick’s 2nd law) (6) $$\frac{d}{dt}P(r,{{r}_{0}};t)=\nabla \cdot \text{D}\nabla P(r,{{r}_{0}};t)$$ which follows from the basic principle of mass conservation as well as Ficks first law, relating particle current to probability gradients. In this equation, we generalized from the diffusion constant $$$D$$$ to the 2nd rank diffusion tensor D, allowing for diffusion anisotropy. The solutions to the diffusion equation depend critically on boundary conditions, i.e. specification of the propagator or the current at e.g. tissue boundaries and interfaces. This is how the structure of the medium enters the formalism, and plays a crucial role in the appearance of the propagator (6,8). The most simple case of free diffusion, corresponding to a vanishing propagator at infinite distances, corresponds to the fundamental Gaussian expression (in $$$d=1$$$, $$$r\to x$$$) $$P(x,x_0;t)=\frac{1}{\sqrt{4\pi Dt}}{{e}^{-{{(x-{{x}_{0}})}^{2}}/(4Dt)}}$$ This solution is a component of many biophysical models of diffusion in tissue (9-12), specifically multiple gaussian compartments models, which can report on compartment volume fractions and diffusivities (4,13,14). The diffusion equation can be solved exactly only for a handful of other cases, such as diffusion between parallel plates, or inside spheres or cylinders, and these solutions also appear in biophysical diffusion models. Alternatively, the diffusion equation can be solved numerically using methods for partial differential equations such as finite elements. In general, the solution is not a Gaussian, although it can remain an arbitrarily good approximation on certain spatiotemporal scales. This explains the usefulness of the cumulant expansion (underlying e.g. diffusion kurtosis imaging) (5,15-18), which is essentially an expansion around a Gaussian distribution, each term accounting for finer and finer deviations from Gaussianity. Technically, the cumulant expansion is an expansion of the so-called characteristic function(15), the Fourier transform of the propagator, which is closely related to the MR diffusion signal(7). A full solution for the propagator in complex media such as biological tissue is not possible in general. A number of results exists for e.g. the time-dependent diffusivity nevertheless. For example, at short diffusion times, the so-called Mitra limit (19) applies $$D(t)={{D}_{0}}\left( 1-\frac{4}{3\sqrt{\pi }\,d}\frac{S}{V}\sqrt{{{D}_{0}}t}+\mathcal{O}(t) \right)$$ where $$$D_0$$$ is the microscopic diffusivity ($$$D(t\to 0$$$)) facilitating in principle a measurement of S/V, the surface to volume ratio of reflecting interfaces. In the opposite limit of long diffusion times $$D(t)\sim{\ }{{D}_{\infty }}+c{{t}^{-\tilde{\upsilon} }}$$ where $$$\tilde{\upsilon}$$$ is an exponent determined by the characteristics (correlation) of obstacles to the diffusing particles (20,21). In the tortuosity limit $$$t=\infty$$$, $$$D=D_\infty=D_0/\lambda^2$$$, where the tortuosity $$$\lambda$$$ reflects how much obstacles on average increase the distance of the shortest path between any two points. This equation implies a finite $$$D_\infty$$$, in agreement with measurements of diffusion in tissue. Note that this contradicts so-called anomalous diffusion and stretched exponentials, which imply that $$$D_\infty = 0$$$ or $$$D_\infty = \infty$$$ (even $$$D(t) = \infty$$$ for all $$$t$$$, for the latter case) (14). The finite $$$D_\infty$$$ is a consequence of the central limit theorem, which gives very broad conditions for the approach of sums of random variables (the random walk) to a Gaussian distribution (1). The time-dependent diffusivity can equivalently be studied in terms of frequency dependency of the velocity autocorrelation function, the Fourier transform of $$$\mathcal{D}(t)\equiv \theta (t)\left\langle v({{t}_{0}})v(t+{{t}_{0}}) \right\rangle $$$ (22,23).

Acknowledgements

The author acknowledges support from the Dagmar Marshall foundation.

References

1. Bouchaud JP, Georges A. Anomalous Diffusion in Disordered Media - Statistical Mechanisms, Models and Physical Applications. Phys Rep 1990;195(4-5):127-293. 2. Haus JW, Kehr KW. Diffusion in Regular and Disordered Lattices. Phys Rep 1987;150(5-6):263-406. 3. Chaikin PM, Lubensky TC. Principles of condensed matter physics. Cambridge: Cambridge University Press; 1995. 4. Novikov DS, Jespersen SN, Kiselev VG, Fieremans E. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. ArXiv e-prints. Volume arXiv:1612.02059 [physics.bio-ph]2016. 5. Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed 2017;30(3):e3602-n/a. 6. Crank J. The mathematics of diffusion. Oxford, Eng: Clarendon Press; 1975. viii, 414 p. p. 7. Callaghan PT. Translational dynamics and magnetic resonance : principles of pulsed gradient spin echo NMR. Oxford ; New York: Oxford University Press; 2011. xvii, 547 p. p. 8. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Mod Phys 2007;79(3):1077-1137. 9. Jespersen SN, Bjarkam CR, Nielsen T, Hansen B, Vestergaard-Poulsen P. Dendrite density from magnetic resonance diffusion measurements: comparison with histology. 2007; Berlin, Germany. 10. Kroenke CD, Ackerman JJ, Yablonskiy DA. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn Reson Med 2004;52(5):1052-1059. 11. Yablonskiy DA, Sukstanskii AL. Theoretical models of the diffusion weighted MR signal. NMR Biomed 2010;23(7):661-681. 12. Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage 2011;58(1):177-188. 13. Nilsson M, van Westen D, Stahlberg F, Sundgren PC, Latt J. The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. Magma 2013;26(4):345-370. 14. Novikov DS, Kiselev VG, Jespersen SN. On modeling. Magn Reson Med 2018;79(6):3172-3193. 15. Kampen NGv. Stochastic processes in physics and chemistry. Amsterdam ; Boston: Elsevier; 2007. xvi, 463 p. p. 16. Risken H. The Fokker-Planck equation: methods of solution and applications. Berlin: Springer-Verlag; 1984. 17. Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed 2010;23(7):698-710. 18. Jensen JH, Helpern JA, Ramani A, Lu HZ, Kaczynski K. Diffusional kurtosis imaging: The quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine 2005;53(6):1432-1440. 19. Mitra PP, Sen PN, Schwartz LM, Le Doussal P. Diffusion propagator as a probe of the structure of porous media. Phys Rev Lett 1992;68(24):3555-3558. 20. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences 2014. 21. Novikov DS, Kiselev VG. Effective medium theory of a diffusion-weighted signal. NMR Biomed 2010;23(7):682-697. 22. Novikov DS, Kiselev VG. Surface-to-volume ratio with oscillating gradients. J Magn Reson 2011;210(1):141-145. 23. Does MD, Parsons EC, Gore JC. Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magn Reson Med 2003;49(2):206-215.