MRI: The Classical Description
1National Institutes of Health, United States
Synopsis
This lecture will cover the basics of MRI physics and image formation using the classical description. It will describe the basic concepts in magnetic moments, net magnetization of tissue and precession, as well as the manipulation of magnetization using RF pulses and magnetic field gradients to generate an image. Spin echoes and gradient echoes will be described along with the basics of T1 and T2 relaxation and their effect on image contrast. The Bloch equations will be used to summarize the evolution of magnetization and pulse sequence diagrams will be introduced to describe image formation.
Target Audience
Physicists and engineers who wish to deepen their understanding of MRI physics and pulse sequences.Objectives
Following this lecture, audience members should be able to:
- Describe basic concepts in MRI theory including magnetic moments, net magnetization and precession
- Understand how RF pulses, magnetic field gradients and signal echoes are used to generate an MR image
- Describe relaxation and the effect on image contrast
- Understand how the Bloch equations are used to calculate the evolution of magnetization
Net Magnetization
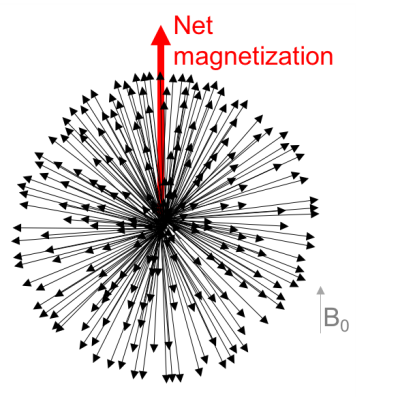
A full explanation of MRI physics requires a quantum mechanical approach, but many of the principles can be adequately explained with classical descriptions since we are dealing with the collective behavior of an ensemble of nuclei. In order to understand the classical description, we must know that the atomic nucleus of hydrogen (1H, a proton) produces a small magnetic field, a “magnetic moment”, as it rotates. This nuclear property is called “spin”. When placed in an external magnetic field (B0), the nuclei tend to realign to be parallel or anti-parallel to the magnetic field, with an excess of only a few per million oriented parallel to the field, magnetizing the entire hydrogen-containing sample (Figure 1). In addition to hydrogen, this same principle is true for other elements (eg. 31P, 23Na, 13C). Readers are directed to the many excellent text books on MRI physics for more detailed descriptions [1-2].
At equilibrium, the nuclei precess around an external field, in a process similar to the wobbling of a spinning top, with angular frequency proportional to the gyromagnetic ratio ($$$\gamma$$$), constant for each nucleus) and the magnetic field strength (B) as given by the Larmor frequency ($$$\omega$$$):
$$\omega=\gamma B $$
The ensemble of protons precess incoherently, and they are continuously interacting with their own local chemical environments as they bounce around and diffuse through the sample.
RF pulses
In order to observe the tissue magnetization vector, we tip it away from its alignment with the main magnetic field (z-axis) into the “transverse plane” (xy-plane) using a B1(t) field. A B1(t) field is much weaker than a B0 field, but it is oscillating at the Larmor frequency, and therefore can push the magnetization because of its synchrony with the natural oscillation frequency of the net magnetization. We can think of the spins precessing around both the static B0 and rotating B1(t), skewing the distribution of the population toward the B1(t) field and generating some phase coherence which manifests as an observable magnetization vector in the transverse plane.
It is often easier to think of the motion of the bulk magnetization in a reference frame rotating at the Larmor frequency. The angle of rotation (the tip angle) is modified by the power or duration of the RF pulse.
Signal reception
Following the RF pulse, there is an oscillating signal in the transverse plane as the magnetization vector rotates around at the Larmor frequency which generates a current in the receiver coils that can be detected and used as an MRI signal.
T1, T2 and T2* relaxation
T1 and T2 relaxation are two distinct processes that occur at the same time as the magnetization returns to equilibrium. T1 relaxation returns the longitudinal magnetization (Mz) to alignment with the main magnetic field as the spins return to their equilibrium distribution:
$$M_z (t)= M_0 (1-e^{-t/T_1})$$
T2 relaxation is the decay of the transversal components of the magnetization (Mxy) caused by the loss of phase coherence of the populations of spins:
$$M_{xy} (t)= M_0 e^{-t/T_2}$$
These two processes occur on very different time scales, with T2 relaxation occurring very rapidly compared to T1 relaxation.
T2* relaxation describes the accelerated decay of the Mxy from local magnetic field inhomogeneities that cause spins to lose their coherence more quickly.
MR images use the inherent tissue differences in T1 and T2 to generate contrast.
Spatial Encoding
In order to generate spatial information from the NMR signal, we use magnetic field gradients (Gx, Gy and Gz). In other words, we vary the strength of the magnetic field along each dimension in the MRI scanner such that
$$B =B_0+G_x x+G_y y+G_z z$$
When the field varies in space, so does the resonant frequency (from the Larmor equation), which allows us to spatially encode our signal.
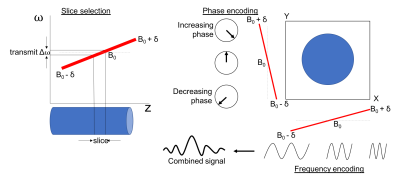
Slice selection is achieved with a linear variation of resonant frequencies along the slice-encoding direction at the same time that the RF pulse is applied. The frequency of the RF pulse corresponds to a chosen slice location and the transmit bandwidth of the RF pulse, or the small range of frequencies used for the RF pulse, excites a slab of tissue of a given thickness.
Frequency encoding is applied during signal acquisition, such that the tissues at different spatial locations contribute different frequencies to the signal. Phase encoding gradients are applied prior to signal acquisition in the direction perpendicular to frequency encoding. This produces a linear difference in phase prior to signal acquisitions. Phase encoding is repeated a number of times with different gradient amplitudes such that each data acquisition has a different spatially dependent phase (Figure 2).
The MRI signal is composed of many frequencies from all tissue within the slice and a Fourier Transform is used to convert the encoded data into an image.
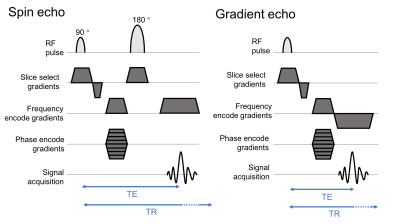
Pulse sequence diagrams (Figure 3) are used to summarize RF pulse and gradient event used to make an image.
Echoes
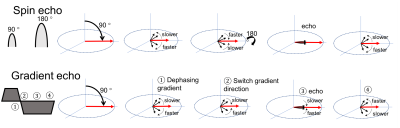
Two common types of echoes used during imaging are gradient echoes and spin echoes (Figure 4). A spin echo is uses a 180° pulse to reverse the relaxation cause by magnetic field inhomogeneity causing a rephasing of the signal (echo) weighted by T2 relaxation. Gradient echoes are controlled by the application of magnetic field gradients. When the gradients are switched on, the protons quickly lose phase coherence and, when reversed, the signal reappears and produces a signal echoes weighed by T2* relaxation.Bloch Equations
The Bloch equations [4] provide a complete classical description of the evolution of the magnetization during an MRI experiment.
Precession:
$$ ∂M/∂t= γM×B$$
Expanded:
$$∂M_x/∂t=γ(M_y B_z- M_z B_y )-M_x/T_2 $$
$$∂M_y/∂t= γ(M_z B_x- M_x B_z )-M_y/T_2 $$
$$∂M_z/∂t= γ(M_x B_y- M_y B_x )-(M_z-M_0)/T_1 $$
Acknowledgements
Many thanks to all who have covered this material in the pastReferences
[1] Haacke EM, Brown RW, Thompson MR, Venkatesan R, Magnetic Resonance Imaging: Physical Principles and Sequence Design, Wiley-Liss (1999)
[2] Liang Z and Lauterner PC, Principles of Magnetic Resonance Imaging: A signal processing perspective, IEEE Press (2000)
[3] Bernstein MA, King KF and Zhou XJ, Handbook of MRI Pulse Sequences, Elsevier (2004)
[4] Bloch F, Nuclear Induction, Phys. Rev. 70, 460 (1946)
Figures