Synopsis

Magnetisation transfer (MT) has been found to contribute to parameter estimation bias in sequences used in the two-pool relaxometry technique, mcDESPOT. Recent work shows that using controlled saturation magnetisation transfer (CSMT) RF-pulses, a two-pool system (free- and bound-pools) can behave as a single pool with modified equilibrium magnetisation and longitudinal relaxation rate. Here, we investigate the use of CSMT to model MT-effects in a three-pool system (exchange + MT) and show that under these conditions, signal behaves as a two-pool system and matches a mcDESPOT model but characterised by different parameters than those originally assumed.

Introduction

Multicomponent DESPOT (mcDESPOT) models tissue response using a system of two or more exchanging ‘free’ (i.e. MR-visible) magnetisation components.¹ In its two-pool form, mcDESPOT has been used for characterisation of white matter (WM), with the two components usually identified as intra/extracellular water (slow-relaxing) and myelin-water (fast-relaxing). The myelin water fraction (MWF) calculated from these estimates has been shown to consistently overestimate the value derived from multiecho CPMG methods.^2,3 WM is known to yield a strong magnetisation transfer (MT) effect that is not ordinarily modelled in mcDESPOT; other work has suggested this to be a source for MWF overestimation.^4,5

The MT-effect may be modelled by the addition of a ‘bound’ (i.e. macromolecular) pool of magnetisation.^5,6 RF-pulses rotate ‘free’ magnetisation, but saturate ‘bound’ magnetisation according to applied RF-power $W$ (Equation 1), where $B_{1,rms}$ is RMS pulse amplitude over the whole sequence and $G$ is bound-pool absorption factor.

$$W=\pi G(\Delta)\gamma^2B_{1,rms}^2$$

The recently proposed controlled saturation magnetisation transfer (CSMT) approach has been shown to allow a simple two-pool MT-system (i.e. one free-pool, one bound-pool) to behave as a single free-pool during DESPOT-style relaxometry by keeping $W$ constant over all acquisitions, irrespective of the applied flip angle (FA).⁷

In this work, we aim to extend this approach to consider a system with two free components, of the type typically modelled in mcDESPOT. We consider how a ‘ground-truth’ scenario with three pools (i.e. two free-pools and one bound-pool) will produce parameter estimation bias when fitted using a two-pool model that does not include any bound component (hereafter referred to as the ‘mcDESPOT’ model).

Methods

Figure 1 illustrates our three-pool configuration, including a bound-pool to account for MT-effects.⁵ We use the Bloch-McConnell equations to model the evolution of magnetisation for such a system and calculate steady-state solutions independently for SPGR and bSSFP. We then fit a mcDESPOT model to three-pool (ground-truth) signals, simulated using either controlled (i.e. same $W$ regardless of FA) or uncontrolled saturation methods. Least-square criteria, using fmincon in Matlab2016b, were applied.

Comparison of the differential equations governing mcDESPOT and three-pool models suggests that the latter can be fitted using a mcDESPOT model, with 'apparent' parameters shown in Figure 2. Note that the assumption made in this derivation is that the bound-pool is in a steady-state.

Results and Discussion

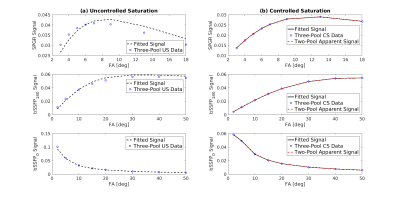
When saturation is uncontrolled, a mcDESPOT model fits poorly (NRMSE = 6.4%) to simulated three-pool data, particularly for SPGR (Figure 3a). This results in inaccurate parameter estimation due to the dependence of each apparent parameter on RF-power. In contrast, the same model fits very well (NRMSE = 0.03%) for simulated controlled saturation data (Figure 3b). The signal predicted using the mcDESPOT model with the apparent parameter values in Figure 2 also fits very well (NRMSE = 0.25%), although not perfectly because the bound-pool steady-state assumption is an approximation. Using CSMT, a three-pool system behaves as a two-pool model, characterised by the parameters in Figure 2; model dimensionality is reduced without explicit modelling of a bound-pool, as has been performed previously.⁵

Figure 2 indicates that given no direct exchange between MR-visible pools, an apparent exchange ($\Delta k_{FS}$) remains that is solely mediated by the bound-pool; these additional exchange pathways are highlighted in Figure 1. This implies that the exchange rates observed using mcDESPOT could reflect exchange mediated purely by MT. $\Delta k_{FS}$ increases almost linearly with $k_{B}$ but decreases for larger $B_{1,rms}$, as magnetisation entering the bound-pool is lost through saturation.

Figures 4 and 5 use the derived parameter expressions to investigate how mcDESPOT fitting would be influenced by the presence of a bound-pool, assuming $k_{FS}$ = 0 and $k_{B}$ = $k_{BF}$ = $k_{BS}$. Figure 4 suggests that the apparent MWF (in Figure 2) is not the same as the true MWF, defined as $\frac{M_{0F}}{M_{0F}+M_{0S}}$, but the relationship is monotonic and relatively insensitive to changes in bound-pool fraction. It also consistently overestimates MWF, as others have observed. However, Figure 4c shows that MWF^app is strongly influenced by RF-power level, with lower $W$ leading to a closer relationship to the ground-truth.

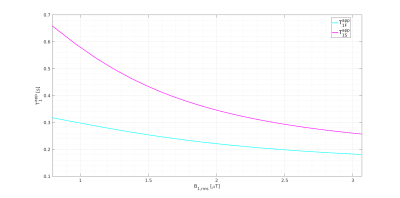
Figure 5 demonstrates that higher $B_{1,rms}$ leads to reduced apparent longitudinal relaxation times, as has been reported before.⁷ This has clear implications for the use of $T_{1}$ as a quantitative tissue parameter.

Conclusions

Acknowledgements

References

1. Deoni, S. C. L., Rutt, B. K., Arun, T., Pierpaoli, C. & Jones, D. K. Gleaning multicomponent T1 and T2 information from steady-state imaging data. Magn. Reson. Med. 2008;60:1372–1387.

2. MacKay, A. L. et al. In vivo visualization of myelin water in brain by magnetic resonance. Magn. Reson. Med. 1994;31:673–677.

3. Alonso-Ortiz, E., Levesque, I. R. & Pike, G. B. MRI-based myelin water imaging: a technical review. Magn. Reson. Med. 2015;73:70–81.

4. Zhang, J., Kolind, S. H., Laule, C. & MacKay, A. L. How does magnetization transfer influence mcDESPOT results? Magn. Reson. Med. 2015;74:1327–1335.

5. Liu, F., Block, W. F., Kijowski, R. & Samsonov, A. A. Rapid multicomponent relaxometry in steady state with correction of magnetization transfer effects. Magn. Reson. Med. 2016;75:1423–1433.

6. Henkelman, R. M., Stanisz, G. J. & Graham, S. J. Magnetization transfer in MRI: a review. NMR Biomed. 2001;14:57–64.

7. Teixeira, R. P. A. G., Price, A. N., Baburamani, A. A., Malik, S. J. & Hajnal, J. V. Robust VFA relaxometry by Continuous Saturation of Magnetization Transfer (CSMT) effects with non-selective multi-band pulses. In: ISMRM 25th Annual Meeting & Exhibition 2017.