Synopsis

We propose an approach that can reconstruct isotropic T2* Maps from undersampled data with improved accuracy by utilizing the phase information. Our approach extends the acceleration attained in Parallel Imaging(PI) to Maximum Likelihood Estimation (MLE) by imposing the exponential relaxation directly in the complex signal domain. The method was tested on a Multiecho Gradient Echo(MEGE) T2* mapping experiment in a numerical phantom and a human brain with realtime (prospective) undersampling. The approach showed that incorporating the phase information to perform coherent fitting resulted in better denoising and improved accuracy of the parametric maps.

Background

The quantification of tissue parameters from MRI data sets is emerging as a powerful tool for tissue characterization. The utilization of the technique in clinical scenarios is limited due to lengthy acquisition time. In recent years, research has focused on accelerating the acquisition by using techniques based on model-based reconstruction ^1,2, dictionary ³ and sparsity ⁴ based methods. In all these previous works, magnitude images are utilized for the exponential fitting and the phase is discarded. Whereas, the emerging Magnetic Resonance Fingerprinting (MRF) automatically works on the coherent signals ⁵. Maximum Likelihood Estimation (MLE) approach to reconstruct T2 ⁶ and T2* ⁷ maps from magnitude images have been presented but its extension to complex data has not been explored. Imposing exponential relaxation directly in the complex signal domain can be valuable for fully exploiting the acceleration attainable by Parallel Imaging (PI) in conjunction with exponential fitting in subsampled data. The purpose of this study is to ascertain the role of phase in improving the accuracy of the accelerated T2* mapping as compared to the magnitude fitting only .

Theory

For the MEGE Imaging sequence,the recorded complex signal at time $$$t_n$$$ is related to the tissue parameters $$$(\theta,t_n)$$$ as: $$x \approx f(\theta,t_n)$$

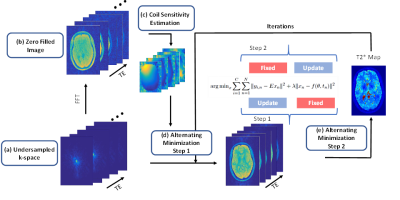
where $$$(\theta,t_n)=(\rho,T2^*,\varphi_0,b)$$$ which is modulated by exponential relaxation given by: $$f(\theta,t_n)=\rho \:exp ^{(-t_n/T2^*) + j.({\varphi_0}-{2 \pi bt_n})}$$where $$$\rho$$$ is the spin density of hydrogen atoms , $$$t_n$$$ is the echo time (TE), $$$T2^*$$$ is the spin-spin relaxation time, $$$b$$$ denotes the frequency shift in Hz and $$$\varphi_0$$$ is the constant phase due to multi channel coils. The off-resonance frequency $$$b$$$, is caused by the field inhomogeneities which can be related to the system e.g eddy currents or biological e.g. at the tissue-air interface. Given the above data model and noise characteristics, the reconstruction problem can be formulated, assuming complex Gaussian noise, as the following regularized MLE estimation problem:$$ \operatorname{arg\,min}_x \sum_{i=1}^C \sum_{n=1}^N \| y_{i,n}-E{x_n}\|^2 + \lambda \|x_n- f(\theta,t_n)\|^2 $$where $$$y_{i,n}$$$ is the acquired k-space data from the $$$ith$$$ coil and $$$nth$$$ echo , $$$E$$$ is the encoding matrix, $$$x_n$$$ is the image to be recovered ,$$$C$$$ is the total number of coils, $$$N$$$ is the number of echoes and $$$\lambda$$$ is the regularization parameter. The optimization is done iteratively using the alternating minimization with the details found in Figure (1).

Methods

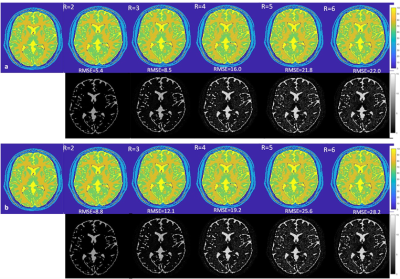
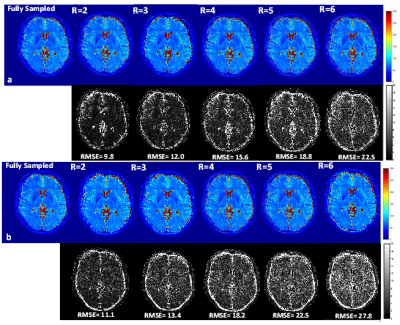
The proposed approach was tested on an anatomical brain phantom available from the Brain-Web Simulated Brain Database ⁸ and a healthy human brain. The in-vivo data was collected with an 8 channel head coil on a 1.5T clinical scanner (GE Healthcare,Waukesha, WI, USA). The data set was acquired using a 3D-enhanced fast gradient-recalled echo sequence with the following parameters (8 echoes, TR=67 ms, FOV= 156mm, 160 slices, readout Bandwidth=13.56 KHz, flip angle 15, 1.3 mm slice thickness). In addition to the fully sampled scans, undersampled datasets were acquired prospectively for different acceleration factors (R=2,3,4,5,6). The undersampled datasets were acquired using a Poisson Disk mask ⁷. T2* maps were reconstructed using both the magnitude only and the coherent phase fitting and compared with the fully sampled T2* Maps. The schematic diagram for the reconstruction using the method is shown in Figure (2). 3D coregistration and reslicing was applied using Statistical Parametric Mapping(spm-http://www.fil.ion.ucl.ac.uk/spm) to account for motion between the scans. Root Mean Squared Error (RMSE) was calculated between fully sampled and accelerated undersampled datasets to quantify the performance of the proposed method.

Results

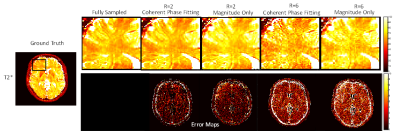
T2* maps obtained from the fully sampled data and the maps from undersampled data for the Numerical Phantom Figure 3 (a & b) and healthy volunteer Figure 4(a & b) with the magnitude and the coherent phase fitting. The RMSE with respect to the fully sampled map is given below each map. The results shows that the coherent fitting methods improves the accuracy of the T2* maps with less error (approx 20 % better) as compared to magnitude only. T2* estimation using magnitude result in over-estimation of the T2* values which is more evident in higher acceleration factors Figure (5)

Discussion & Conclusion

Acknowledgements

References

[1] Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. IEEE transactions on medical imaging. 2009 Nov;28(11):1759-69.

[2] Sumpf TJ, Uecker M, Boretius S, Frahm J. Model‐based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin‐echo MRI. Journal of Magnetic Resonance Imaging. 2011 Aug 1;34(2):420-8.

[3]Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magnetic Resonance in Medicine. 2010 Oct 1;64(4):1114-20.

[4] Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity‐promoting regularization in parametric dimension. Magnetic resonance in medicine. 2013 Nov 1;70(5):1263-73.

[5] Davies M, Puy G, Vandergheynst P, Wiaux Y. A compressed sensing framework for magnetic resonance fingerprinting. SIAM Journal on Imaging Sciences. 2014 Dec 16;7(4):2623-56.

[6] Bonny JM, Zanca M, Boire JY, Veyre A. T2 maximum likelihood estimation from multiple spin‐echo magnitude images. Magnetic resonance in medicine. 1996 Aug 1;36(2):287-93.

[7] Bano W, et al. Accelerating T2* Mapping with Maximum Likelihood Estimation (MLE) and Parallel Imaging(PI). Proc Int Soc Magn Reson. 2017, Hawaii.

[8] Aubert-Broche B, Evans AC, Collins L. A new improved version of the realistic digital brain phantom. NeuroImage. 2006 Aug 1;32(1):138-45.

[9] Lustig M, Pauly JM. SPIRiT: Iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magnetic resonance in medicine. 2010 Aug 1;64(2):457-71.