5648

MR Thermometry in Phantoms Using Bulk Magnetic Susceptibility
Scott Swanson1, Dariya Malyarenko1, and Thomas Chenevert1

1Department of Radiology, University of Michigan, Ann Arbor, MI, United States

Synopsis

We have developed a phantom for absolute temperature measurement based on the bulk magnetic susceptibility (BMS) of solutions of paramagnetic ions. This work shows that a solution of 150 mM dysprosium creates a BMS shift of approximately 0.09 ppm/°C.

Introduction

Quantitative parametric imaging requires calibration and validation of MR scanners with a quantitative phantom. Because the values of most parameters (T1, T2, diffusion, CEST effect, MT ratio) are a function of temperature, accurate knowledge of temperature is critical. We are interested in developing an MRI thermometer that allows easy imaging of absolute temperature and present here a method based on the temperature dependence of the bulk magnetic susceptibility (BMS) of solutions of paramagnetic ions.

Theory

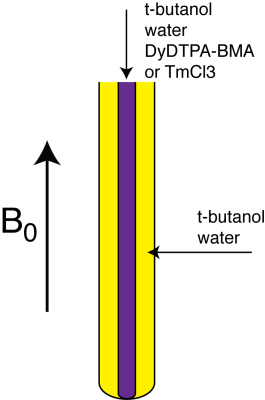
The large magnetic moments of paramagnetic ions create a sizable BMS shift between coaxial compartments of paramagnetic and diamagnetic solutions (1) (Fig1). The BMS shift can be approximated as (1,2),

$$$\Delta_x = 4 \pi [ion] s \big( \frac{\mu_{eff}}{2.84} \big) ^2 \frac{1000}{T}$$$, [1]

where $$$\Delta_x$$$ is the shift in ppm, $$$[ion]$$$ is the molar concentration, $$$s$$$ is the shape factor (1/3 for coaxial tubes), $$$\mu_{eff}$$$ is the effective magnetic moment, and T is the absolute temperature.

Methods

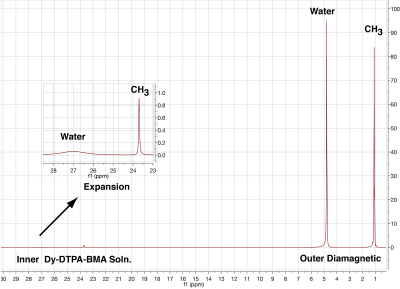
Phantoms were made in 5mm coaxial NMR tubes for study in a 11.7T Varian high-resolution NMR spectrometer (Fig1). The inner tube was tube was filled with 150 mM solutions of Dy-DTPA-BMA or TmCl3 dissolved in an aqueous solution of tertiary butyl alcohol (t-butanol). The outer tube was filled a diamagnetic t-butanol solution with equimolar water and methyl protons. Spectra were taken at 5, 15, 25, and 35°C at 11.7T and chemical shift difference between the methyl protons in the paramagnetic and diamagnetic compartments was measured. A representative spectrum of the Dy-DTPA-BMA and corresponding diamagnetic compartment is shown in Fig2.

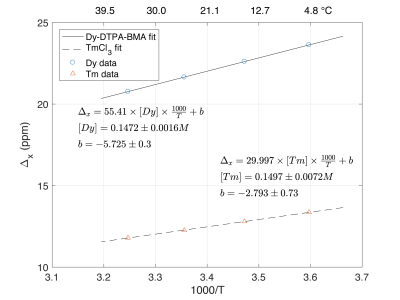
The values of $$$\mu_{eff}$$$ for dysprosium and thulium are 10.33 and 7.6, respectively. All parameters in Eq1 other that absolute concentration of paramagnetic ion are known. The BMS shift was fitted as a function of 1000/T (Eq1), allowing variation of the ion concentration and infinite temperature intercept (Fig3).

Results

Figure 2 shows 22.6 ppm shift of methyl protons due to BMS and selective broadening of water by Dy-DTPA-BMA. The relaxivity of Dy-DTPA-BMA at 11.7T was measured to be 9.1 s-1mM-1 for water and 0.148 s-1mM-1 for t-butanol methyl groups. The difference in relaxivities arises due to steric hindrance of bulky t-butanol molecules and lack of direct exchange of methyl protons with Dy (3).

Figure 3 shows that the BMS shift of Dy-DTPA-BMA and TmCl3 is accurately and precisely predicted by Eq1. The larger magnetic moment of Dy creates a larger shift and a steeper slope in Fig3 and hence a more accurate MRI thermometer. We estimate the accuracy of this method to estimate temperature in this range of temperature in 150mM Dy-DTPA-BMA solutions will be ±0.15 °C.

Discussion

These results in a high field NMR spectrometer show that the BMS in appropriate paramagnetic solutions can be used to accurately and precisely measure temperature. Other methods in MRI also measure temperature. The well known proton resonance frequency (PRF) has a sensitivity of approximately 0.01 ppm/°C (4) and shifts of methyl resonances of Tm-DOTMA has a sensitivity of approximately 0.7 ppm/°C (5). Plotting BMS as a function of temperature (rather than 1000/T as in Fig3), the sensitivity of Dy is about 0.09 ppm/°C and Tm about 0.05 ppm/°C. This is more sensitive than PRF but less sensitive that Tm-DOTMA. However, T2 of Tm-DOTMA methyl resonance is only a few ms, concentrations of 20mM or less are used, and the chemical shift is about 100ppm; creating a challenging platform for clinical imaging systems. BMS will shift the frequencies of all resonances allowing phantoms with molar concentrations of t-butanol. We are currently evaluating the feasibility of using this phantom for MR thermometry in clinical scanners.

The resonances with long T2 times in Fig. 2 (paramagnetic methyl, diamagnetic water, and diamagnetic methyl) will generate three separate images in the MR scanner and will be dispersed along the read out direction due to chemical shift. As temperature changes, the water frequency image will stay in place because the scanner will tune itself to water, diamagnetic methyl will shift right (upfield) with decreasing temperature due to PRF and paramagnetic methyl will shift left (downfield) due to BMS. These effects are seen in Fig4.

Conclusion

We have developed a phantom for in situ temperature measurement based on changes in NMR resonance frequencies due to bulk paramagnetic susceptibility. We find that 150mM solution of Dy-DTPA-BMA will shift methyl resonances in t-butanol by 0.09 ppm/°C and calculate a temperature accuracy of ±0.15°C. This phantom module is simple to construct and can be included in any phantom used for quantitative imaging where accurate knowledge of phantom temperature is required.

Acknowledgements

This research was supported by the NCI National Institutes of Health under award U01CA166104.

References

1. Chu SCK, Xu Y, Balschi JA, & Springer CS (1990) Bulk Magnetic-Susceptibility Shifts in NMR-Studies of Compartmentalized Samples - Use of Paramagnetic Reagents. Magnetic Resonance in Medicine 13(2):239-262.

2. Corsi DM, Platas-Iglesias C, van Bekkum H, & Peters JA (2001) Determination of paramagnetic lanthanide(III) concentrations from bulk magnetic susceptibility shifts in NMR spectra. Magnetic Resonance in Chemistry 39(11):723-726.

3. Aime S, Botta M, Barbero L, Uggeri F, & Fedeli F (1991) Water Signal Suppression by T2-Relaxation Enhancement Promoted by Dy(III) Complexes. Magnetic Resonance in Chemistry 29:S85-S88.

4. Ishihara Y, et al. (1995) Precise and Fast Temperature Mapping Using Water Proton Chemical-Shift. Magnetic Resonance in Medicine 34(6):814-823.

5. Hekmatyar SK, Kerkhoff RM, Pakin SK, Hopewell P, & Bansal N (2005) Noninvasive thermometry using hyperfine-shifted MR signals from paramagnetic lanthanide complexes. International Journal of Hyperthermia 21(6):561-574.


Figures

Figure 1. Arrangement of compartments in coaxial NMR tubes consisting of an outer glass tube with a diamagnetic sample and and inner glass tube with added dysprosium or thulium paramagnetic ions. All resonances in the paramagnetic sample are equally shifted by the BMS.

Figure 2. Representative spectrum of diamagnetic t-butanol and water (right) and with approximately 150mM Dy-DTPA-BMA added (left). The large Dy magnetic moment creates a large shift of both water and methyl resonances. Water T2 is significantly shortened by Dy due to proton exchange and inner sphere relaxation (3). Methyl protons of bulky t-butanol participate only in outer sphere relaxation resulting in much longer T2 times and narrower line widths. Signal intensities in the diamagnetic and paramagnetic compartments reflects the small volume of the inner (paramagnetic) coaxial tube.

Figure 3. Fit of BMS as function of 1000/T in samples of 150mM Dy-DTPA-BMA and TmCl3. The analytical nature of Eq1 allows accurate estimation of Dy and Tm concentrations (2). For our purposes, the predictable paramagnetic shifts will allow temperature estimation with an accuracy of ±0.15 °C.

Figure 4. Changes in resonance frequencies with temperature in the Dy-DTPA-BMA phantom. As temperature decreases from 35 to 15°C, frequencies of nuclei in the paramagnetic region shift downfield and the diamagnetic methyl resonance effectively moves upfield. Because water is locked on the D2O resonance, water frequency does not change. In reality, the diamagnetic methyl resonance will not change and water frequency will change according to PRF (4).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5648