5642

Information Theory Quantification of Acquisition Parameter Impact on Synthetic MRI Reconstruction Uncertainty
Drew Mitchell1, David Fuentes1, Tao Zhang2, and Ken-Pin Hwang1

1The University of Texas MD Anderson Cancer Center, Houston, TX, United States, 2GE Healthcare, Houston, TX, United States

Synopsis

We develop a mutual information-based mathematical framework to quantify the information content of a parameter space composed of several pulse sequence acquisition parameters of interest for model-based image reconstruction. We apply this framework to the signal model for a multi-contrast inversion- and T2-prepared gradient echo sequence. Mutual information between parametric map uncertainty and measured data is determined for variable acquisition parameters to characterize the performance of each acquisition. This framework allows for the strategic selection of synthetic MR acquisition parameters for specific applications and also provides a quantitative understanding of parameter space information content in an acquisition for multi-parameter mapping.

Introduction

Recent years have seen growing development of multi-parameter mapping methods, which acquire multiple contrast images in a single acquisition to map T1, T2, and PD. This reduces the scan time necessary to produce multiple series of different contrast weightings and potentially provides additional diagnostic utility. Current acquisition parameter selection is performed by utilizing a combination of simple models and experience. The purpose of this work is to develop a quantitative framework for evaluating the information content of acquisition parameter selection for multi-parameter mapping. We use this information to guide the selection of acquisition parameters for 3D QALAS (3D-quantification using an interleaved Look-Locker acquisition sequence with T2 preparation pulse)1 and evaluate their impact on parametric map reconstruction accuracy compared to conventional optimization methods.

Methods

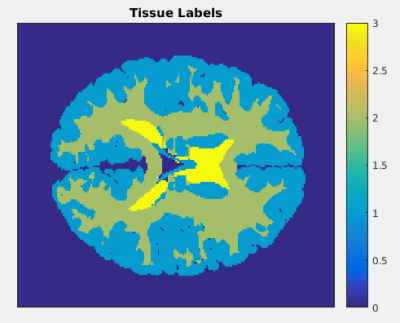
In this work, we apply the information theory-based framework to 3D QALAS acquisition.1 QALAS acquisition was simulated on a numerical phantom shown in Fig. 1 with the following parameters: flip angle = 4 degrees, matrix size = 191 x 217 x 191, repetition time = 5 ms, and number of echoes = 5. We select optimal acquisition parameters by calculating mutual information between measurements with representative noise and the signal model with uncertain parameters. Mutual information is a measure of the amount of information one random variable contains about another or the reduction in uncertainty of one random variable due to knowledge of the other. It is a special case of relative entropy between the joint distribution p(x;y) of two variables and the product of the distributions of those variables p(x)p(y). With respect to multi-parameter mapping, mutual information is a measure of how much information a measurement with a given combination of acquisition parameter values adds to the reconstruction of parametric maps. Computation of mutual information is accomplished through Gauss-Hermite quadrature. As shown in Fig. 1, tissue labels corresponding to gray matter, white matter, and cerebrospinal fluid are assumed to have normally distributed M0, T1, and T2 values. A library of signal model values is computed for each quadrature point, each point in parameter space, and each tissue type. Signal model values from the library are assigned to corresponding tissue labels during evaluation of the Gauss-Hermite quadrature.

Results

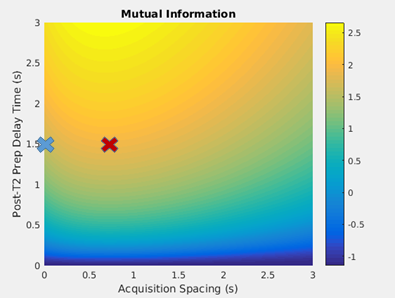
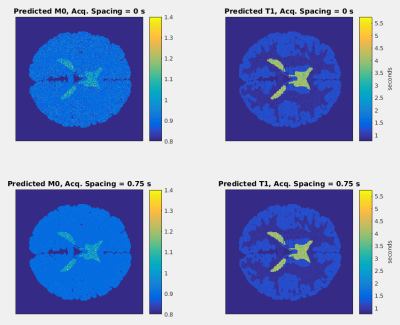
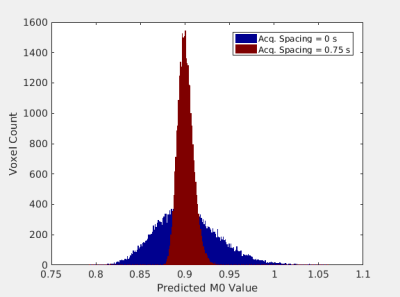
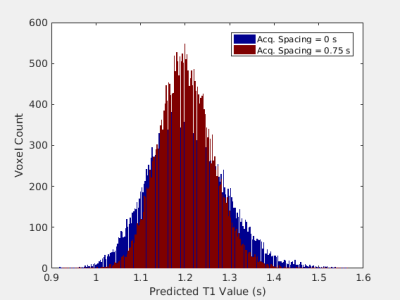
Mutual information between the parametric map parameters and the synthetic data is shown as a function of two-dimensional acquisition parameter space in Fig. 2. This parameter space is comprised of two acquisition parameters: the delay time following the T2-preparation pulse and first gradient echo acquisition and the delay time between all gradient echo acquisitions following the inversion pulse. For two combinations of these parameters corresponding to the two points in parameter space marked in Fig. 2, the generated M0 and T1 maps are shown in Fig. 3. The predicted M0 values for all voxels of gray matter from the two M0 maps are binned and displayed as histograms in Fig. 4, and the predicted T1 values for all voxels of gray matter from the two T1 maps are shown similarly in Fig. 5.

Discussion

The distributions of parametric map values resulting from a point in acquisition parameter space with greater mutual information is narrower than the distributions resulting from a point with less mutual information. These data show that parametric map uncertainty is reduced by selecting a more informative combination of acquisition parameters, as quantified by the mutual information between parametric map parameters and synthetic data. Thus, an information theory-based analysis of the construction of parametric maps in synthetic MRI utilizing mutual information may be a useful tool for quantifying and guiding selection of acquisition parameters in synthetic MRI.

Conclusion

The information theoretic analysis described in this work allows quantitative guidance of synthetic MRI acquisition parameters across multiple applications. It represents an advanced quantitative understanding of the relationship between acquisition parameters and parametric map reconstruction uncertainty. The major contribution of this research is the quantitative assessment of the impact of acquisition parameter selection on reconstructed parametric map uncertainty, which is currently only heuristically understood. This guides an optimized selection of acquisition parameters for a given application. It may also be useful in the evaluation of reproducibility in clinical settings. This mutual information framework could prove valuable in model-based reconstruction for several other modalities. It is applicable to any other method with an acceptable model, including most MR pulse sequences and reconstructions. The physics model will determine the prior and posterior statistics, and the mutual information framework can be used to similarly determine the most informative data to be used in reconstruction.

Acknowledgements

Research support was provided in part by GE Healthcare.

References

1. Kvernby, S., Warntjes, M. J., Haraldsson, H., Carlhall, C. J., Engvall, J., & Ebbers, T. (2014). Simultaneous three-dimensional myocardial T1 and T2 mapping in one breath hold with 3D-QALAS. J Cardiovasc Magn Reson, 16, 102. http://doi.org/10.1186/s12968-014-0102-0

2. Zhang, T., Pauly, J. M., & Levesque, I. R. (2015). Accelerating parameter mapping with a locally low rank constraint. Magnetic Resonance in Medicine, 73(2), 655–661. http://doi.org/10.1002/mrm.25161

Figures

Tissue label map used for the generation of realistic synthetic data. Label 1 corresponds to gray matter, 2 corresponds to white matter, and 3 corresponds to cerebrospinal fluid. To generate synthetic data, normally distributed values centered about literature M0, T1, and T2 values are assigned to the each respective tissue type. With these values and the selected acquisition parameter values as input, the signal model is used to create synthetic measurements, which are then corrupted by normally distributed noise to simulate measurement data.

Mutual information between parametric map parameters and synthetic measurement data in two-dimensional acquisition parameter space. The acquisition parameters are the delay time following the T2-preparation pulse and first gradient echo acquisition (Post-T2 Prep Delay Time) and the delay time between all gradient echo acquisitions following the inversion pulse (Acquisition Spacing). The red marker represents a relatively more informative point in parameter space compared to the blue marker, which is a less informative location.

Parametric maps of M0 and T1 generated from synthetic measurement data. The parametric maps result from the solution of the inverse problem which optimally fits the modeled signal to the synthetic measurement data. The top left and top right maps use acquisition parameters from a more informative point in parameter space (denoted by the red marker in Fig. 2). The bottom left and bottom right maps use acquisition parameters from a less informative point in parameter space (denoted by blue marker in Fig. 2).

Histograms of predicted M0 values for each voxel of gray matter. The red histogram represents data from the construction of synthetic measurements and generation of parametric maps using acquisition parameters from a more informative point in parameter space (denoted by the red marker in Fig. 2). The blue data represents data using acquisition parameters from a less informative point in parameter space (denoted by blue marker in Fig. 2).

Histograms of predicted T1 values for each voxel of gray matter. The red histogram represents data from the construction of synthetic measurements and generation of parametric maps using acquisition parameters from a more informative point in parameter space (denoted by the red marker in Fig. 2). The blue data represents data using acquisition parameters from a less informative point in parameter space (denoted by blue marker in Fig. 2).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5642