Synopsis

To overcome the shortcomings of curve fitting to quantify perfusion properties, a dictionary matching approach like that used in magnetic resonance fingerprinting is proposed. This dictionary matching approach could be used for any DCE application or model, but is demonstrated and validated here for a dual-input single-compartment model of liver DCE-MRI data. The dictionary matching method provides similar results to the curve fitting method while being simpler to implement and dramatically faster.

Introduction

Dynamic contrast-enhanced (DCE) MRI data can be combined with pharmacokinetic models to estimate perfusion properties. Typically a curve fitting algorithm is used to find the best fit to solve for these perfusion properties^1,­2,3. However, this approach has drawbacks. Curve fitting has many configuration options including initial values, algorithm choice, tolerances and cost functions used for the fit. Additionally, curve fitting is slow and can require hours to generate perfusion maps for a single 3D DCE-MRI liver acquisition⁴.

To overcome major shortcomings of curve fitting, we propose using a dictionary matching approach analogous to that used in Magnetic Resonance Fingerprinting⁵. This approach requires minimal configuration and can be dramatically faster than curve fitting. This approach was tested in simulation and validated with in vivo data to estimate liver perfusion properties.

Methods

Although a dictionary approach could be used for any DCE application, liver DCE-MRI data were used with a dual-input single-compartment (DISC) model (equation 1) for this first validation:

$$ \frac{dC_L(t)}{dt} = k_{1a} C_a(t) + k_{1p} C_p(t) - k_2 C_L(t) $$

The rate constants ($$$k_{1a}$$$, $$$k_{1p}$$$, $$$k_2$$$ ) are commonly reformulated as the arterial fraction (AF), distribution volume (DV), and mean transit time (MTT) as described in [1]. $$$C_a$$$ and $$$C_p$$$ were generated by placing regions-of-interest in the aorta and portal vein, respectively, and converting signal intensity to concentration.

Here, the performance and accuracy of curve fitting is compared to the proposed dictionary matching approach. MATLAB’s lsqcurvefit was used to fit the AF, DV, and MTT with a step tolerance of 1×10⁻¹⁶, a function tolerance of 1×10⁻¹⁰, and a minimum gradient change of 0.001. Fitting bounds were set to 0–1, 0–1, and 1–100 with initial parameter estimates of 0.2, 0.2, and 10 for AF, DV, and MTT, respectively.

For matching, subject-specific dictionaries were created with ranges of 0–1 and 1–100 with step sizes of 0.01 and 1 for AF and MTT, respectively. Each permutation of AF and MTT was used with the arterial and portal venous input functions to calculate a liver tissue contrast concentration curve from the DISC model. 3D DCE-MRI data were converted to contrast concentrations using the spoiled gradient echo signal equation. The acquired concentration curves were matched to the dictionary by identifying the maximum correlation coefficient. From this dictionary index, the perfusion properties used to generate the entry were obtained. DV is subsequently calculated as a scaling term.

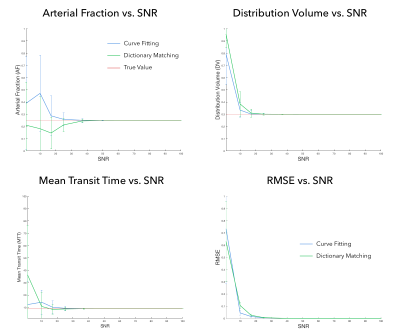
Both methods were compared using Monte Carlo simulations. An idealized contrast concentration curve was created from the DISC model using idealized input functions and AF of 0.25, DV of 0.30, and MTT of 9s². From this curve, 100 additional curves were generated by adding noise at eight SNR levels between 1 and 100. The root mean square error (RMSE) between the estimated curve from each method and the idealized curve was calculated at each SNR.

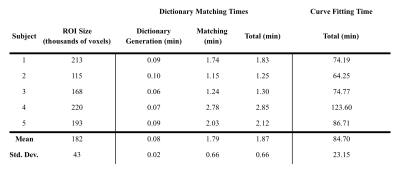
Curve fitting and dictionary matching were further applied to 3D DCE-MRI acquisitions from 5 subjects (2 volunteers, 2 patients with metastatic adenocarcinoma, and 1 patient with hepatocellular carcinoma) using a highly accelerated 3D spiral acquisition and a through-time spiral GRAPPA reconstruction². The RMSE was calculated between corresponding perfusion maps from each method to assess similarity.

Results

For the simulations, Figure 1 plots each estimated perfusion property quantified by the curve fitting and dictionary matching methods against each SNR from the Monte Carlo simulations as well as the RMSE between the estimated curves and the ideal curve against each SNR.

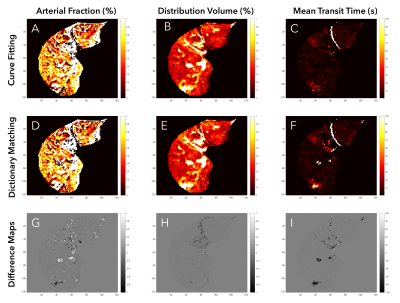
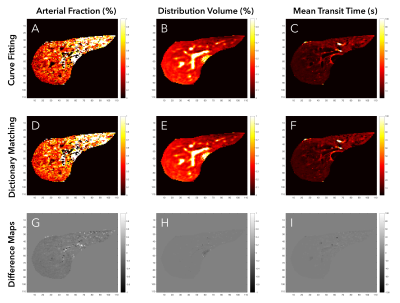
Figures 2 and 3 show single-slice perfusion and difference maps using the curve fitting and dictionary matching methods for a patient with hepatocellular carcinoma and a healthy volunteer, respectively. For the 5 subjects, the mean RMSE between methods for the AF, DV, and MTT perfusion maps were 0.06, 0.02, and 1.74, respectively. The dictionary matching required 1.9 minutes as compared to 1.4 hours for curve fitting. Perfusion quantification times for all subjects are detailed in Table 1.

Conclusion

Acknowledgements

Research support: NIH grant 1R01DK098503 and Siemens Healthineers

References

1. Materne R, Van Beers BE, Smith AM, et al. Non-invasive quantification of liver perfusion with dynamic computed tomography and a dual-input one-compartmental model. Clinical Science. 2000;99(6):517. doi:10.1042/CS20000080.

2. Chen Y, Lee GR, Wright KL, et al. Free-Breathing Liver Perfusion Imaging Using 3-Dimensional Through-Time Spiral Generalized Autocalibrating Partially Parallel Acquisition Acceleration. Investigative Radiology. 2015;50(6):367-375. doi:10.1097/RLI.0000000000000135.

3. Bultman EM, Brodsky EK, Horng DE, et al. Quantitative hepatic perfusion modeling using DCE-MRI with sequential breathholds. J Magn Reson Imaging. 2013;39(4):853-865. doi:10.1002/jmri.24238.

4. Wang H, Cao Y. GPU-accelerated voxelwise hepatic perfusion quantification. Phys Med Biol. 2012;57(17):5601-5616. doi:10.1088/0031-9155/57/17/5601.

5. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187-192. doi:10.1038/nature11971.