5636

High Resolution T1 quantification from golden-angle radial 3D acquisitions.
Oliver Maier1, Matthias Schloegl1, Jasper Schoormans2, Bram Coolen2, Tobias Block3,4, Thomas Benkert3,4, Gustav Strijkers2, and Rudolf Stollberger1

1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Department of Biomedical Engineering & Physics, Academic Medical Center, Amsterdam, Netherlands, 3Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States, 4Bernard and Irene Schwartz Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States

Synopsis

A model-based reconstruction approach is presented that allows time efficient encoding of radial data for high resolution 3D T1 quantification e.g. (256x256x52, 1mm3, tscan=96s) by exploiting structural similarities in 3D and between different parameter maps. The proposed method employs a 3D TGV-Frobenius regularization to achieve high quality parameter maps from 3D VFA and 3D IRLL data. A dedicated reconstruction framework, consisting of an iteratively-regularized Gauss-Newton algorithm combined with a Primal-Dual splitting is employed to solve the optimization problem. Reconstructed parameter maps exhibit high SNR and no residual streaking artifacts while reconstructed T1 values agree well with reported values from literature.

Introduction

Quantitative MRI is considered to play an important role in precision medicine. Challenges for clinical applications include the prolonged scan time and partial volume effects, in particular for focal lesions. Therefore, isotropic voxel volumes of 1mm3 with reasonable scan time are highly desirable. This can be achieved by exploiting structural information in quantitative MRI, combined with model-based reconstruction of incomplete k-space data. Most existing model-based reconstruction techniques[1,2] utilize gradient based optimization routines, which require a smooth cost-function. Thus, only basic regularization techniques can be employed, which do not take advantage of structural information in the parameter maps. Aim of the present work was to reconstruct accurate high-resolution T1 maps from 3D radial data, acquired within as few as 96s. To this end, we propose a Total-Generalized-Variation (TGV) based regularization[3,4] combined with a Frobenius-norm to exploit structural information in each map as well as shared features between the parameters of interest. The performance of the proposed algorithm is shown for 3D-T1 quantification from golden-angle Radial-VIBE (RAVE)[13] data, as well as for radial stack-of-stars Inversion-Recovery Look-Locker (IRLL)[10] data.

Methods

The initially non-linear problem is linearized around point xk following the Gauss-Newton approach. This leads to a linear forward operator (DA), combining the linearized model equation and the MR sampling operator, which contains coil sensitivities and non-uniform Fourier transformation. Constant terms, stemming from the linearization, are precomputed and combined with the measured data (dk). A L2-discrepancy between DA and dk composes the data-fidelity term. Combined with TGV-Frobenius regularization directly on the unknown parameters and a L2-step size penalty, this leads to the following optimization problem:

$$\frac{1}{2}\|DAx-d_k\|^2_2+\lambda\,TGV_F(x)+\frac{\gamma}{2}\|x-x_k\|_2^2$$

The linearized problem is solved using a PD-algorithm[5,6] due to the TGV regularization. The linearization process is iteratively repeated to find an optimal solution. Regularization parameters are adapted after every linearization to avoid over-regularization. Normalization of input data is performed to obtain regularization parameters independent of the amount of acquired data. Furthermore, SVD-based coil compression, followed by coil-sensitivity estimation[11] is performed.

The variable-flip-angle (VFA)[7,8,9] data has been acquired on a 3T Siemens Skyra scanner using a radial stack-of-stars 3D sequence (RAVE) with golden-angle ordering[13] and B1+ correction[12].

IRLL data was measured on a 3T Philips Ingenia with a radial stack-of-stars 3D sequence, encoding one radial stack at a time with golden-angle ordering, so that spokes can be grouped into an arbitrary number of spokes/time-fame during postprocessing. Additional, a B1+ estimation sequence[16] was employed and correction of the acquired trajectory was performed[14].

The accuracy of the proposed method is demonstrated by comparing a fully-sampled phantom measurement to reconstruction from 21 spokes for VFA data.

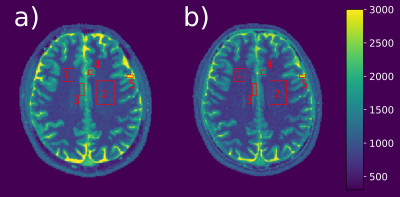
IRLL data is then compared to a 2D-Cartesian IRLL scan corresponding to the center of the 3D volume, reconstructed using a pixel-wise fitting routine.

Results

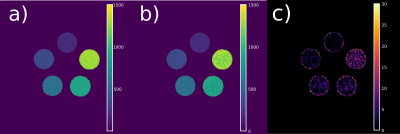
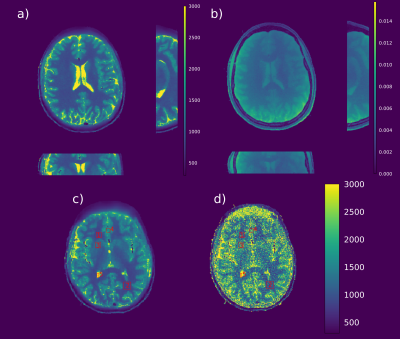
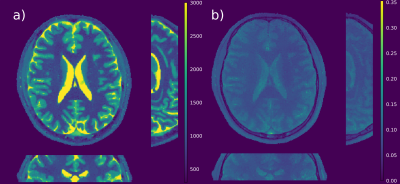
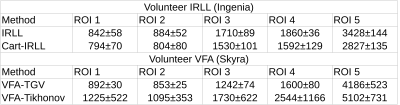
T1 maps of a MR phantom (Figure 1) reconstructed from fully-sampled VFA data (1a) are compared to undersampled acquired VFA data (1b); the relative error between the maps is given in percent (c). Figure 2 shows the reconstruction of a 3D volume using 21 spokes from in-vivo VFA head measurements with the proposed method (a,b,c) compared to standard regularization (d). In-vivo results for IRLL measurements are shown in Figure 3. Selected ROIs for IRLL data (4a) are compared to a fully-sampled 2D-Cartesian reference scan (4b). Table 1 shows T1 values for selected ROIs and the used methods.

Discussion

T1 values are in good agreement between undersampled and fully-sampled reference data. In-vivo parameter maps exhibit sharp edges and are free of residual streaking-artifacts despite high acceleration compared to noisy reconstructions using standard Tikhonov regularization. Furthermore, T1 values for selected ROIs are in-line with reported values from literature[15]. Compared to Cartesian, the higher T1 in radial IRLL scans may stem from the nature of data acquisition and reduced partial volume artifacts due to 3D isotropic resolution. In radial scans, every spoke contributes the same amount to the overall image contrast, a distinct difference to Cartesian scans. This can be included in the model by calculation of a mean over spokes/frame in contrast to the Cartesian case, where an apparent echo spacing has to be used.

Conclusion

The proposed algorithm is able to recover T1 maps from highly undersampled radial data by exploiting structural similarities in the imaging volume and across parameters. This enables obtaining high quality T1 maps within measurement times of 1.5s/slice for VFA and 8s/slice for IRLL. While the approach can be used for different T1 mapping methods without changes to the algorithm, strong variations in the noise level require minor adjustments of the TGV regularization parameter to generate optimally regularized images.

Acknowledgements

This work was funded by the Austrian Science Fund "SFB F3209-18"; "HTI:Tech for Med" (ABT08-22-T-7/2013-13); NVIDIA Corporation Hardware grant support

References

1. Block KT, Uecker M, Frahm J. Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI. IEEE Traansactions on Medical Imaging, Vol. 28, No. 11, November 2009

2. Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imag 2011; 34(2):420–428

3. Chambolle A, Caselles V, Novaga M, Cremers D, Pock T. An introduction to Total Variation for Image Analysis. 2009

4. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med 2011; 65(2):480-91.

5. Chambolle A, and Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision 2011; 40(1):120--145.

6. Maltisky Y, Pock T. A first-order primal-dual algorithm with linesearch. arXiv:1608.08883v1 [math.OC]

7. Homer J, Beevers MS. Driver-equilibrium single-pulse observation of T1 relaxation. A re-evaluation of a rapid “new” method for determining NMR spin-lattice relaxation times. J Magn Reson 1985; 63: 287--297.

8. Deoni SC, Rutt BK, and Peters TM. "Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state." Magn Reson Med 2003; 49: 515-526.

9. Deoni SC, Peters TM, Rutt BK. High-resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn Reson Med 2005; 53: 237–241.

10. Henderson E, McKinnon G, Lee TY, Rutt BK. A Fast 3D Look-Locker Method for volumetric T1 Mapping. Magn Reson Imaging. 1999 Oct;17(8):1163-71.

11. Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion—joint estimation of coil sensitivities and image content. Magn. Reson. Med. 2008; 60:674-82

12. A. Lesch, M. Schloegl, M. Holler, and R. Stollberger. Highly accelerated Bloch-Siegert B1+ mapping using variational modeling. In Proc Intl Soc Mag Reson Med, volume 24, page 1875, 2016.

13. Block K.T., Chandarana H., Fatterpekar G., et al. MAGNETOM Flash (2013); 5:6-11.

14. Moussavi, Amir, et al. "Correction of gradient‐induced phase errors in radial MRI." Magnetic resonance in medicine 71.1 (2014): 308-312.

15. Stikov N., Boudreau M., Levesque I.R., Tardif C.L., Barral J.K., Pike G.B.; On the Accuracy of T1 Mapping: Searching for a Common Ground. Magn. Reson. Med. 2015; 73:514-522

16. Nehrke K. and Boernert P. DREAM—a novel approach for robust, ultrafast, multislice B1 mapping. Magnetic resonance in medicine 68.5 (2012): 1517–1526

Figures

Figure 1: Relative difference in percent (c) between T1 maps from fully sampled data (a) compared to 21 measured spokes (b). Data was acquired with a 256x256x12 matrix and 1x1x3mm3 voxel size. Measurement parameters of the RAVE sequence were: TR = 5ms, TE = 2.46ms, Flip angles = 1,2,3,4,5,6,7,9,11,13°, Bandwidth = 380Hz/pixel, samples per spoke = 512, 40 calibration lines. Total acquisition time 18s (a) vs 10 min (b).

Figure 2: 3D T1 (a) and pseudo proton density (M0) (b) map from a healthy volunteer acquired with the VFA approach. Data was acquired with a 256x256x52 matrix and 1mm3 voxel size. Measurement parameters of the RAVE sequence were: TR = 5ms, TE = 2.46ms, Flip angles = 1,2,3,4,5,6,7,9,11,13°, Bandwidth = 380Hz/pixel, samples per spoke = 512, 21 spokes acquired, 1.23 slice oversampling. Total acquisition time 96s. Reconstruction of the inner 38 slices to avoid slab profile effects. The lower part shows a comparison of the proposed TGV-Frobenius (c) and standard Tikhonov (d) regularization.

Figure 3: T1 (a) and M0 (b) maps of a 3D volume acquired with a IRLL sequence. Scan parameters of the radial IRLL-sequence were as follows: delay after inversion (minTI) = 14.3ms, 731 spokes with a TR of 6ms, flip angle = 5°, undisturbed recovery of 3600ms after read out; 8s acquisition time per encoded star; total acquisition time = 8 min, acquisition matrix of 212x212x40 with 1mm3 isotropic resolution and 1.5 slice oversampling. Reconstruction is performed using 21 spokes and 25 time frames.

Figure 4: Comparison between radially (a) and 2D Cartesian (b) acquired IRLL data. T1 map (a) corresponds to the center slice of Figure 3. Cartesian data was acquired as single slice in 2D with 1x1x2.5mm3 resolution and 212x212 pixels with the following parameters: minTI = 14.3ms, no. k-lines per segment = 8, no. segements = 26, TR = 10ms; Effective echo time = 80ms and 54.3ms delay at the beginning. 50 time points where acquired with an undisturbed delay of 2230ms. Total acquisition time 2min42s. Slices are not registered with little movement between the scans.

Table 1: Comparison of T1 values for selected ROIs in gray matter, white matter and CSF. ROI numbering corresponds to ROIs in Figure 2 and Figure 4. All T1 values are in agreement with reported values from literature [15].

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5636