5634

Rapid B1 mapping based on the Bloch-Siegert shift using a single offset frequency and multi-echo readout
Nadège Corbin1, Julio Acosta-Cabronero1, Oliver Josephs1, Nikolaus Weiskopf1,2, and Martina F Callaghan1

1Functional Imaging Laboratory (FIL) & Wellcome Center for Human Neuroimaging, UCL Institute of Neurology, London, United Kingdom, 2Department of Neurophysics, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany

Synopsis

The advance towards in vivo histology benefits greatly from the quantification of specific physical parameters1. The longitudinal relaxation rate (R1) has proven a reliable surrogate for myelination, facilitating investigation of the relationship between brain microstructure and function in vivo2–5. R1 maps can be estimated by combining spoiled gradient-echo volumes, acquired with variable flip angles, and calibration data correcting for flip angle inhomogeneities. The Bloch-Siegert shift (BSS) approach6 is a relatively time-efficient method that allows the calibration data to be acquired with an identical gradient-echo readout thereby matching distortions across all data needed to map R1. However, it requires data to be acquired at two off-resonance frequencies to remove B0 dependence up to second order and suffers from high specific-absorption-rate (SAR). Here, we investigate a modified BSS-based B1+ mapping approach that aimed to overcome these shortcomings by using a single offset frequency and a multi-echo readout.

Introduction

Accurate quantification of key physical parameters, such as R1, necessitates B1+-mapping to account for flip angle inhomogeneity but must be time-efficient in order to facilitate high-resolution, whole-brain mapping in feasible scan times. The Bloch-Siegert shift (BSS)6 is a relatively time-efficient B1+-mapping method that allows calibration data to be acquired with the same spoiled gradient-echo readout as used in variable flip angle R1 mapping approaches, thereby additionally matching spatial distortions. An off-resonance RF pulse is applied after excitation that induces a B1-dependent phase7. The phase difference between two acquisitions with opposite off-resonance frequencies, i.e. ±ωRF, isolates the BSS phase and removes offsets and B0 inhomogeneity dependence, up to second order. Here, we investigate the possibility of using a single off-resonance frequency to halve the acquisition time or facilitate SAR management, particularly relevant for UHF, without increasing scan time.

Methods

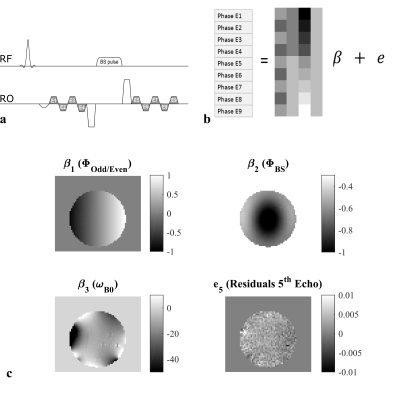
The spatially-specific BSS, ΦBS caused by an RF pulse at off-resonance frequency ωRF in the presence of field inhomogeneity ωB0 is given by: $$\Phi_{BS}(x)=B_{1,peak}^2(x)\int_{0}^{T}\frac{(\gamma B_{1,normalized}(t))^2}{2(\omega_{B0}(x)-\omega_{RF})}dt = B_{1,peak}^2*K_{BS}(x) $$

Unlike the classic dual-offset BSS method6, here ΦBS is estimated from a single off-resonance frequency via a General Linear Model (GLM) applied to the phase data from a multi-echo readout (Fig1a). The design matrix includes regressors modelling (Fig1b):

1. the variation between even and odd echoes due to the bipolar readout;

2. the effect of the Bloch-Siegert pulse;

3. phase accrued with TE due to B0 inhomogeneities;

4. any common phase offset.

Given this formalism, the GLM also estimates ωB0 making the KBS term spatially-specific (whereas it is constant in the classic BSS approach). In this case, the B1+ estimation is theoretically completely independent of B0 inhomogeneity. Whereas the classic BSS method benefits from higher ωRF to minimise sensitivity to B0 inhomogeneity, this approach should be independent of B0. This multi-echo BSS (MEBSS) approach was tested in a gel phantom and in vivo using a single-channel transmit-receive head coil at 3T (Siemens Prisma). A 3D spoiled gradient-echo acquisition was used with an excitation flip angle of 12° and TR=60ms (50ms in phantom) with 4mm isotropic resolution. The BSS was induced by a 2ms-long Fermi pulse with 350° (320° in phantom) flip angle with four echoes (TE=2.30:2.30:9.20ms) acquired before (Fig1a) and five after (TE=14.98:2.30:24.18ms). In order to compare the MEBSS approach with the classic BSS approach, the data were acquired with interleaved positive and negative off-resonance frequencies with ωRF=±2, 4 and 8kHz. All echoes from a single offset frequency were used to calculate B1+ maps using the MEBSS approach whereas the first echo after the Bloch-Siegert pulse combining both off-resonance frequencies was used to estimate the B1+ map with the classic approach. A 3D median filter (kernel 5x5x5 voxels) was applied to all maps. Reference B1+ maps were acquired using a spin-echo/stimulated-echo method8,9 with a modified protocol for use with the single channel coil.

Results

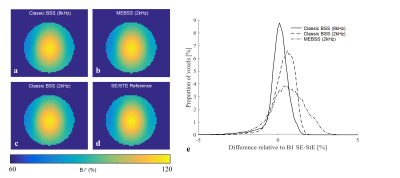
B1+ maps from the phantom (Fig.2a-d) illustrate the concordance of the different mapping methods. Quantitative histogram analysis indicates excellent agreement between the reference method and the classic BSS approach with ωRF= 8kHz, but greater variance and bias for the classic approach when ωRF is reduced to 2kHz. This can be expected due to increased sensitivity to B0 inhomogeneity. While the variance is larger for the proposed MEBSS approach, and bias still exists, the error remains less than 3% while only requiring half the scanning time.

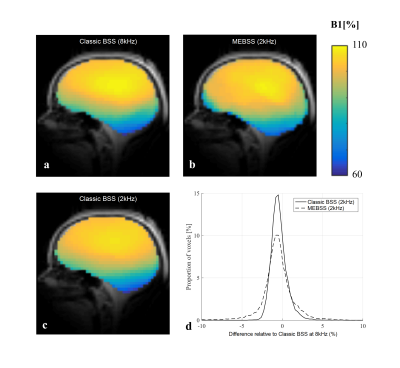
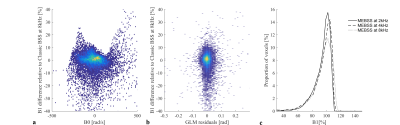
In vivo, the spin-echo/stimulated-echo did not perform well because of artefacts due to the low bandwidth in the phase-encoded direction (due to a modified protocol without parallel imaging). Therefore, the dual-offset approach with ωRF=±8kHz was taken as reference. The proposed MEBSS B1+ maps were again of good quality. Although the relative error was greatest for this approach, it remained <5% (Fig.3). The error in the MEBSS B1+ maps did not correlate with B0 inhomogeneity (Fig.4a) or model residuals (Fig.4b). However, a theoretically unexpected dependence on ωRF was observed empirically (Fig.4c).

Discussion

While this novel MEBSS approach halved the acquisition time and produced qualitatively good B1+ maps, the errors were greater than the classic approach. This may be due to the fact that the Bloch-Siegert phase is halved when using only one ωRF, thereby reducing contrast. Furthermore, unlike in the dual-offset approach where other phase components cancel out, with this formalism all other sources of phase variation must be accurately modelled. However, the errors observed did not correlate with either field inhomogeneity or model residuals. An unexpected source of bias was the choice of offset frequency: the bias increased with increasing ωRF, the opposite trend to the classic approach. Future work will further explore the potential sources of error and this dependence of MEBSS on ωRF.

Acknowledgements

MFC is supported by the MRC and Spinal Research Charity through the ERA-NET Neuron joint call (MR/R000050/1). The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome [203147/Z/16/Z].

References

1. Weiskopf, N., Mohammadi, S., Lutti, A. & Callaghan, M. F. Advances in MRI-based computational neuroanatomy: from morphometry to in-vivo histology. Curr. Opin. Neurol. 28, 313–22 (2015).

2. Dick, F. et al. In vivo functional and myeloarchitectonic mapping of human primary auditory areas. J. Neurosci. 32, 16095–105 (2012).

3. Carey, D., Krishnan, S., Callaghan, M. F., Sereno, M. I. & Dick, F. Functional and Quantitative MRI Mapping of Somatomotor Representations of Human Supralaryngeal Vocal Tract. Cereb. Cortex 1–14 (2017). doi:10.1093/cercor/bhw393

4. Lutti, A., Dick, F., Sereno, M. I. & Weiskopf, N. Using high-resolution quantitative mapping of R1 as an index of cortical myelination. Neuroimage 93 Pt 2, 176–88 (2014).

5. Sereno, M. I. et al. Mapping the human cortical surface by combining quantitative T(1) with retinotopy. Cereb. Cortex 23, 2261–2268 (2013).

6. Sacolick, L. I., Wiesinger, F., Hancu, I. & Vogel, M. W. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 63, 1315–22 (2010).

7. Bloch, F. & Siegert, A. Magnetic Resonance for Nonrotating Fields. Phys. Rev. 57, 522–527 (1940).

8. Lutti, A. et al. Robust and Fast Whole Brain Mapping of the RF Transmit Field B1 at 7T. PLoS One 7, e32379 (2012).

9. Lutti, A., Hutton, C., Finsterbusch, J., Helms, G. & Weiskopf, N. Optimization and validation of methods for mapping of the radiofrequency transmit field at 3T. Magn. Reson. Med. 64, 229–38 (2010).

Figures

Figure 1: The sequence diagram of the 3D gradient echo acquisition is illustrated in (a). Four echoes were acquired prior to, and five echoes after, the Bloch-Siegert pulse, which was flanked by crushers to destroy any inadvertent on-resonance excitation. A GLM was used to model the phase variation across echo times (b). The model coefficients obtained with the phantom (c) highlight phase accrued due to alternating readout (RO) polarity, the Bloch-Siegert Shift and B0 field inhomogeneity.

Figure 2: Exemplar planes through the B1+ maps produced by the classic BSS method (a, c), multi-echo BSS (b) and reference spin-echo/stimulated-echo (d) methods illustrating the quality of, and agreement between, the approaches. Quantitative histogram analysis indicates excellent agreement between the reference method and the classic BSS approach with an off-resonance frequency of 8kHz, but greater error when the off-resonance frequency is reduced to 2kHz. This would be expected due to increased sensitivity to B0 inhomogeneity. While the error is largest for the proposed MEBSS approach and the bias is still present, it still remains less than 3% while only requiring half the scanning time.

Figure 3: Exemplar planes through the in vivo B1+ maps, overlaid on the magnitude image to provide anatomical orientation. While there is qualitative agreement between the approaches, there is greater discrepancy in inferior-frontal regions. Both the classic BSS approach with ωRF=±2kHz and the MEBSS method show a small bias with respect to the classic BSS method with ωRF=±8kHz (used as the reference in vivo because of the poor quality of the spin-echo/stimulated echo approach). The error is larger for the MEBSS method but remains less than 5%.

The error observed with the MEBSS approach is not correlated with B0 inhomogeneities (a) or model residuals (b). However, the observed bias increases with increasing ωRF such that the estimated B1+ amplitude increases with increasing ωRF.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5634