5623
Approximation of Contrast Source for Fast Integral-Based MR-EPT and the Calculation of Incident Electric Field1ITEE, The University of Queensland, Brisbane, Australia, 2South China University of Technology, Guangzhou, China
Synopsis
Integral-based Magnetic Resonance Electrical Properties Tomography (MR-EPT), has seen rapid development in recent years. Compared with differential-based MR-EPT methods, integral-based methods are less sensitive to measurement noise and free from boundary conditions. The integral-based MR-EPT methods rely on the global convolution between the Green function and the contrast source, and also require the knowledge of incident fields. This study investigates a novel method to approximate the contrast source, and then utilizes this approximation to calculate the incident electric fields.
Introduction
Integral-based MR-EPT faces several practical challenges. Among these problems, the slow convergence rate and the difficulty in accurate acquisition of incident fields are two critical issues which prevent this method from being widely used. Reconstruction of contrast source is an essential task in integral-based MR-EPT methods. To solve the inverse problem with iterative methods, appropriate initialization of contrast source is necessary. Conventional initialization methods lead to slow convergence rate 2-3. For example, in three-dimensional scenario, reconstruction can take hours 3. This study investigates a novel approximation of contrast source based on the differential Maxwell’s equation. This approximation provides an accurate initialization of the contrast source, thereby significantly improving the convergence rate compared with conventional initialization methods. Furthermore, this approximation can be used to calculate the incident electric field which is required in integral-based methods and usually can only be obtained from simulations 1-3. Owing to the loading effect, the simulated incident field is different from those in practice particularly when the RF-coils are re-tunned and re-matched to the loading conditions. The calculated incident E-field takes these factors into account thus improving accuracy of integral-based MR-EPT.Method
An essential task of integral-based MR-EPT algorithm is the calculation of contrast source $$${\bf{w}}$$$. The Ampere’s Law shows that $$$\triangledown\times{{\bf{H}}}=\left[\sigma+i\omega\varepsilon_{r}\varepsilon_b\right]{\bf{E}}$$$, where $$${\varepsilon_b}$$$ is the background permittivity. By rearranging this formula, we arrive at $$$i\frac{\triangledown\times{\bf{H}}}{\omega\varepsilon_b}=\Big[\frac{i\sigma}{\omega\varepsilon_b}-\varepsilon_r\Big]{\bf{E}}$$$. The right side of this rearranged formula is remarkably similar to the expression of contrast source used in integral-based EPT methods $$${\bf{w}}=\Big(\varepsilon_r-\frac{i\sigma}{\omega\varepsilon_b}-1\Big){\bf{E}}$$$, where $$$\cal{X}=\Big(\varepsilon_r-\frac{i\sigma}{\omega\varepsilon_b}-1\Big)$$$ is recognized as the contrast function. Considering that the relative permittivity $$${\varepsilon_r}$$$ of most body tissues are much larger than 1, the real part of $$${\cal{X}}$$$, $$$real(\cal{X})=\varepsilon_r-1$$$, is an accurate approximation of relative permittivity, namely, $$$\varepsilon_r\approx\varepsilon_r-1=real(\cal{X})$$$, while $$${\bf{w}}$$$ can be derived from $$$-i\frac{\triangledown\times{\bf{H}}}{\omega\varepsilon_b}\approx{\bf{w^{\it{init}}}}$$$. To calculate the curl of $$${\bf{H}}$$$, the $$${H_x}$$$ and $$${H_y}$$$ can be calculated from $$$B_1^{\pm}$$$ mapping, and if $$${H_z}$$$ can be initially assumed as 0. This assumption is largely valid for surface loop coil 4 and most of the current coil designs. Based on this approximation, $$${w_z}$$$ can be calculated accurately, whereas $$${w_x}$$$ and $$${w_y}$$$ can be estimated with the lack of $$${H_z}$$$ component. After $$${\bf{w}}^{\it{init}}$$$ is initialized, the $$${H_z}$$$ component can be subsequently calculated using the integral-based method 5, thus accurate reconstruction of $$${\bf{w}}$$$ can be achieved. Assuming that the operator $$$\cal{H_{\cal{D}}}$$$ maps the contrast source to the scattered magnetic field 5, the incident electric fields can be calculated as $$\begin{cases}E_x^{\it{inc}}=\frac{1}{i\omega\varepsilon_b}\Big[\frac{\partial(\cal{H_{\cal{D}}}{\bf{w^{\it{init}}}})_z}{\partial{y}}-\frac{\partial\big(H_y-({\cal{H_{\cal{D}}}{\bf{w^{\it{init}}}}})_y\big)}{\partial{z}}\Big]\\E_y^{\it{inc}}=\frac{1}{i\omega\varepsilon_b}\Big[\frac{\partial\big(H_x-(\cal{H_{\cal{D}}}{\bf{w^{\it{init}}}})_x\big)}{\partial{z}}-\frac{\partial({\cal{H_{\cal{D}}}{\bf{w^{\it{init}}}}})_z}{\partial{x}}\Big]\\E_z^{\it{inc}}=\frac{1}{i\omega\varepsilon_b}\Big[\frac{\partial\big(H_y-(\cal{H_{\cal{D}}}{\bf{w^{\it{init}}}})_y\big)}{\partial{x}}-\frac{\partial\big(H_x-({\cal{H_{\cal{D}}}{\bf{w}}^{\it{init}}})_x\big)}{\partial{y}}\Big]\end{cases}$$
After the incident electric fields are determined, the contrast function, which represents the EPs, can be calculated using $$${\cal{X}}=\frac{{\bf{w}}^F(E^{\it{inc}}+{{\cal{L}}_{\cal{D}}{\bf{w}}^F})}{|E^{\it{inc}}+{\cal{L}}_{\cal{D}}{\bf{w}}^F|^2}$$$, where $$${\cal {L_{\cal{D}}}}$$$ is an operator 5 and $$${\bf{w}}^{\it{F}}$$$ is the reconstructed contrast source after $$$H_z$$$ component was taken into account.
The convergence rate of the proposed method is compared with two traditional contrast source initialization methods expressed as $$${\bf{w}}^{\it{init}}=0$$$ (denoted as Method A) and $$${\bf{w}}^{\it{init}}=\frac{||{g^2}||}{||{\cal{K_{\cal{D}}g}||^2}}$$$ (denoted as Method B, and $$${\cal{K}}_{\cal{D}}$$$ and $$$g$$$ are relevant operator and variable 5). To calculate the electromagnetic fields used in this simulation based study, the finite-difference time-domain based electromagnetic simulation was assisted by Sim4Life by ZMT (https://www.zurichmedtech.com/sim4life/) with eight dipole coils driven at 300 MHz. The dipoles were evenly distributed on the transverse plane with an ellipse contour which has semi-major axe of 150 mm and semi-minor axe of 120 mm. The Duke model 6 with voxel size of $$$2mm\times2mm\times2mm$$$ was used in the simulation.
Results
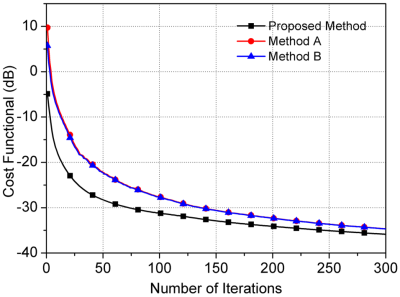
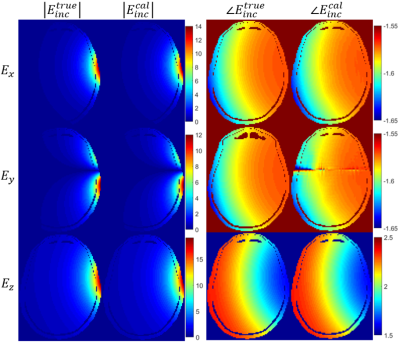
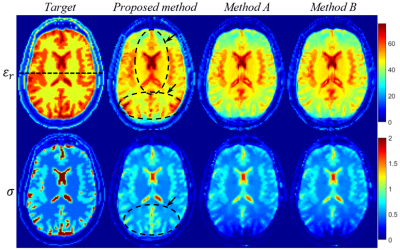
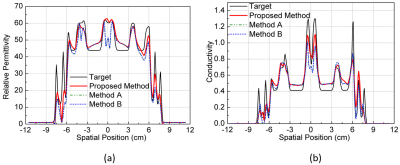
The convergence rates of all methods are shown in Figure 1 for comparison and it can be observed that the proposed method converged much faster than the traditional methods. The proposed method achieved close to -30 dB convergence after 60 iterations, whereas the traditional methods required 130 iterations for the same level of convergence. The calculated and true incident electric fields along three directions for the 1st dipole were shown in Figure 2 (the 50th axial slice was selected). It can be seen that both the magnitude and phase of the electric fields can be calculated accurately. The influences of different contrast source initialization methods on the EPs reconstruction were shown in Figure 3-4, when 300 iterations were allowed with all initialization. It can be seen that compared with methods A and B, the proposed method achieved more accurate EPs reconstruction especially for the gray matter and cerebrospinal fluid.Conclusion and Discussion
The initialization of contrast source from differential form of Maxwell’s equations dramatically improves the convergence rate of integral-based MR-EPT methods. It also provides the possibility to calculate the incident electric fields, which are essential in integral-based methods.Acknowledgements
No acknowledgement found.References
1. Schmidt R, Webb A. A new approach for electrical properties estimation using a global integral equation and improvements using high permittivity materials. J. Magn. Reson, 2016, 262: 8-14.
2. Balidemaj E, van den Berg C A T, Trinks J, et al. CSI-EPT: a contrast source inversion approach for improved MRI-based electric properties tomography. IEEE Trans. Med. Imag, 2015, 34(9): 1788-1796.
3. Hong R, Li S, Zhang J, et al. 3-D MRI-Based Electrical Properties Tomography Using the Volume Integral Equation Method. IEEE Trans. Microw. Theory and Tech, 2017.
4. Liu J, Zhang X, Schmitter S, et al. Gradient‐based electrical properties tomography (gEPT): A robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging. Magn Reson Med, 2015, 74(3): 634-646.
5. Guo L, Jin J, Liu C, Liu F, Crozier S. An Efficient Integral-based Method for Three-dimensional MR-EPT and the Calculation of the RF-Coil Induced Field. IEEE Trans. Biomedical. Eng. 2017 Oct 16.
6. Christ A, Kainz W, Hahn E G, et al. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Biol, 2009, 55(2): N23.
Figures