5614

Dual Echo Water-Fat Separation Using Deep Learning

Tao Zhang¹, Yuxin Chen², Shreyas Vasanawala³, and Ersin Bayram¹

¹Global MR Applications and Workflow, GE Healthcare, Houston, TX, United States, ²Electrical Engineering, Princeton University, Princeton, NJ, United States, ³Radiology, Stanford University, Stanford, CA, United States

Synopsis

Water-fat separation is widely used in many MR applications and is known to be challenging in various situations. Traditionally, region growing, spatial smoothing, and global optimization have been applied in dual echo water-fat separation. These methods require complex-valued images acquired at two echo times and occasionally suffer from global or local swaps due to inaccurate field map estimation. In this work, a deep learning approach for dual echo water-fat separation is investigated.

Introduction

Water-fat separation is widely used in many MR applications and is known to be challenging in various situations. Traditionally, region growing, spatial smoothing, and global optimization have been applied in dual echo water-fat separation [1-5]. These methods require complex-valued images acquired at two echo times and occasionally suffer from global or local swaps due to inaccurate field map estimation. In this work, a deep learning approach for dual echo water-fat separation is investigated. Water-only images are directly generated from magnitude images at two echo times through a U-Net [6] deep neural network.

Methods

Dual echo Dixon imaging can be modeled as:

$$$S_1=(W+c_1F)e^{i\phi_1},\\S_2=(W+c_2F)e^{i\phi_2},$$$ (1)

where $$$S_1$$$ and $$$S_2$$$ are pixel-wise complex composite signals acquired at two echo times, $$$W$$$ and $$$F$$$ are real-valued water and fat signal at each image pixel, $$$c_1$$$ and $$$c_2$$$ are dephasing factors for fat with respect to water corresponding to the two echo times, and $$$\phi_1$$$ and $$$\phi_2$$$ are additional phases attributed to field inhomogeneity. There are more unknowns ($$$W$$$, $$$F$$$ and $$$\phi_1$$$/$$$\phi_2$$$) than the number of linear equations, therefore Eq. (1) has multiple solutions. Traditional methods rely on the fact that the underlying field map is smooth to down-select the optimal solution. However, this process can be challenging, and, for certain optimization methods, time-consuming [4-5]. Note that the final solutions for water and fat can be written as functions of $$$S_1$$$ and $$$S_2$$$, although these functions cannot be easily approximated.

$$$W=f_1(S_1,S_2),\\F=f_2(S_1,S_2),$$$ (2)

In this work, we employ a deep neural network to approximate Eq. (2). Furthermore, since neural network can effectively estimate nonlinear functions, we approximate a mapping on magnitude images instead of complex-valued images. For simplicity, we only focus on estimating $$$W=f(|S_1|,|S_2|)$$$ for the rest of this work.

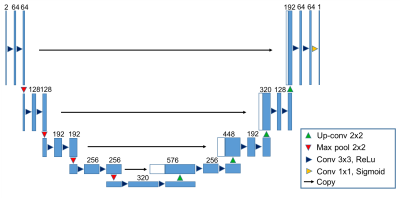
Deep Learning: we applied a modified U-Net neural network (Fig. 1) in this work. U-Net is a popular architecture for image segmentation, in which image pixels are labelled to different tissue types and the functions to be approximated are therefore discrete [6]. In comparison, the water-fat separation problem requires the neural network to approximate a continuous function $$$W=f(|S_1|,|S_2|)$$$. Thus, the loss function for U-Net needs to be carefully chosen. Here, a structural dissimilarity (DSSIM) metric is applied as the loss function [7]. Compared to traditional $$$\ell_2$$$ or $$$\ell_1$$$ loss functions, DSSIM better represents the human perception of images.

Data Preparation: With IRB approval and patient consent, 24 patients were recruited for dual echo Dixon imaging on MR750 3T scanners (GE Healthcare, Waukesha, USA). The imaging parameters were: TE1/TE2 = 2.2/3.3 ms, TR = 6.3-7.3 ms, and bandwidth = $$$\pm$$$ 100kHz. Global optimization [5] was used to obtain water-only images. Two board-certified radiologists reviewed and confirmed no obvious global or local water-fat swaps existed in these water-only images. A total of 9048 2D images from 20 patients were used to train the neural network, with 20% of the images for cross-validation. Another 1696 images from the remaining 4 patients were used for testing. All images were normalized and scaled to a fixed size of 256x256 during preprocessing.

Implementation: The proposed method was implemented in Python using Keras [8] and Tensorflow [9]. U-Net was trained with stochastic gradient descent (learning rate = 0.1, decaying factor = 5e-5, batch size = 16, and Nesterov momentum = 0.9). Training and testing were performed on a standard desktop with a GTX 1080 Nvidia GPU (Nvidia, Santa Clara, USA).

Results

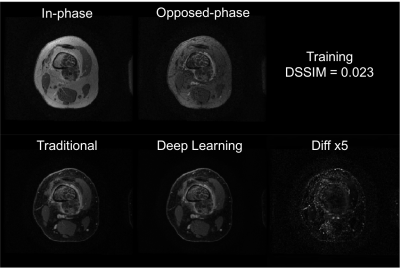
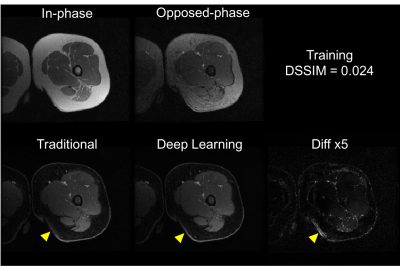
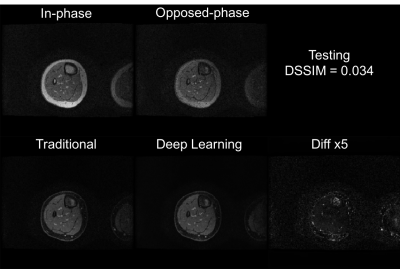
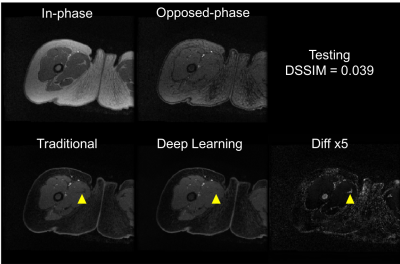
Training of the proposed neural network converged with DSSIM losses for both training and cross-validation at 0.023. The averaged loss for the test set was 0.031. With a pre-trained U-Net, it took only approximately 10 ms to generate a water-only image for one set of 2D images (256x256), significantly faster than traditional methods. Representative images are shown in Fig. 2 and Fig. 3 for the training set, and Fig. 4 and Fig. 5 for the test set. Overall, similar image quality between the traditional method and the proposed method was observed. The proposed method can occasionally correct minor inaccuracy from the traditional method (Fig. 3), but can also occasionally suffer from noticeable inaccuracy (Fig. 5).

Discussion

In this work, we have demonstrated the feasibility of applying deep learning to dual echo water-fat separation. Compared to previous work, in which deep learning was used to estimate the field map for multi-echo Dixon imaging [10], the proposed method can achieve water-fat separation from magnitude-only images, thus simplifying the workflow. Future works will focus on the improvement of accuracy for the proposed method and the extension to other MR applications.

Acknowledgements

We acknowledge the support of NIH R01 EB009690.

References

[1] Ma J. Breath-hold water and fat imaging using a dual-echo two-point Dixon technique with an efficient and robust phase-correction algorithm. Magn Reson Med 2004;52:415-419

[2] Xiang Q. Two-point water-fat imaging with partially-opposed-phase (POP) acquisition: an asymmetric Dixon method. Magn Reson Med 2006;56:572-584

[3] Eggers H, Brendel B, Duijndam A, Herigault G. Dual-echo Dixon imaging with flexible choice of echo times. Magn Reson Med 2011;65:96-107

[4] Berglund J, Ahlstrom H, Johansson L, Kullberg J. Two-point Dixon method with flexible echo times. Magn Reson Med 2011;65:994-1004

[5] Zhang T, Chen Y, Bao S, et al. Resolving phase ambiguity in dual-echo Dixon imaging using a projected power method. Magn Reson Med 2017;77:2066-2076

[6] Ronneberger O, Fischer P, Brox T. U-Net: Convoluntional Networks for Biomedical Image Segmentation. arXiv preprint arXiv:1505.04597, 2015

[7] Wang Z, Bovik, A, Sheikh, H, Simoncelli, E. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004;13:600-612

[8] Chollet F, et al. Keras, 2015. https://github.com/fchollet/keras

[9] Abadi M, et al. TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. https://www.tensorflow.org

[10] Gong E, Zaharchuk G, Pauly J. Improved Multi-echo Water-fat Separation Using Deep Learning. ISMRM 2017. p5657

Figures

Fig. 1 U-Net neural network for dual echo water-fat separation. Major components of the network are illustrated by different symbols, including up convolution, max pooling, and convolution with different kernel sizes and activation functions. The number of feature maps (also known as the depth of each layer) is shown on top of each layer. The network takes two 2D images as inputs and generates the corresponding water-only image as the output.

Fig. 2 Representative images from the training set. Similar image quality is achieved using deep learning compared to the traditional method.

Fig. 3 Representative images from the training set. Similar image quality is achieved using deep learning compared to the traditional method. Note that deep learning was able to correct minor water-fat separation inaccuracy from the traditional method (arrowhead).

Fig. 4 Representative images from the test set. Similar image quality is achieved using deep learning compared to the traditional method.

Fig. 5 Representative images from the test set. Similar image quality is achieved using deep learning compared to the traditional method. Minor water-fat separation inaccuracy was noticed in the deep learning result (arrowhead).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5614