5611
A non-local low rank approach for high resolution parameter mapping1Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 2Department of Medical Imaging, University of Arizona, Tucson, AZ, United States
Synopsis
Inversion recovery (IR) based single-shot approaches have become popular for rapid T1 mapping. Due to the highly accelerated nature of the acquisition, it is challenging to generate high quality contrast images and T1 maps from this dataset. To tackle this problem, we present a non-local low rank regularization model that is inspired by block matching approaches. For a given relaxation signal, we identify the top L similar relaxation signals within a spatial neighborhood and constrain them to have a low rank. We demonstrate this approach in single-shot high-resolution radial steady-state-free-precession (SSFP) brain and abdomen imaging.
Introduction
Sequences like the IR-SSFP are capable of yielding a train of contrast weighted images at different inversion times (TI) following a single IR pulse making them single-shot approaches for T1 mapping1-3. Several models based on leveraging the high degree of redundancy in TI images can be used to handle the problem of image reconstruction from this highly under-sampled dataset1-7. One popular approach involves promoting low rank and locally low-rank (LLR) behavior across the contrast images via a surrogate for rank such as the nuclear norm4. A stronger form of the rank constraint can be enforced via subspace-constrained reconstruction models3,5-7. While yielding high quality images at most TI points, the subspace constraint yields poor images in the early TIs which can significantly affect the underlying T1 estimates. In this work, we propose a reconstruction model inspired by block matching and LLR regularization to create TI images that yield significantly improved T1 maps.Reconstruction models
Consider a data model, $$$\mathbf{Y}=\mathbf{E(X)}$$$, where $$$\mathbf{Y}$$$ is the measured k-space data, $$$\mathbf{X}$$$ is the set of contrast-weighted images, and $$$\mathbf{E}$$$ is the combined Fourier-sensitivity encoding operator. For subspace-constrained reconstructions, a subspace basis, $$$\mathbf{\Phi}^{'}_{K}$$$, maps the $$$N$$$ contrast images into a $$$K$$$ $$$(<<N)$$$ dimensional subspace6,7. The subspace-constrained reconstruction3 is posed as:
$$\min_\alpha||\mathbf{Y}-\mathbf{E(\Phi}_{K}\alpha)||_2^2+\lambda TV(\mathbf{\alpha})$$
where $$$\mathbf{\alpha}$$$ are subspace basis images $$$(\mathbf{\alpha}=\mathbf{\Phi}^{'}_{K}\mathbf{X})$$$ which this reconstruction method seeks to recover. $$$TV(.)$$$ is a total variation regularization and $$$\lambda$$$ governs the strength of regularization. The basis, $$$\mathbf{\Phi}^{'}_{K}$$$, can be estimated from a suitable signal model via SVD3,6. The reconstructed images, $$$\mathbf{X}$$$, are fit to the signal model to extract the T1 map.
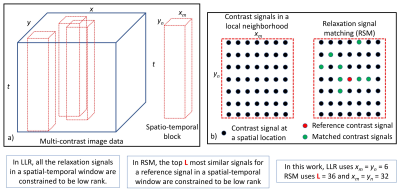
Constrained reconstruction of the TI frames using an LLR regularization4 can be cast as:
$$\min_\mathbf{X}||\mathbf{Y}-\mathbf{E(X)}||_2^2+\lambda \sum_j||R_j(\mathbf{X})||_*$$
where the operator $$$R_j(.)$$$ extracts the relaxation signals about a small spatial window centered on the $$$j^{th}$$$ spatial pixel and enforces low rank penalties via the nuclear norm. This penalty promotes low rank behavior across the relaxation signals in a small spatial window and the window is tiled across the imaging scene.
The model proposed in this work, relaxation signal matching (RSM), takes a form similar to the LLR reconstruction but we modify the operator $$$R_j(.)$$$ as follows: For the relaxation signal in the $$$j^{th}$$$ spatial pixel, the operator $$$R_j(.)$$$ extracts the L most similar signals (in $$$\ell_2$$$ sense) and orders them into a matrix. Due to the signal matching step, this approach can extract signals further away from the immediate neighborhood of pixel $$$j$$$. This makes it a non-local rank approach and enhances the low-rank nature of the matrix being constrained. An illustration of both these models is provided in Figure 1. The LLR and RSM models as discussed above operate on the contrast dimensional space, but we note that it is trivial to add a subspace constraint as a post reconstruction filter as follows: $$$\mathbf{X_{filtered}}=\mathbf{\Phi}_{K}\mathbf{\Phi}^{'}_{K}\mathbf{X}$$$. This serves to substantially enhance the quality of the TI images without affecting the quality of the T1 maps.
Methods and Results
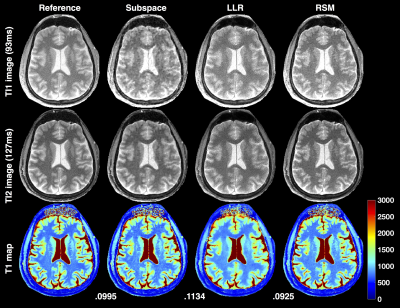
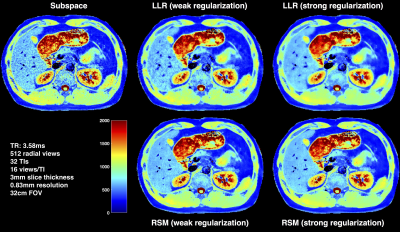
The radial IR-SSFP sequence was implemented on a 3T Siemens Skyra scanner with tiny golden angle radial view ordering8. We use normalized mean squared error (NMSE) in the brain dataset (where a fully sampled reference can be acquired) to quantify performance. Representative results from abdomen imaging are also presented. Figure 2 shows the results on the brain dataset. Figure 3 shows the sample T1 maps created from the different models on the abdomen dataset where results at two different regularization levels are shown for LLR and RSM.
Figure 4 shows sample TI frames from the different models along with the associated T1 maps demonstrating the benefits of the post reconstruction filter. RSM reconstructions while being sharp exhibit remnants of artifact that are present in all the TIs (note that the artifact varies spatially across TIs). The subspace filter is built from the signal model and this spatially varying artifact is effectively removed with the RSM+filter reconstruction.
Discussion and Conclusion
We have developed a new reconstruction model that enforces a spatially non-local low rank constraint on contrast signals in the imaging scene and generates parameter maps with good preservation of high frequency content. A model-subspace based projection filter is used to further reduce residual artifacts across the TI images yielding contrast-weighted images suitable for diagnostic analysis. Our results on high resolution brain and abdomen T1 mapping demonstrate that the proposed approach yields high quality parameter maps.Acknowledgements
The authors would like to acknowledge support from the Arizona Biomedical Research Commission (Grant ADHS14-082996) and the Technology and Research Initiative Fund (TRIF) Improving Health Initiative.References
1. Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahms J. Model based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. MRM, 2017; doi:10.1002/mrm.26726
2. Tran-Gia J, Wech T,Bley T, Kostler H. Model based acceleration of Look-Locker T1 Mapping. Plos One, 2015, 10.
3. Li Z, Berman BP, Galons JP, Bilgin A, Altbach MI, Martin DR. Rapid high-resolution T1 mapping using highly accelerated radial steady-state free-precession acquisition. ISMRM, Singapore, 2016. p. 4196.
4. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. MRM, 2014;73:655-661.
5. Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis. MRM, 2011;66:706–716.
6. Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. MRM, 2012;67:1355–1366.
7. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low‐rank and sparsity constraints. MRM, 2015;74: 489-498.
8. Wundrak S, Paul J, Ulrici J, Hell E, Rasche V. A small surrogate for the golden angle in time resolved radial MRI based on generalized Fibonacci sequences. IEEE Trans Med Imaging 2014;34:1262–1269.
Figures