INTRODUCTION

The interest in viscoelastic parameters obtained from MR Elastography has grown continuously since the development of the method, and preliminary results have indicated the potential of these damping properties as biomarkers for a number of targets, including the liver and the brain¹. Viscous property characterization has now begun to seek to identify the parameters describing the spectral tissue response across a range of frequencies through power-law (PL) models that can be related to multi-scale effects in both scattering² and fluid-solid interactions³. This work presents the development of a multi-frequency reconstruction method based on a power-law model (PL-MF MRE) for the storage and loss modulus. The PL-MF MRE reconstruction method is presented via in-vivo data in the human brain and the resulting PL parameters are compared to values obtained from regression of mon-frequency reconstructions.

METHODS

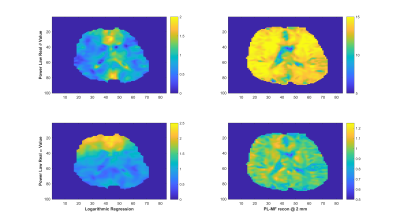
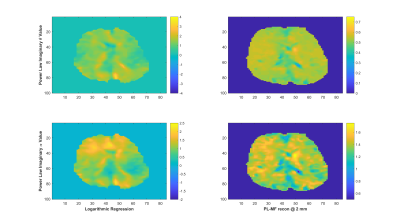
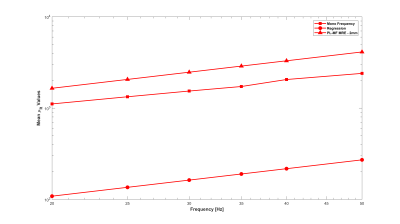
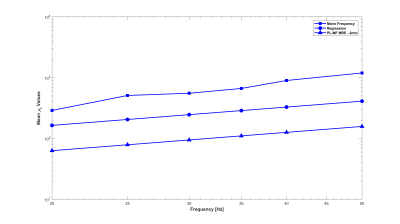
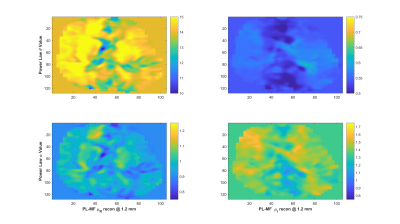
Experiments were conducted on a 1.5-T Siemens MAGNETOM Sonata using single-shot spin-echo EPI with trapezoidal flow-compensated MEGs in all three directions⁴. The actuator employed was similar to the head rocker system described by Sack et al⁵., with the setup detailed by Guo et al⁶. Full 3D displacement fields at 15, 20, 25, 30, 35, 40 and 50 Hz were obtained in healthy volunteers. Guideline Values: Guidelines for the PL parameters for the viscoelastic material properties were established via mono-frequency reconstructions using non-linear inversion (NLI)⁷. The resulting distributions for μ_R and μ_I were fit to independent PL models, μ_R = θ_R·ω^α_R and μ_I = θ_I·ω^α_I, through a logarithmic regression at each voxel⁸, providing distributions and volumetric means of θ_R, α_R, θ_I and α_I, as well as the RMS error for the regression fit. PL-MF MRE: The same displacement fields were then provided to a NLI based PL-MF MRE reconstruction algorithm, based on finite element methods and adjoint-gradient based optimization⁹ of the objective function, $$\Phi=\frac{1}{2}\sum_{i=1}^{N_{freq}}\|u_c(\omega_i)-u_m^i\|.^2$$ Total Variation (TV) regularization was applied to counteract decreased stability of the inversion given the strict application of the PL model. The results from the PL-MF MRE reconstruction are the real and imaginary shear modulus PL parameters, θ_R, α_R, θ_I and α_I, for the frequency range provided. The distributions and volumetric averages of these parameters were compared with the guideline values obtained by logarithmic regression. Super-resolution MRE: While MRE is technically ‘super-resolution’ by default, due to the shear wavelength being longer than typical imaging voxel resolutions, it is possible to reconstruct material properties at resolutions finer than the imaging resolution, provided sufficient data¹⁰. Here, the presence of 6 measurements (real and imaginary displacements in 3 directions) at each frequency, versus the 4 parameters to be reconstructed, (θ_R, α_R, θ_I, α_I), permitted reconstruction at finer resolution than the measured displacement data. For the finite element implementation used for the PL-MF MRE reconstruction, the limiting factor for the reconstruction resolution was the resolution of the Gauss points used to integrate the state equations for the calculated displacements. For the 2 mm isotropic voxels used here, material parameter resolutions smaller than 1.2 mm would generate cases where the resulting material property had no influence on the displacement values, thus limiting reconstruction resolution unless the measured displacements were interpolated onto a finer resolution mesh, which was not done in this case. Super-resolution distributions of θ_R, α_R, θ_I and α_I were calculated on 1.2 mm voxels using the same PL-MF MRE method used for 2 mm voxels.

RESULTS

As reported in Testu et al⁸., mono-frequency reconstructed properties were generally well described by a power-law model, except in the region of the falx cerebri. The TV stabilized PL-MF MRE reconstruction provided similar PL parameters to the regression results, with image definition clearly improved through the incorporation of multiple displacement fields into the NLI algorithm. Figures 1 and 2 compare the guideline values for the PL parameters and those from the PL-MF MRE reconstruction for the real and imaginary shear modulus, respectively. Figures 3 and 4 show the resulting fit to the mono-frequency real and imaginary shear modulus values, respectively. Finally, Figure 5 shows the super-resolution PL parameters at 1.2 mm, reconstructed via PL-MF MRE. In general, guideline PL parameter values are in good agreement with those obtained by PL-MF MRE, with the largest disagreements coming in regions of high RMS error for the logarithmic regression.

CONCLUSIONS

This preliminary demonstration of a PL-MF MRE method able to match the PL parameters obtained from regression analysis of mono-frequency reconstruction results provides an important step toward accurate and verifiable quantification of the dispersive, multi-scale nature of soft-tissue.

Acknowledgements

This work was supported in part by NIH Grants R01-EB018230 awarded by the National Institute of Biomedical Imaging Bioengineering and R01-AA023684 awarded by the National Institute on Alcohol Abuse and Alcoholism. Financial support of the Bundesministerium fr Bildung und Forschung (BMBF 01GQ1408) is gratefully acknowledged. EEWVH acknowledges financial support from NSERC (Discovery Grant #435399-2013) for this work and is a member of the FRQ-S-funded Centre de recherche du Centre hospitalier universitaire de Sherbrooke (CR-CHUS).