5597

Wave propagation in multi-excitation magnetic resonance elastography of the brain

Daniel R Smith¹, Philip V Bayly², Anthony J Romano³, and Curtis L Johnson¹

¹Biomedical Engineering, University of Delaware, Newark, DE, United States, ²Mechanical Engineering and Materials Science, Washington University in St. Louis, St. Louis, MO, United States, ³Naval Research Laboratory, Code 7160, Washington, DC, United States

Synopsis

MR elastography (MRE) is capable of measuring the mechanical properties of the human brain; however, MRE generally assumes isotropic properties and misses the anisotropic behavior of brain white matter. Anisotropic MRE methods are under development, and the use of multiple wave propagation directions is likely necessary for accurate inversion. In this work, we characterize waves in brain MRE from multiple excitations and evaluate whether sufficient wave propagation is present. We find that multi-excitation MRE motion fields in the brain exhibit wave content in white matter tracts sufficient for anisotropic inversion.

Introduction

Magnetic resonance elastography (MRE) can quantify the viscoelastic stiffness of brain tissue¹; however, most MRE methods consider the tissue as isotropic, while the ordered nature of axon fibers causes brain white matter (WM) to exhibit mechanical anisotropy². Efforts to use anisotropic MRE are ongoing, although multiple wave propagation directions are likely necessary^3-6. Accurate characterization of transversely isotropic materials requires consideration of both slow and fast components of propagating waves^7-9. Tweten et al recently described three key wave propagation criteria for accurate anisotropic inversion⁸: presence of multiple slow and fast shear waves, with propagation directions at least 15° apart, each with filtered wave amplitudes above a threshold of at least 20% of the total amplitude. Multiple plane waves generally exist at most points in the brain during MRE, due to the source-like behavior of multiple contact points between the skull and the brain, even from a single excitation^10,11, however, it is not clear that this is sufficient for accurate estimation. Multi-excitation MRE¹² can also be used to generate waves with different propagation directions to meet the minimum criteria. The purpose of this work is to characterize wave propagation from multiple excitations and evaluate whether criteria for anisotropic MRE are satisfied in WM tracts.

Methods

Subjects: We studied four healthy subjects (3/1 M/F; 22-32 years old) using a Siemens 3T Prisma scanner with 20-channel head coil.

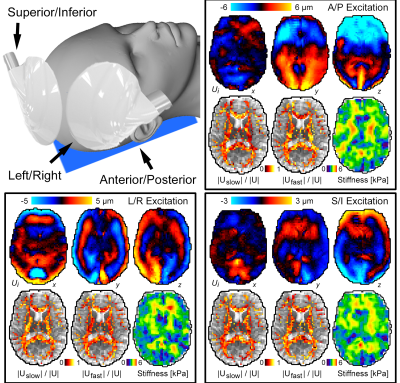
Imaging: Three separate MRE scans were acquired at 50 Hz, one for each of three excitation directions: anterior-posterior (AP), left-right (LR), and superior-inferior (SI). Excitations were generated by an active pneumatic driver (Resoundant) with three passive drivers (Figure 2a): a pillow-driver for AP excitation, and pads placed lateral and superior for LR and SI excitations. MRE scans used an EPI sequence with 3 x 3 x 3 mm³ isometric voxels with a total FOV of 240 x 240 x 144 mm³. Auxiliary scans included diffusion tensor imaging (DTI) with resolution and FOV matched to MRE to estimate fiber direction, and T1-weighted MPRAGE at 0.9 mm resolution to localize tracts.

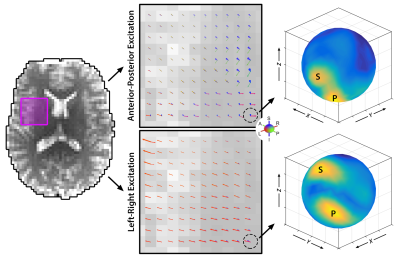
Analysis: From each MRE displacement field, we estimated wave propagation directions using directional filtering^7,13 using 300 directions distributed over the unit sphere. At each voxel, we determined primary and secondary wave propagation directions and amplitudes (Figure 1). After isolating waves propagating in each direction,$$$\overrightarrow{N}$$$; we determined the polarization of the slow and fast components ($$$\overrightarrow{m_{s}}$$$ and $$$\overrightarrow{m_{f}}$$$) by comparing with fiber direction from DTI,$$$\overrightarrow{A}$$$: $$$\overrightarrow{m_{s}}=\overrightarrow{N}\times\overrightarrow{A}$$$; $$$\overrightarrow{m_{f}}=\overrightarrow{N}\times\overrightarrow{m_{s}}$$$. We projected the directionally-filtered motion field on these polarization directions, and classified as slow and/or fast if this amplitude is at least 20% of the total amplitude⁸. The number of voxels which fit the necessary criteria for anisotropic MRE were estimated as a percentage of overall WM (determined from DTI by fractional anisotropy threshold of 0.25), as of individual tracts (corpus callosum (CC), corona radiata (CR), corticospinal tract (CST), and superior longitudinal fasciculus (SLF), registered from an atlas using FSL^14,15).

Results

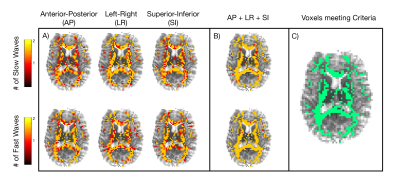
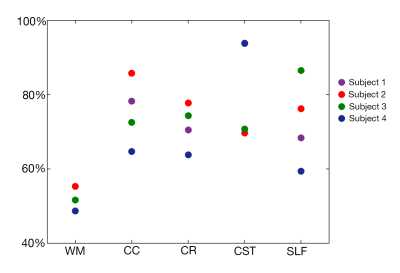
Figure 1 shows the primary and secondary propagation directions at selected voxels, from two different excitations. Figure 2 presents full vector displacement fields for each excitation in one subject, along with the relative contributions of slow and fast shear waves. The relative slow/fast contributions differ in white matter tracts for different actuations; this may account for differences in the apparent isotropic stiffness maps. We quantified the number of slow or fast waves that meet the amplitude threshold (20%); Figure 3 shows maps of the results for each excitation and all three excitations combined (excluding redundant directions), as well as the set of WM voxels that (using multiple excitation) satisfy the three major criteria for anisotropic inversion. Figure 4 shows the percentage of voxels that fit these criteria in each subject. On average, 51.8% of the voxels in WM met the criteria; this number is higher in individual tracts (CC = 75.3%; CR = 71.6%; CST = 82.0%; SLF = 72.6%).

Discussion and Conclusions

By directional filtering of MRE displacement fields in the brain, we can identify multiple shear waves with different propagation directions at most voxels, and verify that both slow and fast shear waves are present in most cases. Using multiple excitations, we generate different propagation directions and increase the number of voxels that meet minimum criteria for anisotropic inversion, especially in major tracts. These findings suggest that in future studies, by using multiple excitations and spatial filtering to decompose the wave motion into dominant propagation directions, sufficient information should be available to characterize the anisotropic properties of brain WM.

Acknowledgements

This was supported by the Office of Naval Research (N00014-17-P-7001) and the Delaware INBRE Program through NIH/NIGMS (P20-GM103446).

References

1) Hiscox, L. V, et al. (2016). Magnetic resonance elastography (MRE) of the human brain: technique, findings and clinical applications. Physics in Medicine and Biology, 61(24), R401–R437.

2) Feng, Y., et al. (2013). Viscoelastic properties of the ferret brain measured in vivo at multiple frequencies by magnetic resonance elastography. Journal of Biomechanics, 46(5), 863–870.

3) Green, M. A., et al. (2013). Measuring anisotropic muscle stiffness properties using elastography. NMR in Biomedicine, 26(11), 1387–1394.

4) Guo, J., et al. (2016). Three-parameter shear wave inversion in MR elastography of incompressible transverse isotropic media: Application to in vivo lower leg muscles. Magnetic Resonance in Medicine, 75(4), 1537–1545.

5) Sinkus, R., et al. (2005), Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography. Magn. Reson. Med., 53: 372–387.

6) Romano, A., et al. (2014). In vivo waveguide elastography: Effects of neurodegeneration in patients with amyotrophic lateral sclerosis. Magnetic Resonance in Medicine, 72(6), 1755–1761.

7) Tweten, D. J., et al. (2015). Estimation of material parameters from slow and fast shear waves in an incompressible, transversely isotropic material. Journal of Biomechanics, 48(15), 4002–4009.

8) Tweten, D. J., et al. (2017). Requirements for accurate estimation of anisotropic material parameters by magnetic resonance elastography: A computational study. Magnetic Resonance in Medicine.

9) Schmidt, J. L., et al. (2016). Magnetic resonance elastography of slow and fast shear waves illuminates differences in shear and tensile moduli in anisotropic tissue. Journal of Biomechanics, 49(7), 1042–1049.

10) Romano, A., et al. (2012). In vivo waveguide elastography of white matter tracts in the human brain. Magnetic Resonance in Medicine, 68(5), 1410–1422.

11) Clayton, E. H., et al. (2012). Transmission, attenuation and reflection of shear waves in the human brain. Journal of the Royal Society, Interface, 9(76), 2899–910.

12) Anderson, A. T., et al. (2016). Observation of direction-dependent mechanical properties in the human brain with multi-excitation MR elastography. Journal of the Mechanical Behavior of Bomedical Materials, 59(6), 538-546.

13) Manduca, A., et al. (2003). Spatio-temporal directional filtering for improved inversion of MR elastography images. Medical Image Analysis, 7(4), 465–473.

14) Mori, S., et al. (2008). Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. NeuroImage, 40(2), 570–582.

15) Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W., & Smith, S. M. (2012, August 15). FSL. NeuroImage. Academic Press.

Figures

Figure 1: Comparison of primary and secondary wave propagation directions from AP & LR excitations (middle). Propagation directions were found by directional-filtering in 300 directions and plotting filtered amplitude on a sphere (right); the primary (P) direction is the direction with maximum amplitude, the secondary (S) direction is the distinct direction with the next-highest amplitude

Figure 2: Experimental setup with positioning of passive drivers for multi-excitation MRE (top left). Analysis results for three MRE excitations: AP (top right), LR (bottom left), and SI (bottom right): The individual displacement fields from MRE (top row); relative contributions of slow and fast shear waves (left and center of bottom row); and estimated isotropic stiffness maps (bottom right);

Figure 3: A) The number of slow or fast shear waves (max two each) that contribute at least 20% of total displacement amplitude, for each excitation, in each WM voxel. B) The combined number of slow or fast waves from all three excitations, excluding redundant directions, that meet the 20% threshold. C) Map of voxels that meet the criteria of having at least two slow waves and two fast waves with amplitude > 20% of total, from all excitations.

Figure 4: The percentage of voxels per tract that fit the three major criteria for characterizing anisotropy (slow and fast shear waves; at least two distinct directions; at least 20% amplitude) using all three excitation directions (AP, LR, and SI).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5597