Synopsis

Poroelastic and viscoelastic inversions in a 1Hz experimental MR Elastography phantom system were investigated theoretically, numerically, and experimentally. At low frequencies, viscoelastic models have a non-uniqueness issue that can be avoided by using a poroelastic model, which has an additional fluid force term to balance elastic forces when inertial forces are negligible. Numerical experiments showed poroelastic models have much higher sensitivity to global property changes compared to viscoelastic models. Inversions of experimental phantom data with a poroelastic model gave cleaner images that are less sensitive to initial property estimates compared to a viscoelastic model.

Introduction

MR elastography produces quantitative images of tissue mechanical properties, which are correlated with a wide variety of diseases. As these mechanical properties cannot be imaged directly, deformation must be induced in the tissue to solicit information on the tissue mechanical structure and provide a measurable displacement field. Typically, 30-100Hz external vibration is used, which produces a steady state mechanical wave field. Recently, intrinsic actuation has been applied to brain tissue, which uses the natural pulsation of blood and CSF during the cardiac cycle as the source of deformation and does not require an external vibration source¹. Intrinsic motion is at much lower frequencies (~1Hz) compared to external actuation, and this quasi-static deformation state creates new issues for property recovery inverse problems. The wavelength of 1Hz shear waves are on the order of 1-3m, which causes problems for local frequency estimation and other direct inversion algorithms. Nonlinear inversion is a model based strategy which iteratively updates a spatially discretized estimate of mechanical properties in a finite element model so that the difference between the measured and model displacements are minimized, and can work for a wide range of frequencies. Both viscoelastic² and poroelastic³ models have been applied, and it has been demonstrated through simulated data that correct model choice is important at lower actuation frequencies⁴.

The viscoelastic governing equations for the displacement field, $$$u$$$, are

$$\triangledown\cdot\mu\left(\triangledown u+\triangledown u^T\right)+\triangledown \frac{2\mu \nu}{1-2\nu}\triangledown u=-\rho \omega^2 u$$

where the elastic properties are the shear modulus, $$$\mu$$$, poisson ratio, $$$\nu$$$, and density $$$\rho$$$. As the frequency, $$$\omega$$$, approaches zero, the $$$\rho \omega^2 u$$$ term quickly vanishes, representing the negligible inertial forces in low frequency motion. Since all LHS terms involve the shear modulus, $$$\mu$$$, a scalar $$$\mu_0$$$ can be pulled out of the equation, giving $$\mu_0\left[\triangledown\cdot\mu^*\left(\triangledown u+\triangledown u^T\right)+\triangledown \frac{2\mu^* \nu}{1-2\nu}\triangledown u \right] \approx 0.$$

Clearly, the scalar $$$\mu_0$$$ is arbitrary, and therefore leads to non-uniqueness at low frequencies where any scalar multiple of the property field, $$$\mu=\mu_0\mu^*$$$, can produce a given displacement field.

The poroelastic governing equations are

$$\triangledown\cdot\mu\left(\triangledown u+\triangledown u^T\right)+\triangledown \frac{2\mu \nu}{1-2\nu}\triangledown u +(1-\beta) \triangledown P=-\left( \rho-\phi\rho_f \right) \omega^2 u$$

$$\triangledown \cdot \beta \triangledown P+ \rho_f \omega^2 \triangledown \left( \left( 1-\beta \right) P \right)=0$$

Additional variables are the pressure field, $$$P$$$, fluid density $$$\rho_f$$$, porosity, $$$\phi$$$, and the term $$$\beta$$$, which is a function of hydrodynamic properties³. The form of $$$\beta$$$ does not allow arbitrary scaling with $$$\mu$$$, and $$$\beta$$$ cannot be 1, so the $$$(1-\beta) \triangledown P$$$ term avoids the non-uniqueness issue found in the viscoelastic equations at low frequency. This effect can be interpreted as the force of the fluid having an important contribution to the mechanical response, in addition to the elastic and inertial forces in the viscoelastic model. This work investigates the non-uniqueness issue for the two models using low frequency simulated and experimental phantom data.

Methods

Numerical experiments on a single 25mm cubic region (the size of an NLI subzone) compared the sensitivity of uniform changes in $$$\mu$$$ across the domain with changes in $$$\mu$$$ at a single internal node, for both models. Non-uniqueness with global changes in $$$\mu$$$ was investigated as a function of frequency for each model.

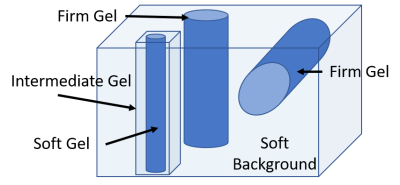
Gelatin phantoms with soft, intermediate and stiff components (3.5, 7 and 10.5%) were constructed (illustrated in figure 1) and hydraulically actuated at 1Hz using a computer-controlled electric pump pushing a shear plate. The resulting motions in 3D were imaged with the QFLOW sequence on a Philips Achieva 3T clinical scanner, and processed with viscoelastic and poroelastic reconstructions starting from different initial property estimates.

Results

The numerical experiments showed the expected singularity for the viscoelastic model; Figure 2 shows that at 1Hz, the sensitivity of the displacement field to a global parameter change was 3 orders of magnitude below that of changes at a single property node, whereas the poroelastic model maintained a much higher sensitivity to global property changes at all frequencies. Figure 3 shows the sensitivity of the displacement fields to changes in global and local $$$\mu$$$ values at 1Hz and 50Hz. The poroelastic model has high global sensitivity at both frequencies, whereas viscoelastic has very low global sensitivity at 1Hz due to non-uniqueness when inertial forces are small.

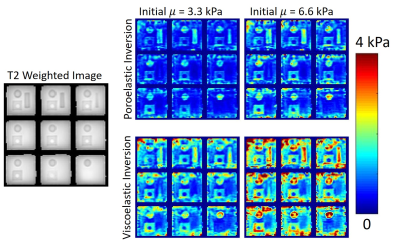
Inversion results in figure 4 show that although both models produce reasonable images, viscoelastic inversions appear noisier and more sensitive to the initial guess compared to poroelastic inversion. This may be due to issues with non-uniqueness at low frequency. Poroelastic inversion appears to be numerically more robust at lower frequencies, so it is particularly attractive for fluid-saturated media such as brain tissue.

Acknowledgements

References

[1] Weaver, John B., et al. "Brain mechanical property measurement using MRE with intrinsic activation." Physics in medicine and biology 57.22 (2012): 7275.

[2] McGarry, M. D. J., et al. "Multiresolution MR elastography using nonlinear inversion." Medical physics 39.10 (2012): 6388-6396.

[3] Perriñez, Phillip R., et al. "Contrast detection in fluid‐saturated media with magnetic resonance poroelastography." Medical physics 37.7 (2010): 3518-3526.

[4] McGarry, M. D. J., et al. "Suitability of poroelastic and viscoelastic mechanical models for high and low frequency MR elastography." Medical physics 42.2 (2015): 947-957.