5589
Experimental validation of appropriate conditions for accurate and precise Magnetic Resonance Elastography: an in vitro phantom study1Imagerie par Résonance Magnétique Médicale et Multi-Modalités, IR4M, CNRS, Univ Paris-Sud, Université Paris-Saclay, Orsay, France, 2Imagerie Moléculaire In Vivo, IMIV, Inserm, CEA, CNRS, Univ Paris-Sud, Université Paris-Saclay, Orsay, France
Synopsis
Magnetic Resonance Elastography (MRE) allows to non-invasively characterize the mechanical properties in vivo. The reconstruction performance is challenged by multiple experimental parameters, which can be grouped into two more comprehensive parameters: number of voxels per wavelength and acquired displacement field quality. In a previous in silico study, we have demonstrated that appropriate λ/a condition is crucial for accurate and precise MRE and proposed a quality parameter to effectively evaluate the voxel-wise reconstruction quality. This study experimentally validated these simulation findings on commercial model phantoms.
Introduction
Magnetic Resonance Elastography (MRE) is an emerging imaging modality, which allows to non-invasively characterize the mechanical properties in vivo. MRE exploits motion encoding gradient (MEG) to encode the displacement fields induced at the passage of propagating shear waves generated in the human body by external mechanical vibrations. The mechanical properties can then be deduced by inverting the Helmholtz equation governing the curl of the shear displacement field, q.1 The q-based reconstruction method may be flawless,2 however its performance is challenged by multiple experimental parameters. These parameters can be grouped into two more comprehensive parameters: number of voxels per wavelength (λ/a), where λ and a respectively represent the wavelength and voxel size, and q-field quality (|q|/Δ|q|), where |q| and Δ|q| respectively represent the q-field amplitude and its associated measurement uncertainty. In a previous in silico study, we have demonstrated that appropriate λ/a condition is crucial for accurate and precise MRE and |q|/Δ|q| is effective to evaluate the voxel-wise reconstruction quality.3 The aim of this study was to experimentally validate these simulation findings through an in vitro phantom study.Methods
Experimental protocol
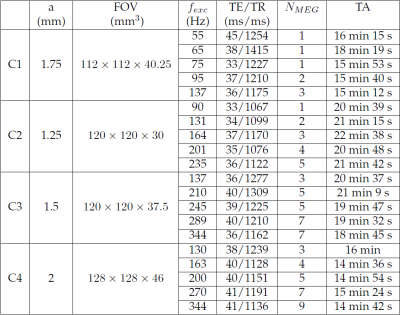
Four commercial model phantoms C1-C4 (Model 039, CIRS, Norfolk, VA, USA) were used for this study as they are isotropic,homogeneous and quasi-elastic media which correspond to the assumptions used in the simulation study. First, each phantom was characterized at five different excitation frequencies using the spin-echo based MRE sequence on a Philips 1.5 T MR Scanner (Achieva, Philips Healthcare, The Netherlands). The phantoms were placed horizontally into a commercial knee coil and a point source excitation was installed (Figure 1). MEG with amplitude 21mT/m was applied successively along the three spatial encoding directions. The number of MEG, NMEG, was adjusted according to the applied excitation frequency, fexc. Acquisition parameters are summarized in Figure 2. Second, each phantom was characterized by Transient Elastography (TE) on a FibroScan 502 TOUCH system (Echosens, Paris, France) using the probe M (3.5 MHz) at an excitation frequency of 50 Hz. The TE measurements serve as the reference values to evaluate the MRE measurement accuracy and precision.
Data analysis
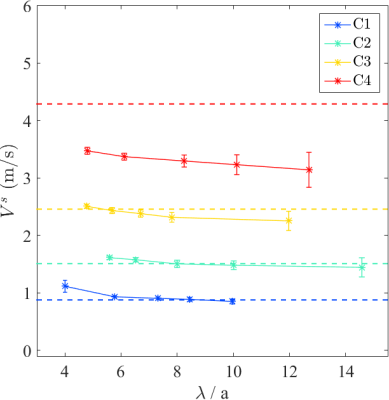
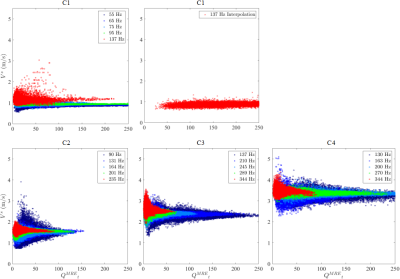
All the acquired MRE data sets were reconstructed using the q-based method.1 The q-based quality weighting strategy detailed in the previous simulation study was used to deduce the quality weighted shear velocity (Vs) maps accompanied with the associated |q|/Δ|q| maps.3 First, regions of interest (ROIs) with identical |q|/Δ|q| levels (40±4) and volumes as studied in the simulation were selected on all the obtained shear velocity maps. Mean values (MVs) and standard deviations (SDs) computed over these ROIs were evaluated as a function of λ/a. Second, for all the obtained Vs maps, Vs values were plotted against the corresponding |q|/Δ|q| values. For each phantom, ten valid TE measurements were acquired and the median of these values was taken as the final estimation.
Results
Figure 3 displays the Vs maps of all the calibrated phantoms for different excitation frequencies. MV±SD of Vs values over similar ROIs for all the phantoms were evaluated as a function of λ/a in Figure 4. Figure 5 presents the voxel-wise velocity-quality parameter clusters for all the reconstructed data sets.Discussion and Conclusion
Figure 3 and 4 show that the sensitivity of the overall MRE measurement is very high whatever the excitation frequency was used. However, the accuracy and precision of MRE measurements for each phantom depend on the excitation frequency, more exactly the λ/a ratio. Taking the TE measurements as reference values, it is obvious that the MRE measurement quality for phantoms C1-C2 first improves with λ/a, then worsens for larger λ/a ratios resulting in an appropriate λ/a range around 7-10, which corroborate well the simulation findings. The inconsistent observations for phantoms C3-C4 are mainly due to the coupling effect in the near field, which in fact leads to an overestimation for the TE measurements.4 For all the phantoms, the MRE measurements for different frequencies always converge to similar values when |q|/Δ|q| is high enough (Figure 5). Thus an empirically chosen quality parameter can be determined to guarantee the measurement validity. For some data sets at higher excitation frequencies, the shear velocity converges at slightly higher value as λ/a condition is not appropriate as predicted by the simulation.
In summary, the MRE measurements on model phantoms validated the appropriate conditions for accurate and precise MRE found from the simulation study.
Acknowledgements
MRE was performed on a CEA/SHFJ MRI platform affiliated to the France Life Imaging network (grant ANR-11-INBS-0006). SWE was performed at Pitié-Salpêtrière Hospital, Paris, France.References
1. Sinkus R, et al. Viscoelastic shear properties of in vivo breast lesions measured by MR elastography. Magnetic resonance imaging. 2005;23(2):159–165.
2. Baghani A, et al. Theoretical limitations of the elastic wave equation inversion for tissue elastography. The Journal of the Acoustical Society of America. 2009;126(3):1541–1551.
3. Yue JL, et al. Acquisition and reconstruction conditions in silico for accurate and precise Magnetic Resonance Elastography. Physics in Medicine and Biology. In press.
4. Oudry J, et al. Ultrasound-based transient elastography compared to magnetic resonance elastography in soft tissue-mimicking gels. Physics in medicine and biology. 2009b;54(22):6979-6990.
Figures