Synopsis

A novel magnetic resonance elastography (MRE) sequence, combining inversion recovery (IR) with MRE, is introduced to quantify poroelastic properties of biphasic materials. The method is demonstrated on custom-made tofu phantoms featuring biphasic tissue properties with different porosities and elastic moduli. IR-MRE allows for the first time to study the individual fluid and matrix motion in a biphasic medium and the interactions between the two. The same technique applied to in vivo brain also confirms fundamental predictions of poroelasticity theory and demonstrates the transferability of IR-MRE from simple biphasic model materials to complex living tissues.

Introduction

Magnetic resonance elastography (MRE) is a technique to quantitatively measure the mechanical properties of in vivo tissues.

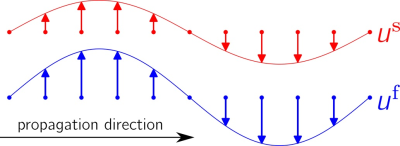
Living soft tissue has a multiphasic complex structure composed of fluid and solid phases. The intricate mechanical interactions between the phases can be analysed based on a biphasic poroelastic medium model, which comprises a solid porous matrix with porosity f saturated by an incompressible fluid (CSF, blood) [1,2,3]. In this model both phases are treated separately as two compartments coupled through a set of motion equations[1]. These equations predict for the shear wave mode, that both the fluid and the solid move with different amplitudes, but identical oscillation phases [1,4] (fig.1):

$$u^f(t) = a\cdot u^s(t) , \alpha \epsilon \mathbb{R}^+$$

Since pores are assumed smaller than the voxel size, the MR signal from each voxel is a superposition of the solid and the fluid partial signals. Conventional MRE only account for effective monophasic media and effective compound displacement fields, resulting in an effective shear modulus ($$$\mu_{effective}$$$).

The aim of this study is to develop the foundations of a methodology that allows decomposition of the displacement fields of the two phases. To achieve this goal we combined a biexponential T1 relaxation model and the biphasic formulation of the MRE signal equation:

$$ S=|S| e⁡^\left(iϕ\right)=S_{solid}+ S_{liquid}= |S_{solid} (TI,f)| e^\left(iϕ_{solid}\right) + |S_{liquid} (TI,f)| e^\left(iϕ_{liquid}\right) $$

Methods

The standard phantom for poroelasticity MRE is tofu[2]. Commercially available tofu might differ from batch to batch and often contains relaxation-time shortening ions. Therefore, we established a production protocol of tofu samples with specific porosity and matrix stiffness based on soy milk and acetic acid(fig.2).

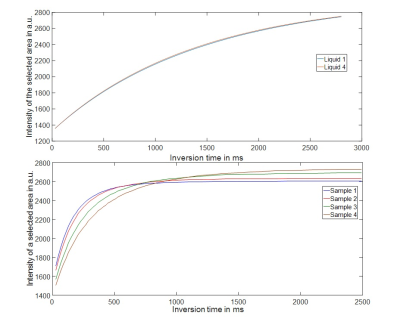
T1_liquid, T1_solid and porosity were estimated for four different samples (fig.2) with different porosity and T1 times by fitting a biexponential T1 relaxation model to a set of conventional inversion recovery scans(fig.3).

MRE was performed in each sample at four frequencies (f=50,60,75,100Hz) and three inversion times (TI=0,600,1500ms) on a 1.5T scanner (Siemens Sonata). For this we developed a new sequence combining inversion recovery (IR) with conventional spin echo EPI MRE (IR-MRE).

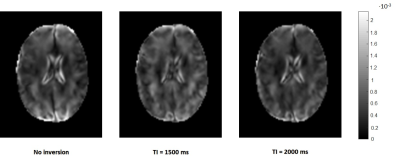
In the second part of the study, we used the same IR-MRE sequence in a 3T scanner (Siemens Trio) to study poroelastic properties of in vivo brain tissue in three healthy subjects. IR-MRE was performed at three mechanical frequencies (30,40,50Hz) and three inversion times (TI=0,1500,2000ms).

Results

IR measurements in four tofu samples yielded T1_liquid=1400ms, and T1_solid=(149,169,222,270)ms (fig.3) and porosities f=(0.06,0.09,0.13,0.19).

In vivo IR-MRE in the brain yielded similar results for strain fields, which are significantly different (p<0.05) at different TI times in most cases (86%)(fig.5).

Discussion

The proposed tofu synthesis protocol enabled us to control the phantom poroelastic and MRI properties, such as porosity, matrix stiffness and the T1-relaxation times. The IR-derived porosities matched an analysis of micrographs (fig.2) demonstrating the applicability of the signal equation(2). Moreover, the measured amplitudes of volumetric and shear strain showed a significant dependence on the inversion time. This implies that inversion time affects the two contributions |S_solid (TI,f)| and |S_liquid(TI,f)| of the two compartments to the measured signal as shown in equation(2). In contrast, the measured effective shear modulus varied with inversion time, which is explained by the definition of the effective shear modulus[1]:

$$ \mu_{effective} = (1-f)\cdot\mu_{solid} $$

This expression shows that, in agreement with our shear wave speed maps shown in fig.4, the measured effective shear modulus reflects changes in porosity and its quantification is not affected by inversion time, as explained in fig.1. The same behaviour is observed in brain images, however, since the microstructure and macrostructure of the brain tissue are much more complicated than tofu the effect is not as pronounced and a statistical analysis is necessary(fig.5).

Conclusion

IR-MRE results confirm that the measured effective shear modulus does not depend on the individual amplitude of fluid or solid motion.

IR-MRE can selectively weight the contributions of the two poroelastic phases to the compound MRE signal and it can be used to measure the dynamics of the two phases separately and more comprehensively than standard MRE.

Acknowledgements

References

1. Hirsch S., Braun J., and Sack I. Magnetic resonance elastography: physical background and medical applications. John Wiley & Sons, (2017).
2. Perriñez, Phillip R., et al. Modeling of soft poroelastic tissue in time-harmonic MR Elastography. IEEE transactions on biomedical engineering 56.3 (2009): 598-608.
3. Leiderman, R., P. E. Barbone, et al. (2006). Coupling between elastic strain and interstitial fluid flow: ramifications for poroelastic imaging. Phys Med Biol 51(24): 6291-313.
4. Biot, M. A. (1956). Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. The Journal of the Acoustical Society of America, 28(2), 168–78