Synopsis

We have developed a finite-volume based elasticity recovery method for Magnetic Resonance Elastography. The method accommodates heterogeneity and compressibility, uses only first derivatives, avoids matrix inversion and can be calculated in a highly efficient stencil format. We compared the method to a Helmholtz-type wave inversion. Visually, the method shows sharper rendering of cracks and boundaries. Quantitatively the values of the new method differ from a Helmholtz-type method in proportion to the severity of interfaces, which likely reflects the new method's sharper rendering. The resolution and sensitivity of the method lower the inherent stability, which we address here with a simultaneous multifrequency wave inversion. Future work will introduce sparsity-promoting regularization to deliver both stability and structure.

Introduction

In recent MR Elastography (MRE) research, more complex material models have grown to widespread use, enabling the incorporation of tissue heterogeneities, the elimination of second derivatives, and the estimation of pressure gradients (e.g. [1] [2] ). Many of these approaches use Finite Element Method (FEM). However, the inversion of elasticity coefficients is represented by hyperbolic first-order PDE models, and it is a well-known mathematical finding that standard FEM methods "cannot approximate satisfactorily first-order PDEs" [3], as they introduce instabilities and spurious oscillations [4,3].

Here we present a novel, simple and fast approach, enabling application of the above modeling assumptions (heterogeneity, first derivatives only, and pressure estimation) while using a mathematically appropriate basis for solving a first-order PDE on a piecewise-constant Cartesian grid such as that found in MRE. We investigate its results in brain and abdomen as compared to a simpler, locally-homogeneous model.

Methods

Finite Volume-Based Method

By considering a novel scheme inspired by Finite-Volume (FV) method, we propose the integration of elasticity equations voxel-wise, obtaining an algebraic representation of the interplay between local parameters to be solved explicitly. Let $$$V$$$ be a single voxel, $$$u$$$ the displacement field, $$$\omega$$$ the excitation frequency, and $$$\rho$$$, $$$G$$$ the voxel-wise constant density and shear modulus. After a quasi-incompressibility relaxation, namely $$$\nabla\cdot u = -\frac{1}{\lambda}p$$$, for a pressure $$$p$$$ and Lamé constant $$$\lambda >> 1$$$, we found that $$ G(V) = -\frac{1}{2 b\cdot b^*} \left( \omega^2 \rho p \cdot b^* + \lambda q \cdot b^* \right) $$ for each voxel $$$V$$$, where $$$b^*$$$ is the complex conjugate of $$$b$$$ and $$ b = \frac{1}{2}\int_{\partial V} (\nabla u + \nabla u^T)n\, ds, \quad p = \int_V u\, dx, \quad q = \int_{\partial V} (\nabla\cdot u) n \, ds $$ This method does not require any matrix inversion and can be extended to compressible elasticity. For this initial investigation, we shall assume that the pressure wave is removed by high-pass filtering.

Subjects

We evaluate the method using two cohorts acquired for previous studies: a cohort of 48 brain acquisitions of healthy subjects whose acquisition methods were described in [5] and a cohort of ten abdominal acquisitions whose acquisition were described in [6]. All acquisitions follow Charité ethical guidelines as described in those papers. The method is compared with the previously published MDEV method, which assumes local homogeneity and no pressure wave. For these initial results we present representative brain and abdomen images, and compare the summary statistics of brain, liver and spleen. Anatomical masks for brain, liver and spleen were generated using the accompanying T2* weighted volumetric image.

Results

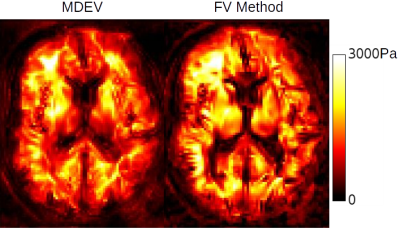
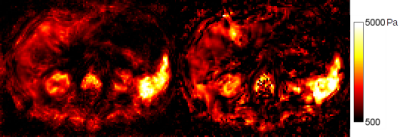
Figure 1 shows a comparison of the same slice of a representative brain acquisition, and Figure 2 shows a comparison of the same slice of a representative abdominal acquisition. Particularly with the brain, a gain in sharpness can be seen, with fluid interfaces more clearly delinated, although there is also a decrease in image stability. This stability is more visible in the noisier abdomen, where stiffness values vary more widely within organs.

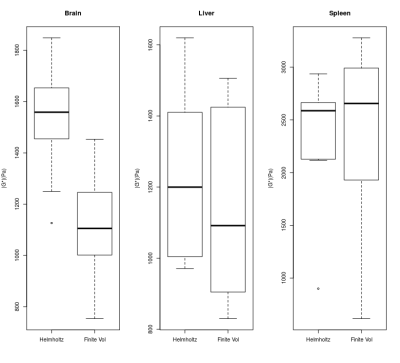
Boxplots for the cohorts of brain, liver and spleen are shown in Figure 3. FV shows slightly higher median spleen estimates than MDEV (2.7 to 2.6 KPa), slightly lower liver estimates(1.1 to 1.2 KPa) and substantially lower median brain estimates (1.1KPa to 1.6KPa).

Discussion

Our scheme simultaneously incorporates numerous much desired assumptions and advantages in MRE: it accommodates tissue heterogeneity, accommodates compressibility, uses only first derivatives, avoids the need for matrix inversion, and because it can be implemented in stencil form, takes negligible processing time. In these respects we consider a Finite-Volume approach a substantial advancement from the Helmholtz and Finite-Element methods presently available.

Differences in reconstruction estimates are common between different numerical methods and this aspect of MRE reconstruction is under increasing study. Here the differences correlate roughly to the frequency and severity of interfaces in the tissue: spleen being quite smooth, liver having larger vessels and brain having fluid-filled sulci. The sharper delineation of interfaces appears to impact the FV method's values when using identical masking and this will need to be accounted for in future work.

We note that the price for delivering a new level of sharpness and specificity, is less local stability. Simultaneous inversion at multiple frequencies aids voxel-wise stability by overdetermination and is worth incorporating, however future work will also develop a sparsity-promoting regularization scheme to simultaneously deliver both stability and fine structure.

Acknowledgements

JM acknowledges CONICYT-PIA-Anillo ACT1416, CONICYT FONDEF/I Concurso IDeA en dos etapas and FONDECYT #1141036 grants. EB acknowledges support of EU FORCE (Horizon 2020, PHC-11-2015) and EU H2020 No 668039, and helpful conversations with Dr. Penny Davies, University of Strathclyde; and Dr. Karsten Urban, University of Ulm.

References

[1] McGarry, M. D. J., Van Houten, E. E. W., Johnson, C. L., Georgiadis, J. G., Sutton, B. P., Weaver, J. B., & Paulsen, K. D. (2012). Multiresolution MR elastography using nonlinear inversion. Medical physics, 39(10), 6388-6396.

[2] Honarvar, M., Sahebjavaher, R., Sinkus, R., Rohling, R., & Salcudean, S. E. (2013). Curl-based finite element reconstruction of the shear modulus without assuming local homogeneity: time harmonic case. IEEE transactions on medical imaging, 32(12), 2189-2199.

[3] Ern, Alexandre, and Jean-Luc Guermond. Theory and practice of finite elements. Vol. 159. Springer Science & Business Media, 2013.

[4] Guermond, Jean-Luc. "A finite element technique for solving first-order PDEs in Lp." SIAM Journal on Numerical Analysis 42.2 (2004): 714-737.

[5] Dittmann, Florian, et al. "In vivo wideband multifrequency MR elastography of the human brain and liver." Magnetic resonance in medicine 76.4 (2016): 1116-1126.