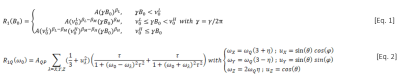5571

T1-dispersion curves modelling and analysis of human glioma resections: a novel biomarker of molecular dynamics

Manuel Petit¹, Sandra Pierre¹, Maxime Leclerq¹, Pascal H. Fries², François Berger¹, Lionel M. Broche³, and Hana Lahrech¹

¹BrainTech Lab - INSERM U1205, Grenoble, France, ²INAC-CEA, Grenoble, France, ³Aberdeen University, Aberdeen, United Kingdom

Synopsis

Here we aim to characterize human glioblastoma with FFC-NMR using cerebral tissue of normal pig as a reference. Power-law models and Fries-Belorisky model (quadrupolar ¹⁴N-¹H coupling peaks (QPs)) were used to analyse the T₁-dispersion. Linear Discriminant Analysis and statistical tests of derived fit parameters were used for classification. T₁ values at low field were found significantly different between cerebral tissues and glioblastoma, a result which is well admitted by the NMR community. However our most relevant finding is the role of the molecular dynamics related parameters to discriminate glioblastoma from cerebral tissues. QPs parameters also appear as a possible biomarkers but require higher signal sensitivity.

Purpose

Fast-Field-Cycling NMR (FFC-NMR) consists in measuring relaxation times T₁ at different magnetic field values at low regime (<1T) and has the unique capability to probe the molecular dynamics of tissues, an information invisible to standard NMR. In our pilot works¹ we have shown the interest in studying glioma by FFC-NMR. Here, using mathematical models, we aim to describe T₁-dispersion curves and to find how the numerical parameters derived either from T₁-dispersion profiles or quadrupolar peaks (QPs of ¹⁴N-¹H nuclei coupling) could be exploited as biomarkers for glioma characterization.

Subjects and Methods

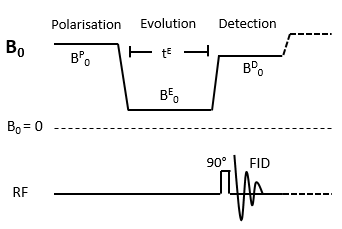
Fig.1 shows FFC-NMR sequence for measuring T₁‐dispersion curves. The magnetisation is polarised at field strength B₀^P, T₁ relaxation occurs during the evolution period t^E at B₀^E and the NMR signal is detected during at B₀^D using the same radiofrequency coil. All experiments were performed with a Stelar relaxometer using 30 B₀^E values [0.1mT-0.5T]. To describe T₁ relaxation, 12 t^E were used for each B₀^E. Acquisition of QPs required 30 magnetic fields values around 58.7mT.

Samples of white and grey matter (WM, GM) of normal pig brains obtained from the Grenoble abattoir were used as references (n=18 (GM) and n=19 (WM), [80-200mg] weight). Human glioblastoma resections (n=5, [30-125mg] weight) were obtained directly from the neurosurgery room under the Biological Resources Center control in charge to manage patient consent and biopsy conservations according to European rules. All samples have been put in dry carbon ice and then in NMR tubes (5mm diameter) filled with Fomblin for FFC NMR acquisitions performed at 37^oC. Hematoxylin/Eosin stain (HE) and Hematoxylin/Eosin/Safran stain (HES) histology were performed to control the nature and grade of resections.

Water and bio-macromolecule interactions are considered to be the main source of relaxation in biological tissue² and T₁-dispersion curves from previous studies were found to fit very well with the power-law model¹, which was therefore re-used here. The model is given in [Eq.1] in three regimes at low, intermediate and high fields. A is the amplitude at the origin; β^L, β^M, β^H the exponents components at low, medium and high fields, known to reflect the molecular dynamics² and ν₀^L, ν₀^H: the discontinuity frequency points at low/intermediate and intermediate/high fields. [Eq.2] is the model that describes the QPs³, where A_QP their amplitude, ω_Q and η parameters that calculate peak frequencies, τ the rotational correlation time; θ and φ the spherical coordinates of the quadrupole vector.

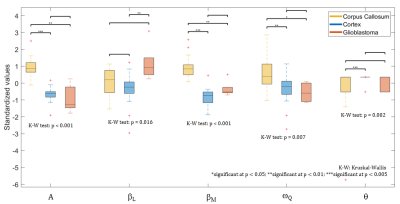
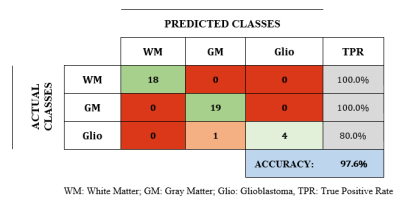
WM, GM and Glioblastoma were classified with a Linear Discriminant Analysis (assuming a normal distribution) and validated using 10-fold cross-validation. The imbalanced dataset situation was solved with a specific cost matrix to penalize the classifier during the training phase. Parameters that could discriminate were pre-selected by the non-parametric Kruskal–Wallis test which investigates the distribution differences between the classes and thus their separability. The five selected features (A, β^L, β^M, ω_Q, θ) were then simplified to retain only the three power-law parameters (A, β^L, β^M). All the analysis was achieved using the software MATLAB, R2017a (Natick, Massachusetts, US).

Results

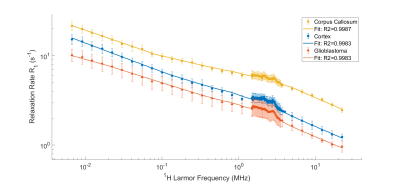
In Fig.2 the mean dispersion curves of human glioblastoma and of pig WM and GM are presented. The curves show a perfect power-law shapes (R>0.99) indicating dominant relaxation by protein matrix². In all curves the signal of QPs is present and accurately fitted to Eq.2. GM and WM curves are well separated and both are clearly distinct from glioblastoma. In Fig.3, differences are quantified by 5 parameters (A, β^L, β^M , ω_Q, θ) pre-selected according the non-parametric Kruskal–Wallis test. However, classification results are equivalent by retaining only A, β^L, β^M parameters achieving a classification rate of 100% for WM and GM and 80% for glioblastoma. This result underlines the fact that low fields accessible by FFC are advantageous to discriminate between normal and diseased tissue.

Discussion/Conclusion

The mathematical models and analysis were found powerful to exploit T₁-dispersion curves. Only one glioblastoma sample was wrongly classified but its histology indicated a low tissue heterogeneity.

The parameter A confirms that T₁ differences at low field are much greater between normal and diseased tissue but this study reveals in particular the role of β^L, β^M parameters to characterize glioblastoma with a new contrast of molecular dynamics.

QPs parameters also appear as possible biomarkers but signal sensitivity should be increased. This work will be extended to understand β^L and β^M correlations with tissue micro-environment changes.

Acknowledgements

No acknowledgement found.

References

1. Broche LM , Huang Y , Pierre S, Berger F , Lurie D J , Fries PF , and Lahrech H, Fast Field-Cycling NMR of human glioma resections: characterization of heterogeneity, ISMRM Honolulu USA (2017)

2. Kimmich, Rainer & Anoardo, Esteban, Field-cycling NMR relaxometry. Progress in Nuclear Magnetic Resonance Spectroscopy, 44. 257-320 (2004).

3. Fries PH, Belorizky E, Simple expressions of the nuclear relaxation rate enhancement due to quadrupole nuclei in slowly tumbling molecules, Journal of Chemical Physics 143 (2015)

Figures

Fig. 1: FFC-NMR sequence for T₁-dispersion curves measurements.

Fig. 2: The two models used to fit the dispersion curves. Eq.1 corresponds to the power-law model to describes the background T₁ - dispersion curve. Eq.2 corresponds to the quadrupolar peaks (QPs) signal.

Fig. 3: Mean R₁-dispersion curves (Relaxation rate R₁=1/T₁ versus ¹H Larmor frequency ν₀=γ/2πB₀^E) of human glioblastoma and of pig WM (Corpus Callosum) and GM (Cortex). The errorbars correspond to one standard deviation. The fits were achieved using both the models presented in Eq. 1 and 2.

Fig. 4: Boxplot of the five selected model parameters. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. The whiskers, bottom and top, indicate the 9^th and 91^th percentiles, respectively. The outliers are plotted using the '+' symbol. The non-parametric Wilcoxon rank sum test was applied to control the null hypothesis that data have equal medians. For visual purposes only standardized values are displayed.

Fig. 5: Confusion matrix of the LDA classification obtained on the testing dataset after the cross-validation. The classification used only three features (A, β^L, β^M). The grey right column indicates the true classification rate per class. The blue cell indicated the true classification rate or accuracy overall. GM and WM are perfectly classified. Glioblastoma has 80% of good classification with one classified as GM.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5571