5500
robust principle component analysis (rPCA) in multi-echo gradient-echo imaging: application in visualizing myelin-related signal without exponential modeling.1Electrical and Electronic engineering, Yonsei University, Seoul, Republic of Korea
Synopsis
In white matter, it is possible to describe multi-echo gradient-echo (mGRE) signal as the summation of multiple exponential decays. However, fitting to this model is sensitive to the error in the raw mGRE signal. In this study, mGRE signal is decomposed to a low rank plus sparsity component using robust principle component analysis (rPCA). Through this, myelin-related signal was extracted without performing exponential modeling. The sparse signal showed myelin-like contrast similar to other mGRE based myelin water imaging.
Purpose
In multi-echo gradient-echo (mGRE) imaging, signal from the white matter has been modeled with multi-component exponential decays. Fitting to this model enables visualizing short T2* components (e.g. myelin water)1. However, multi-exponential fitting is sensitive to error (e.g. noise, damped exponential due to background field2) because of ill-conditioning. In this study, robust principle component analysis (rPCA) was applied to analyze mGRE signals without the need for explicit exponential modeling. Robust PCA is a technique that characterizes the signal into low rank and sparse components3,4,5. For mGRE, the low rank property was used to estimate the slowly varying components that present in the multi-echoes. Sparse components are represented by fast decaying components and imaging artifacts that are noticeable in specific time windows.Method
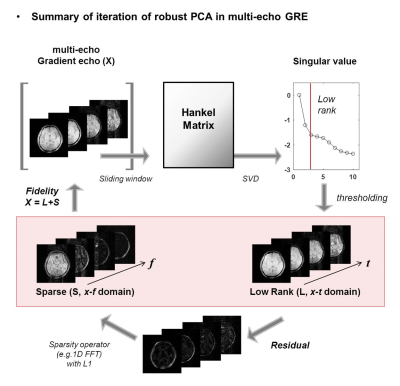
Robust PCA reconstruction Figure 1 shows the overall rPCA algorithm for the given objective. The governing equation is:
$$ \min_{L, S} \parallel X-(L+S) \parallel _2^2 + \mu_1\parallel HL\parallel_* + \mu_2\parallel TS\parallel_1 $$
,where the magnitude of mGRE, X, is decomposed to low rank plus sparse (L+S) components. Temporal hankelization (denoted by H, length of sliding window=10) was applied with nuclear norm (*) over a local region of size 32x32x5. This produces a ‘locally low rank’ effect with pixel-wise Hankelization6. The residual signal was assigned to be a sparse component in x-f domain by using temporal Fourier Transform (T). Equation 1 was implemented by ADMM formulation in MATLAB with following parameters: µ1=0.4, µ2=0.1, Lth (threshold for low rank) = 7th singular value, s(7), Sth (threshold for sparsity) =max{X}*0.1, number of iteration = 20. MATLAB code was implemented by modifying open source4.
MR imaging parameter All experiments were performed on a 3T Siemens scanner. Parameters for mGRE imaging were as follows: matrix size: 128x128x40, spatial resolution 2x2x2 mm3, TR = 120 ms, TE1 = 1.65 ms, ΔTE = 2.08 ms, # of echoes = 45, flip angle = 30°. Total scan time was approximately 10 min.
Analysis of sparse component To investigate the L plus S properties in mGRE, R2*(=1/T2*) of each component was measured through mono-exponential model. Afterwards, the sparse component retrieved from the first echo was compared with myelin water fraction (MWF) extracted from exponential fitting7. Before the reconstructions, a Tukey filter was applied to reduce ringing artifact.
Result
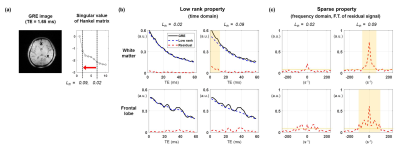
Figure 2 shows the characteristics of low rank plus sparse components in the mGRE signal. Figure 2b shows that low rank enforces the signal to follow the overall envelope of the mGRE signal. Especially, temporal hankelization helps low rank approximation to get signals that have similar envelopes in all time windows. Accordingly, its residual contains fast decaying component (white matter region) and damped signal (frontal lobe) coming from B0 inhomogeneity artifact. In addition, the fast decaying components have sparsity in the frequency domain (Fig. 2c)
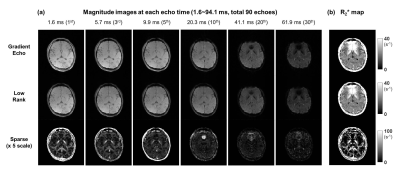
Figure 3 shows the overall results of signal decomposition using rPCA. As shown in Figure 2, sparse components contain fast decaying component at early echoes and B0 artifact at later echoes. At the region of white matter, the T2* of sparse component is 15 ± 18 ms in average which is a slight overestimation comparing with the value in literature for myelin water T2* (10ms) 1.
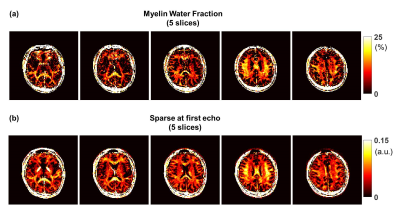
Figure 4 shows the comparison between MWF using three-pool complex model and myelin-related signal retrieval from the rPCA decomposition (i.e sparse component image). Over the white matter regions, the sparse component shows similar distribution and contrast with MWF map (higher values near perpendicular ROIs). Even though sparse component is not quantitative measurement, fluctuation observed in MWF map near frontal lobe (Fig.4a) due to B0 effects is not remarkable in the sparse images.
Discussion
In this study, low rank plus sparse decomposition procedure was applied to mGRE imaging. Through this, a non-exponential myelin water modeling method has been suggested. By avoiding exponential fitting, immunity to B0 artifacts seemed to strengthen. Even though the resulting myelin-related image will be dependent on the threshold value, consistent contrast was observed for a wide range of thresholding values (s(10)<Lth<s(2)). Overall contrast of the sparse component corresponded well to that of MWF except Globus pallidus which could be due to rich iron content. The overestimation at Globus pallidus could be mitigated through complex-value signal analysis similar to MWF with complex modelling7. However, for complex low rank modeling, tissue-oriented phase should be determined precisely at each echo.Acknowledgements
This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT and future Planning (NRF-2015R1A2A1A15052174)References
1. Yiping P. Du, Renxin Chu, Dosik Hwang, Mark S. Brown, Bette K. Kleinschmidt-DeMasters, Debra Singel, and Jack H. Simon. Fast Multislice Mapping of the Myelin Water Fraction Using Multicompartment Analysis of T*2 Decay at 3T: A Preliminary Postmortem Study. Magnetic Resonance in Medicine 58:865–870 (2007)
2. Dmitriy A. Yablonskiy, Alexander L. Sukstanskii, Jie Luo, Xiaoqi Wang. Voxel spread function method for correction of magnetic field inhomogeneity effects in quantitative gradient-echo-based MRI. Magnetic Resonance in Medicine 70:1283–1292 (2013)
3. Ricardo Otazo, Emmanuel Candès and Daniel K. Sodickson.Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic Resonance in Medicine 73:1128–1136 (2015)
4. Benjamin Trémoulhéac, Nikolaos Dikaios, David Atkinson, and Simon R. Arridge. Dynamic MR Image Reconstruction–Separation From Undersampled (k,t)-Space via Low-Rank Plus Sparse Prior. IEEE TMI VOL. 33, NO. 8, 1689-1701 (2014)
5. Evan Levine, Kathryn Stevens, Christopher Beaulieu, and Brian Hargreaves. Accelerated Three-Dimensional Multispectral MRI With Robust Principal Component Analysis for Separation of On- and Off-Resonance Signals. Magnetic Resonance in Medicine, online published (2017)
6. Peng Cao, Xucheng Zhu, Shuyu Tang, Andrew Leynes, Angela Jakary, Peder E.Z. Larson. Shuffled magnetization-prepared multicontrast rapid gradient-echo imaging. Magnetic Resonance in Medicine, online published (2017). 7. Yoonho Nam, Jongho Lee, Dosik Hwang, Dong-Hyun Kim. Improved estimation of myelin water fraction using complex model fitting. NeuroImage 116:214–221 (2015).
Figures