Synopsis

The General Linear Model (GLM) approach is still the standard paradigm used in routine fMRI analysis. This method is based on a model of the BOLD response which depends on the Hemodynamic Response Function (HRF). The HRF ignores the intrinsic intra- and inter-subject variability, resulting in inaccuracies in the brain activity detection. This work leverages on fuzzy sets theory with the purpose of developing a fuzzy GLM to overcome limitations of current GLM-based approaches. We performed an evaluation on simulated and in vivo fMRI data. We compare our results with aproaches based on dictionary learning and wavelet decomposition.

Motivation

Methods and results

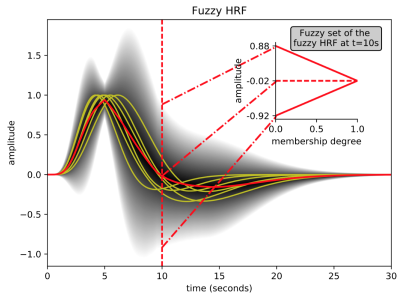
The method developed in this work embeds the fuzzy HRF (Fig. 1) into the fuzzy regression framework with the purpose of performing a fuzzy GLM analysis. The alpha-level set approach and the LR approximations were used to obtain fuzzy GLM parameters estimates. The classical Neyman-Pearson signal detection theory concepts were also extended to the fuzzy paradigm in order to compute statistical activation maps. We compared the performance of the fuzzy GLM method proposed in this work with the classic GLM approach, the Dictionary Learning³, and Wavelet-based methods⁴, over two experiments.

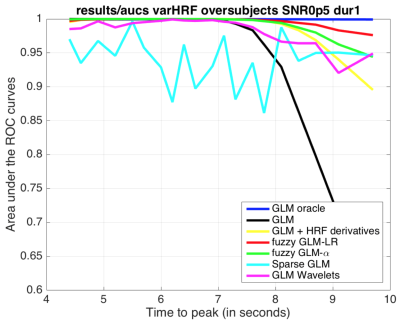
The first experiment uses simulated data, where the true underlying BOLD response is known. We generated a BOLD response for ten thousands brain regions. For each region we used the Glover HRF model, with different values of the $$$\tau_1$$$ parameter. This variation produces times-to-peak in the range 4.36 to 7.48 seconds, and dispertion in the range 3.9 to 6.73 seconds. All the signals were contaminated with noise. Fig. 2 shows the average area under the ROC curve for the different values of the time to peak parameter of the HRF signal. We observe in this figure that the fuzzy methods are uniformly better than the competing methods, and that its performance is close to the oracle. This result shows that the proposed fuzzy approaches are more robust under uncertainty regarding the true specific shape of the HRF signals.

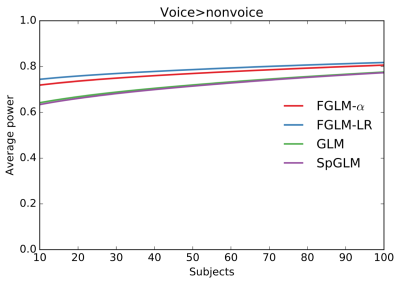
The second experiment uses in vivo fMRI. The data was obtained from the OpenfMRI database⁵. Its acccesion number is ds000158. The data was acquired on two hundred eighteen (n = 218; 117 males; age (mean SD) = 24.1 7.0) healthy adult volunteers. Subjects were exposed to auditory stimuli consisting on voice and non-voiced sounds. Under this setup, temporal voice brain areas shows greater response to voice carrying sounds. Fig. 3 shows the statistical power for the methods, as a function of the number of subjects. We observe that the fuzzy methods have more statistical power than the classic aproach.

This result suggest that the proposed method is able to prevent false negative errors in the boundaries of target brain regions in which BOLD responses should be negligible.

Acknowledgements

This work was supported by the

Advanced Centerfor Electrical and Electronic Engineering, AC3E,

Basal Project FB0008, CONICYT,

Project FONDEF-CONICYT ID16I10322

CONICYT - PIA - Anillo ACT1416

PMI UVA 1402

References

1. Glover GH, Deconvolution of impulse response in event-related BOLD fMRI, Neuroimage. 1999;9:416–419.
2. Möller B, Reuter U. Uncertainty Forecasting in Engineering. Springer-Verlag. 2007.
3. Lee K. et al. A data-driven sparse GLM for fMRI analysis using sparse dictionary learning with MDL criterion. IEEE Transactions on Medical Imaging, 2011;30(5):1076–1089.
4. Meyer, F. et al. Analysis of event-related fMRI data using best clustering bases. IEEE Transactions on Medical Imaging. 2003;22(8):933–939.
5. Pernet, C. et al. The human voice areas: Spatial organization and inter-individual variability in temporal and extra-temporal cortices. Neuroimage; 2015;119:164–174.