5478
A novel phase-based technique to reduce physiological noise in resting state fMRI data1Department of Biomedical Engineering, Amirkabir University of Technology, Tehran, Iran (Islamic Republic of), 2School of Cognitive Sciences, Institute for research in fundamental sciences (IPM), Tehran, Iran (Islamic Republic of), 3Donders Institute for Brain, Cognition and Behaviour, Centre for Cognitive Neuroimaging, Radboud University Nijmegen, Nijmegen, Netherlands, 4Erwin L. Hahn Institute for Magnetic Resonance Imaging, University Duisburg-Essen, Essen, Germany
Synopsis
In this study, a novel phase-based technique is proposed to decrease the effects of physiological noise in resting-state fMRI data. Our technique is based on extracting nuisance components from the phase of fMRI data using spatial-ICA and utilize it to clean magnitude data. To evaluate, we performed the proposed method on Multi-Band fMRI data which benefits from higher temporal resolution to encode physiological effects and compare the efficacy of the technique both with magnitude-based and with RETRIOCOR techniques. Our method has marginal higher identifiability index and
Purpose
Physiological artifacts such as respiration and cardiac-pulsation can significantly reduce BOLD sensitivity in fMRI experiments. This sensitivity reduction is more challenging for the analysis of resting-state (rs)-fMRI data because it cannot benefit from the use of a GLM to suppress physiological noise as is possible for task-related fMRI [1]. To reduce these physiological effects, several studies [2, 3] have recorded physiological data during the experiment in order to regress out the physiological fluctuations. In addition to these techniques, several studies have developed ICA-based techniques using magnitude data to extract regressors related to physiological noise [4, 5]. Nevertheless, phase data is more sensitive to physiological effects compared to magnitude data [6]. Moreover, no extra recording is required to acquire phase data. Here, we propose an approach to extract nuisance components from the phase of fMRI data and utilize it to clean magnitude data for resting-state fMRI application. To evaluate, we performed the method on Multi-Band (MB) fMRI data which benefits from higher temporal-resolution to encode physiological effects and compare the efficacy of the technique both with magnitude-based techniques and with RETRIOCOR [7].Material & Methods
9 resting-state experiments were performed on a 3T Siemens scanner using an MB-EPI-sequence developed by CMRR [8, 9]. Physiological data were also recorded during the experiment using a respiratory-belt and a finger cuff pulse-oximeter. Other imaging parameters were: MB=6, TE/TR =38/593ms, FA=56°, Res=2.5*2.5*2.5mm3, slice-number=42, matrix size=84*84, time-points=1500, Echo-train-length=84, BW=1985Hz.
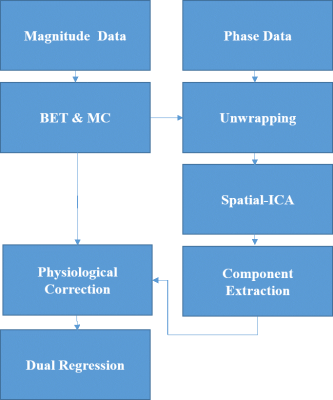
Processing pipeline: First, 4D phase time-courses was mean subtracted (phase of the mean complex image over time) and then temporally unwrapped. Then, motion correction and brain extraction masks, obtained from magnitude data, were applied to the unwrapped phase data. To extract physiological components, spatial-ICA was applied to the phase data. Components were labeled as physiological regressors based on the energy ratio of typical physiological frequencies (>0.2 Hz) to the whole energy spectrum of their time-courses (Threshold =0.5) (Figure 1). To compare with a magnitude-based technique, a similar ICA-based approach was applied to the magnitude data for which the components were selected using the same frequency-based criteria.
For the third approach, a second-order RETROICOR regressor set (8 regressors) along with the RVT regressor were extracted from physiological data. For each regression approach, the physiological regressor set was utilized in a GLM analysis as a nuisance regressor [10], performed in the single-level analysis step. Then, in the group-level analysis step, dual regression was applied to all the subject’s cleaned magnitude data with 1000 permutations using Smith’s resting-state networks (RSNs) [11] as a template. To evaluate the performance, ROI masks were created from the Smith’s RSNs maps by setting the z-score threshold of 2.3 to calculate the statistical measures. The identifiability index (the ratio of the z-score mean value inside to the outside of the RSNs mask) was then computed [5].
Results
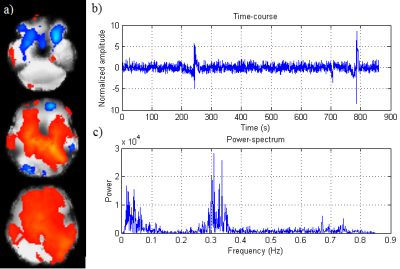
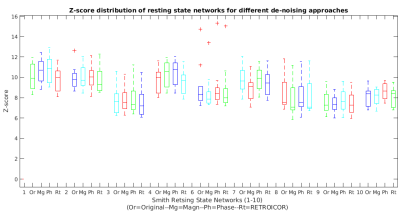
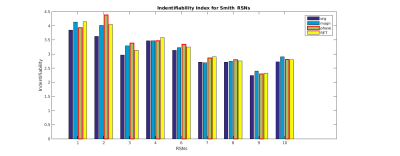
The example of sample spatial maps, related time-course (considered as a physiological regressor) and power spectrum of the typically selected component obtained from the phase data for a representative subject is presented in Figure 2. To compare methods, the identifiability index and the distribution of z-scores achieved from magnitude-based, phase-based and 2nd-order RETRIOCOR+RVT techniques over the masked-ROI were calculated. The results of z-scores (boxplot) and identifiability index for all 3 techniques obtained from dual regression are indicated in Figures 3 & 4 for 9 RSNs. One network out of 10 Smith’s RSNs (RSN#5) was excluded due to insufficient coverage of the related network.
For better comparison, the average values of all three metrics over 9 RSNs including the mean and maximum of z-score along with identifiability index were calculated, shown in Table 1. According to this table, the phase-based technique has the higher average z-scores and identifiability index compared to other techniques across the networks.
Discussion & Conclusion
Two main approaches to reduce physiological artifacts in fMRI are magnitude-based ICA techniques and the RETROIOCOR. A few studies have also used phase-based approaches [10, 12]. Here, we proposed an approach based on extracting nuisance regressors in high temporal resolution phase data using spatial ICA and dual regression. We compared our phase-based approach with 2 other techniques based on the z-scores and identifiability index. Our method has marginal higher identifiability index and average z-score’s mean values compared to magnitude-based and RETROICOR. It should note that average z-score’s mean values drop slightly for magnitude correction and RETROICOR probably due to suppressing a small amount of signal along with noise. To conclude, the proposed method effectively suppresses physiological noise with at least comparable efficiency compared to standard techniques, and with no need to collect physiological data during the experiment.Acknowledgements
No acknowledgement found.References
[1] Caballero-Gaudes, César, and Richard C. Reynolds. "Methods for cleaning the BOLD fMRI signal." Neuroimage 154 (2017): 128-149.
[2] Shmueli, Karin, et al. "Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal." Neuroimage 38.2 (2007): 306-320.
[3] Hagberg, Gisela E., et al. "The effect of physiological noise in phase functional magnetic resonance imaging: from blood oxygen level-dependent effects to direct detection of neuronal currents." Magnetic resonance imaging 26.7 (2008): 1026-1040.
[4] Thomas, Christopher G., Richard A. Harshman, and Ravi S. Menon. "Noise reduction in BOLD-based fMRI using component analysis." Neuroimage 17.3 (2002): 1521-1537.
[5] Pruim, Raimon HR, et al. "ICA-AROMA: A robust ICA-based strategy for removing motion artifacts from fMRI data." Neuroimage 112 (2015): 267-277.
[6] Petridou, Natalia, et al. "Phase vs. magnitude information in functional magnetic resonance imaging time series: toward understanding the noise." Magnetic resonance imaging 27.8 (2009): 1046-1057.
[7] Glover, Gary H., Tie‐Qiang Li, and David Ress. "Image‐based method for retrospective correction of physiological motion effects in fMRI: RETROICOR." Magnetic resonance in medicine 44.1 (2000): 162-167.
[8] Moeller, Steen, et al. "Multiband multislice GE‐EPI at 7 tesla, with 16‐fold acceleration using partial parallel imaging with application to high spatial and temporal whole‐brain fMRI." Magnetic Resonance in Medicine 63.5 (2010): 1144-1153.
[9] Xu, Junqian, et al. "Evaluation of slice accelerations using multiband echo planar imaging at 3T." Neuroimage 83 (2013): 991-1001.
[10] Cheng, Hu, and Yu Li. "Respiratory noise correction using phase information." Magnetic resonance imaging 28.4 (2010): 574-582.
[11] Smith, Stephen M., et al. "Correspondence of the brain's functional architecture during activation and rest." Proceedings of the National Academy of Sciences 106.31 (2009): 13040-13045.
[12] Malekian, Vahid, et al. "Respiratory Noise Reduction in fMRI Data Utilizing Phase Information." ESMRMb Conf., No.893, Vienna (2016).
Figures