5442
Effect of optimised coil-combinations on high-resolution laminar fMRI at 9.4TSriranga Kashyap1,2, Francisco J. Fritz1,2, Robbert L. Harms1, Laurentius Huber3, Dimo Ivanov1,2, Alard Roebroeck1,2, Benedikt A. Poser1,2, and Kâmil Uludağ1,2
1Department of Cognitive Neuroscience, Maastricht University, Maastricht, Netherlands, 2Maastricht Brain Imaging Centre (MBIC), Maastricht, Netherlands, 3Section on Functional Imaging Methods Laboratory of Brain and Cognition, National Institute of Mental Health, Bethesda, MD, United States
Synopsis
Despite the availability of more sophisticated coil-combination methods like Roemer and STARC, ultra-high field fMRI studies still use the conventional sum-of-squares (SoS) method for combining the images of the individual coils from multi-channel RF-coil arrays. Here we use a memory-efficient, CPU/GPU accelerated coil-combine toolbox written in Python to compare and characterise the effect of methods such as covariance-weighted sum-of-squares (CovSoS), Roemer and STARC on sub-millimetre resolution GE-EPI laminar fMRI data acquired at 9.4T, and demonstrate the benefit of using optimised coil-combination for UHF fMRI studies.
Introduction
Ultra-high field (UHF) provides increase in functional contrast-to-noise (fCNR) enabling functional MRI (fMRI) at sub-millimetre resolutions. Some of the acquisition challenges at UHF, such as signal voids, spatially-varying intensity due to Tx/Rx biases, can be partially mitigated using tailored pulse sequences and acquisition strategies1 and improvements in RF technology2. In UHF fMRI acquisitions at high spatial resolutions, the temporal signal instabilities are not dominated by physiological fluctuations. Therefore, fCNR (defined as ratio of BOLD signal amplitude relative to temporal noise) can be improved by optimally combining signals from individual RF channels. Despite the availability of these methods, they have thus far seen limited application in high-resolution fMRI studies. Advanced coil-combination techniques can be computationally expensive in terms of data size and processing time, although this can be alleviated by modern multithreaded programming paradigms. In this work, we use the open-source CPU/GPU accelerated MRI Coil-combine Toolbox (MCT, https://github.com/cbclab/MCT) for all efficient and parallelized coil reconstructions. The aim of this work is to compare and characterize the effect of the different coil-combinations on fMRI data, with a focus on sub-millimetre laminar fMRI at 9.4T.Methods
Data was acquired on a Siemens 9.4T research scanner using an 16Tx/31Rx phased-array coil3 with gradient-echo 3D-EPI4: 0.8mm isotropic resolution, iPAT=3, PE=R>>L, slices=30, TRvol=1440 ms, TE=18 ms, FoV=150 mm, α=12° and PFphase=6/8. The oblique-coronal acquisition slab covered the occipital lobe. A flickering-checkerboard visual stimulation was presented for 20s and with a 40s isoluminant rest period in a block design. Coil-combination: GRAPPA reconstructed magnitude and phase data for the individual channels, as well as raw k-space data were obtained. All data recombination was done using MCT. Individual channel data were converted to x-space complex data per channel (the inverse Fourier transformed k-space) using . The following coil-combination methods were applied: 1. Sum-of-squares (SoS): The signal from the individual channels is combined using the signal itself as a weighting factor. 2. Covariance-weighted Sum-of-squares (CovSoS): The noise covariance matrix across channels was calculated by using the pre-scan noise data5. The x-space complex signal per channel is weighted with respect to its correlation to the other channels (obtained by the inverse of the noise covariance matrix). 3. Roemer (or SENSE R=1): Channel sensitivity profile was estimated as described in [6]. The x-space complex signal per channel is weighted with the inverse of the noise covariance matrix and the channel sensitivity profile. 4. STARC7: A set of weighting factors per channel are computed by optimising the tSNR7 of the channel time-series using the GPU-accelerated Powell optimization routine as implemented in the Multithreaded Optimization Toolbox (MOT)8. The individual channel data are then combined using the optimised weights. The reconstructed data were motion-compensated using ANTs9, GLM-fitted using FSL FEAT and laminarly analysed using CBS-Tools10.Results
The time-series mean illustrates the differences in signal magnitude for the different reconstruction methods (Fig. 1a), with Roemer having more uniformity albeit with lower signal intensity. The effect of the optimised reconstruction methods can be observed in the standard deviation maps of the time-series (Fig. 1b), with Roemer being the most temporally stable, followed by STARC. It follows logically that the tSNR maps (Fig. 1c) exhibit similar trends. The histograms in Fig 2. indicate that STARC and Roemer show most tSNR gains compared to the SoS and that CovSoS shows little to no improvement over SoS. It is important to note that activation was robust across all reconstruction methods with z-scores>2.3 and nearly the same number of activated voxels. Further laminar analyses (Fig. 3) elicit similar BOLD signal profiles for the different reconstruction methods. Computational time with multi-threading in MCT indicates that CovSoS (apart from SoS) is the fastest to reconstruct, followed by Roemer and STARC.Discussion
CovSoS has been shown to be qualitatively better than SoS in UHF diffusion11, although we do not observe a significant difference compared to SoS for fMRI (Fig. 3). STARC is the only approach that computes new weights from the data by explicitly optimising for high tSNR, yielding superior tSNR as expected albeit slightly lower z-scores and %BOLD. Roemer outperforms all optimised reconstruction approaches in terms of signal temporal stability. This work bridges the gap between optimal acquisition and optimal analysis by drawing attention to the importance of optimal coil-combination in UHF fMRI research wherein the thermal noise effects dominate. In conclusion, we make available a fast and efficient open-source toolbox for the community and demonstrate that it can be beneficial for high-resolution fMRI studies to consider suitable coil-combination strategies such as STARC or Roemer instead of the conventional SoS.Acknowledgements
We like to thank Valentin G. Kemper (Maastricht University, Netherlands) for his valuable inputs and discussions regarding 9.4T fMRI. We like to thank David Jangraw (NIH, USA) for sharing his MATLAB implementation of STARC, which was the basis for our reimplementation in Python for the MRI Coil-combine Toolbox. The research was supported by the Netherlands Organization for Scientific Research (NWO) VIDI grants 452-11-002 (KU), 016-178-052 (BAP) and 14637 (AR), and the European Research Council Starting Grant, MULTICONNECT #639938 (AR).References
- Poser, B. A. & Setsompop, K. Pulse sequences and parallel imaging for high spatiotemporal resolution MRI at ultra-high field. NeuroImage (2017). doi:10.1016/j.neuroimage.2017.04.006
- Vaughan, J. T. & Griffiths, J. R. RF Coils for MRI. (Wiley, 2012).
- Shajan, G. et al. A 16-channel dual-row transmit array in combination with a 31-element receive array for human brain imaging at 9.4 T. Magn. Reson. Med. 71, 870–879 (2014).
- Poser, B. A., Koopmans, P. J., Witzel, T., Wald, L. L. & Barth, M. Three dimensional echo-planar imaging at 7 Tesla. NeuroImage 51, 261–266 (2010).
- Triantafyllou, C., Polimeni, J. R. & Wald, L. L. Physiological noise and signal-to-noise ratio in fMRI with multi-channel array coils. NeuroImage 55, 597–606 (2011).
- Roemer, P. B., Edelstein, W. A., Hayes, C. E., Souza, S. P. & Mueller, O. M. The NMR phased array. Magn. Reson. Med. 16, 192–225 (1990).
- Huber, L., Jangraw, D., Marrett, S. & Bandettini, P. A. Simple approach to improve time series fMRI stability: STAbility-weighted Rf-coil Combination (STARC). in ISMRM (2017).
- Harms, R. L., Fritz, F. J., Tobisch, A., Goebel, R. & Roebroeck, A. Robust and fast nonlinear optimization of diffusion MRI microstructure models. NeuroImage 155, 82–96 (2017).
- Avants, B. B. et al. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage 54, 2033–2044 (2011).
- Bazin, P.-L. et al. A computational framework for ultra-high resolution cortical segmentation at 7Tesla. NeuroImage 93, 201–209 (2014).
- Fritz, F. J. et al. High resolution diffusion MRI and tractography of post mortem human brains using kT-dSTEAM at 9.4T. in OHBM (2017).
Figures
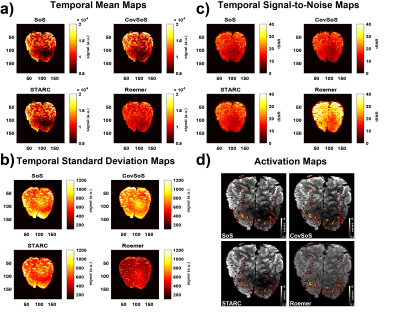
Figure 1. Representative single-subject maps of (a) mean over the
functional timeseries i.e. temporal mean, (b) temporal standard deviation, (c)
temporal signal-to-noise (tSNR) defined as temporal mean/temporal standard
deviation and (d) activation maps overlaid on mean EPI image (scaled
identically) of the corresponding reconstruction method.
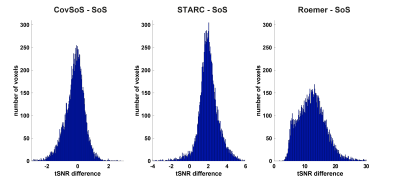
Figure 2. Difference histograms of tSNR of
optimised coil-combine approaches relative to SoS.
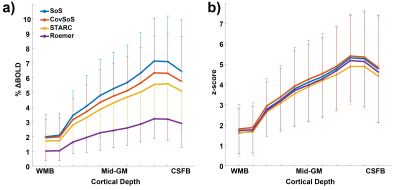
Figure 3. Laminar profiles
of (a) BOLD signal change and (b) z-scores, sampled from the activated portion
along the upper bank of the calcarine sulcus (V1) across cortical depths. Error
bars indicate standard deviation of the signal in each layer.