5441

High SNR Functional MRI Using Oscillating Steady State Imaging

Shouchang Guo¹ and Douglas C. Noll²

¹Electrical and Computer Engineering, University of Michigan, Ann Arbor, MI, United States, ²Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States

Synopsis

Signal-to-noise ratio (SNR), a limiting factor for functional MRI, can be improved by through the use of higher magnetic fields or through the use of array coils. This work proposes a novel acquisition scheme for BOLD fMRI that has the potential to improve SNR by a factor of 2 or more. This approach uses an oscillating steady state signal that is T2*-weighting and when combined across the period of oscillation produced robust fMRI results in both 2D and 3D imaging experiments.

Introduction

Quadratic phase sequences in conjunction with a constant gradient dephasing are a well-recognized approach for establishing a spoiled steady state. ¹ In this work, we propose to use quadratic phase sequences with balanced gradients to exploit the large, but oscillating steady state signal available prior to gradient dephasing. These signals contain approximately twice the RMS signal amplitude of spoiled sequences and thus, can dramatically improve the signal-to-noise ratio (SNR). For a particular range of parameters, the oscillating steady state (OSS) signals are T2*-weighted and are suitable for BOLD functional MRI. The oscillating nature and short TR places some limitations on FOV, spatial resolution and/or temporal resolution, but due to their reproducible nature, the oscillations can be modeled in the reconstruction process which should allow acquisitions in comparable time to BOLD imaging.

Theory and Methods

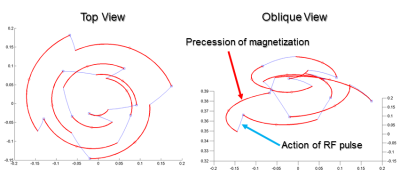
Balanced steady-state imaging generally uses a constant phase increment to achieve spin-echo-like and, depending on the FA and TR, T2/T1-weighted contrast. ² The specific frequency locations of the nulls and peaks in the spectral response can be made to vary via a linearly varying phase increments: $$\phi(n) - \phi(n-1) = 2 \pi \frac{n}{ n_c},$$ leading to a quadratic phase sequence with periodicity $$$n_c$$$ TRs. If the phase increment is kept small ($$$n_c > 120$$$), the spin-echo contrast is preserved. ³ However, for larger phase increments, a new oscillating steady state emerges. An example of magnetization progression for a spin with off-resonance 20 Hz, T1 = 1300ms, T2 = 75ms, FA = 10 degrees, TR= 15ms, and $$$n_c =10$$$ is shown in Fig. 1. Off-resonance shifts lead to similar temporal waveforms but shifted in time. This phase progression is equivalent to a spoiling seed of 36 degrees. With spoiling gradients, one gets the average of all isochromats yielding a small net signal, but balanced gradients lead a large, but oscillating signal. Averages of moderate distributions of spins lead to modest reductions in signal strength, equivalent to some T2’- or T2*-weighting. For the parameters in Fig. 1, simulations show that the T2’-weighting is equivalent to 22ms at the beginning of the readout and 34ms at the end of the readout interval.

Experiment data were collected on a GE MR750 scanner, and for the oscillating steady state used FA = 10 degrees, TR= 15ms, $$$n_c = 10$$$, and a fully sampled spiral-out acquisition with diameter 35 samples, though other parameters can yield similar results. Phantom studies are used to demonstrate the principles of the oscillating steady state using balance gradients as well as with spoiling gradients. Human functional MRI studies were performed using a right-handed finger tapping task (20s on/20s off x 4 cycles) analyzed by correlation with a reference waveform. Both single-slice 2D and 12-slice 3D imaging were acquired. The $$$n_c = 10$$$ oscillations are combined by taking the 2-norm of 10 consecutive image time points, yielding a temporal resolution of 150ms ($$$n_c * TR$$$) and 1.8s ($$$n_c * n_z * TR$$$) for the 2D and 3D acquisitions, respectively. RETROICOR ⁴ with externally acquired respiration and cardiac signals was applied to 40s blocks was used to eliminate physiological noise in the functional data. Standard 2D BOLD imaging using a spiral-in readout was acquired for comparison.

Results

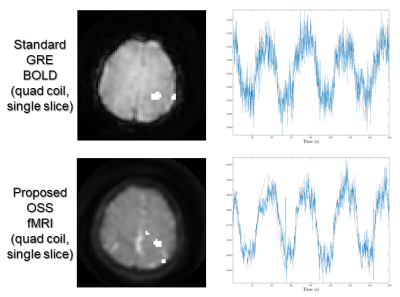
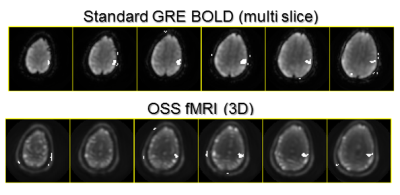
Figure 2 shows signals from a phantom study using both balanced and unbalanced gradients. Note that the average signals for the oscillating steady state are substantially higher than the spoiled sequence. Figure 3 shows fMRI results with a 2D acquisition with for a single slice of the OSS and standard BOLD acquisition using a single-channel head coil. While the spatial SNR was much higher, the temporal SNR was only about 68% higher, perhaps due to uncorrected physiological variations. Figure 4 shows both 3D OSS and BOLD fMRI results for in motor cortex.

Discussion and Conclusions

OSS imaging is a fundamentally new acquisition method for high-SNR, T2*-weighted imaging. We demonstrate that the oscillations can be combined for robust fMRI results in both single-slice 2D and 3D acquisitions. Without the spoiling gradients, the resultant RMS signal strength is between 68% and 200% larger when compared to standard (spoiled) gradient echo imaging, which offers potentially a dramatic improvement in SNR. Higher resolution studies, which are more thermal noise limited, should benefit the most. Drawbacks of the OSS method include sensitivity to physiological noise and encoding inefficiency due to the short TR and oscillating signals. Physiological noise can be estimated and removed using standard techniques, while encoding inefficiencies can be addressed through the use of model-based reconstruction methods that exploit the reproducible nature of the oscillations.

Acknowledgements

This work was supported by NIH Grant R01EB023618.

References

1. Zur, Y., Wood, M. L., & Neuringer, L. J. (1991). Spoiling of transverse magnetization in steady‐state sequences. Magnetic resonance in medicine, 21(2), 251-263.

2. Bernstein, M. A., King, K. F., & Zhou, X. J. (2004). Handbook of MRI pulse sequences. Elsevier.

3. Foxall, D. L. (2002). Frequency‐modulated steady‐state free precession imaging. Magnetic resonance in medicine, 48(3), 502-508.

4. Glover, G. H., Li, T. Q., & Ress, D. (2000). Image‐based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magnetic resonance in medicine, 44(1), 162-167.

Figures

Figure 1. Periodic motion of magnetization through RF pulses and free precession for an off-resonance frequency of 20 Hz, T1 = 1300ms, T2 = 75ms, FA = 10 degrees, TR= 15ms, and $$$n_c =10$$$ from two different views. Signal intensity varies as magnetization towards and away from the center in the left panel.

Figure 2. Images of steady state with quadratic phase progression ($$$n_c = 10$$$) with (a) spoiling gradients and (b) balance gradients (OSS). Each panel has 10 images across the periodic phase pattern and is shown twice to demonstrate the reproducibility. (c) Time courses for the center voxel in the phantom for the spoiled (blue) and oscillating steady states (red). The moving root-mean-square (RMS) average of 1 period (10 images) of the OSS shows a signal strength roughly three times larger than the spoiled signal.

Figure 3. Single-slice, quadrature coil acquisition using standard BOLD (upper panel: spiral-in, TR = 150ms, TE = 30ms) and oscillating steady state (lower panel: spiral out, TR = 15ms, $$$TE_{eff}$$$ = 22ms) with matched resolution. The OSS data are presented as the RMS sum across 1 period of oscillations with effective temporal resolution of 150ms. Note similar areas of activation, but better temporal SNR with the OSS method. Temporal SNR was 95 and 160 and percent signal change 4.1% and 3.3% for BOLD and OSS, respectively.

Figure 4. Functional MRI of six slices drawn from multislice 2D BOLD (upper panel: spiral-in, TR = 1.8s, TE = 30ms) and 3D oscillating steady state (lower panel: spiral out, volume TR = 1.8s, $$$TE_{eff}$$$ = 22ms) showing similar activation patterns.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5441