5422
FETAL CORTICAL PARCELLATION BASED ON GROWTH PATTERNS1Department of Computer Science and Technology, Shandong University, Jinan, China, 2Department of Radiology and BRIC, University of North Carolina at Chapel Hill, Chapel Hill, NC, United States, 3DTIC, Universitat Pompeu Fabra, Barcelona, Spain, 4ICREA, Pg. Lluis Companys 23, 08010, Barcelona, Spain, 5Fetal i+D Fetal Medicine Research Center, BCNatal, Hospital Clı́nic and Hospital Sant Joan de Déu, Barcelona, Spain
Synopsis
The available cortical parcellations created for adults are inapplicable for fetuses, due to dramatic differences in brain appearances and dynamic growth of fetal brains. Considering sulcal-gyral landmarks are not stably established in fetal brains, we propose to use the growth patterns of cortical properties to parcellate fetal cortical surfaces. Growth patterns, which reflect underlying changes of microstructures, enable an accurate definition of distinct regions in development and function, as microstructures determine the molecular organization and functional principles of the cortex. We apply the growth-
Introduction
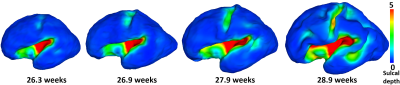
Cortical parcellation aims to divide the cerebral cortex into a set of regions that are distinct in structure, function, and connectivity, which plays an important role in region-based and network-based neuroimaging analysis1. Conventional sulcal-gyral landmarks based parcellations1 on adult brains are not suitable for the fetal brain, due to the unestablished and rapidly developing cortical folds2,3 (as shown in Fig. 1). Meanwhile, the dynamic growth patterns of cortical properties (e.g., surface area, cortical thickness, and myelin content) in fetus reflects the underlying changes of cortical microstructures, which essentially determine the molecular organization and functional principles of the cerebral cortex4,5. Therefore, we propose to unprecedentedly parcellate the fetal cortical surfaces based on the dynamic growth patterns of cortical properties to better reflect the underlying microstructural boundaries, which fills both technical and knowledge gaps in fetal cortical parcellation.Methods
T2-weighted MR images were acquired from 25 healthy fetuses between 26 and 29 gestational weeks. HASTE sequences were used with the following parameters: TE = 82 ms, TR = 1500 ms, and voxel size = 0.5 × 0.5 × 2.5 mm3. Each subject had 4 axial, 2 coronal, and 2 sagittal 2D scans. First, for each subject, we reconstructed a high-quality 3D image6 and segmented each 3D image7. Second, we applied our developed tools for cortical surfaces reconstruction8, co-registration9. Third, we resampled each cortical surface to a standard mesh tessellation, thus establishing inter-subject vertex-to-vertex cortical correspondences for each cortical vertex. Fourth, we computed its surface area and further spatially smoothed it10. Fifth, we sorted all fetal cortical surfaces by age and constructed the growth trajectory of surface area at each vertex, since surface area is the most dynamic growing surface property in fetus. To comprehensively capture both the low-order and high-order similarities of growth patterns of vertices, we constructed two similarity matrices. The first similarity matrix was defined as the Pearson’s correlation (scaled to [0, 1]) of the growth trajectories between each pair of vertices on surface. The second similarity matrix was defined as the Pearson’s correlation (scaled to [0, 1]) of the growth correlation profile between each pair of vertices on surface. For each vertex, its growth correlation profile was defined as the Pearson’s correlation coefficient between its growth trajectory of surface area and that of each of the reference points. The reference points were 320 uniformly sampled vertices on two cortical hemispheres. To effectively leverage the information of the two similarity matrices, we used a nonlinearly fusion method11 to fuse these two similarity matrices together for the parcellation using spectral clustering12, thus better capturing both their common and complementary information.Results
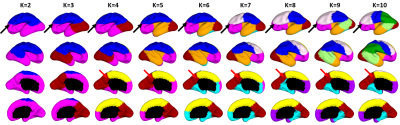
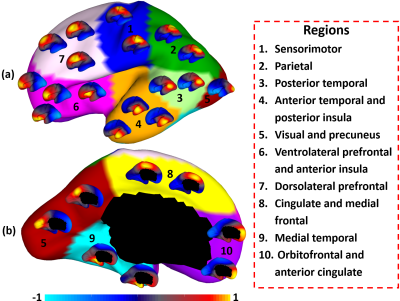
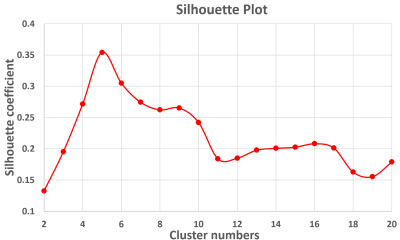
Fig. 2 shows the parcellation results with different cluster numbers from 2 to 10 using our proposed method, which shows biologically meaningful cortical regions. At 2-clusters parcellation, the proposed method identifies a dorsal-ventral division. With increase of the cluster numbers, the proposed method reveals a meaningful hierarchical organization of the growth patterning of surface area. For example, the boundaries between the ventrolateral and dorsolateral prefrontal regions (as indicated by black arrows) are well-preserved from 2-clusters to 10-clusters; the boundaries between the precuneus cortex and paracentral lobule (as indicated by red arrows) appear in 4-clusters, and well preserve to 10-clusters. Moreover, the parcellation results present relatively symmetric patterns on the left and right hemispheres from 2-clusters to 10-clusters. Fig. 3 shows seed-based analysis of the correlation maps of growth patterns of surface area, by using 25 uniformly distributed seeds on the surface. In Fig. 3, seeds in the same cluster yield largely the similar correlation patterns, while seeds across the boundaries of clusters lead to quite different patterns, indicating that our parcellation is meaningful. Fig. 4 shows the silhouette coefficients of our parcellation results with cluster numbers from 2 to 20. The highest silhouette coefficient corresponds to 5-clusters. After that, the coefficient reaches a stable plateau from 6- to 10-clusters, and then decreases significantly after 10-clusters. To capture the detailed regionalization of growth patterns of surface area, we adopted 10-clusters parcellations as shown in Fig. 3, where all clusters largely correspond to structurally and functionally meaningful specializations, with their approximated names shown in right columns in Fig. 3.Discussion and Conclusion
We proposed a novel cortical parcellation method based on the growth patterns of cortical properties for fetus. We derived the first set of fetal cortical surface parcellation maps based solely on dynamic growth patterns of surface area. In the future, we will combine other cortical properties for fetal cortical parcellation.Acknowledgements
This work was partially supported by NIH grants (MH108914, MH107815).References
1. Desikan, R.S., et al., An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31(3):968-980.
2. Studholme, C., Mapping fetal brain development in utero using magnetic resonance imaging: the Big Bang of brain mapping. Annu Rev Biomed Eng. 2011;13:345-368.
3. Benkarim, O.M., et al., Toward the automatic quantification of in utero brain development in 3D structural MRI: A review. Hum. Brain Mapp. 2017.
4. Dubois, J. and G. Dehaene-Lambertz, Fetal and postnatal development of the cortex: MRI and genetics. Toga AW In: Brain Mapping: An Encyclopedic Reference. Waltham, MA: Academic Press (Elsevier). 2015;11-19.
5. Clouchoux, C., et al., Quantitative in vivo MRI measurement of cortical development in the fetus. Brain Struct Funct. 2012;217(1):127-139.
6. Kuklisova-Murgasova, M., et al., Reconstruction of fetal brain MRI with intensity matching and complete outlier removal. Med Image Anal. 2012;16(8):1550-1564.
7. Sanroma, G., et al. Building an ensemble of complementary segmentation methods by exploiting probabilistic estimates. in MICCAI-MLMI. 2016.
8. Li, G., et al., Measuring the dynamic longitudinal cortex development in infants by reconstruction of temporally consistent cortical surfaces. Neuroimage. 2014;90:266-279.
9. Yeo, B.T., et al., Spherical demons: fast diffeomorphic landmark-free surface registration. IEEE Trans Med Imaging. 2010;29(3):650-668.
10. Li, G., et al., Mapping region-specific longitudinal cortical surface expansion from birth to 2 years of age. Cereb Cortex. 2012;23(11):2724-2733.
11. Ng, A.Y., M.I. Jordan, and Y. Weiss. On spectral clustering: Analysis and an algorithm. in NIPS. 2002.
12. Wang, B., et al., Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods. 2014;11(3):333-337.
Figures