5406
Anatomically-informed and patient-specific diffusion tensor sampling schemes for the cervical spinal cord1Vanderbilt University Institute of Imaging Science, Vanderbilt University, Nashville, TN, United States, 2Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 3Philips Healthcare, Baltimore, MD, United States, 4Electrical Engineering and Computer Science, Vanderbilt University, Nashville, TN, United States, 5Radiology and Radiological Sciences, Vanderbilt University, Nashville, TN, United States
Synopsis
In this study, we minimize uncertainty in Diffusion Tensor Imaging (DTI) parameters by optimally selecting diffusion gradient directions utilizing prior structural knowledge. By measuring the anatomy of the spinal cord for each subject, we created patient-specific, anatomically-informed DTI encoding schemes for 256 subjects, utilizing just 6 diffusion directions. In addition, we create an optimal encoding 6-direction scheme for the anatomically-average person. Through simulations and experimental validation on a physical fiber phantom, we show improvements in FA estimation, even when compared to conventional 30 direction schemes. This technique results in minimal scan time and increased accuracy in order to maximize clinical value.
Introduction
Clinical implementation of human spinal cord DTI requires fast, accurate, and reproducible measurements of the tensor and derived contrasts. Here, we utilize known anatomical information to create patient-specific diffusion encoding schemes; this maximizes the reproducibility of DTI measurements, while minimizing scan time by using just six encoding directions.
In the brain, diffusion gradients are usually applied uniformly over a sphere1 due to the largely uniform orientation of white matter structures. However, in the spinal cord, several groups have utilized prior knowledge of the spinal cord anatomy – typically assuming either straight fibers oriented superior/inferior, or a “cone” of fibers within an angular tolerance – in order to minimize variances in estimating the fiber orientation2, fractional anisotropy (FA)3,4, or mean diffusivity (MD)4. In this study, instead of assuming structural information, we make detailed measurements of the spinal cord orientation distribution in 256 subjects, creating both patient-specific optimized schemes, as well as a scheme optimized for the anatomically-average person.
We show through simulation that FA error is reduced when compared to a uniformly distributed 6-direction scheme. We then experimentally validate these techniques using a fiber phantom, where the variance is less than that of a 30-direction DTI scheme.
Methods
Imaging was performed on a 3T whole body Philips scanner on 256 healthy subjects. A high-resolution structural image was acquired for each subject using a T2-weighted turbo-spin echo sequence (resolution=0.5*0.5mm, slice thickness=2mm) in sagittal orientation. The mid-sagittal slice was used to identify spinal cord corresponding to C1-C6, from which an orientation distribution (with respect to the field-of-view) was defined. To derive an orientation in an anatomically-relevant frame, this distribution was calculated with respect to the cord perpendicular to the center of C3 (which is how we typically plan diffusion scans).
This patient-specific anatomy was simulated with 1000 cylindrical tensors (parallel diffusivity = 1.9E-3 mm2/s, perpendicular diffusivity = 0.5E-3 mm2/s, from 5) with primary eigenvectors distributed according to the patient distribution. The optimization method starts with a default 6-direction scheme, and uses simulated annealing to minimize total variance of FA, and modifies the 6 directions after each iteration, resulting in a patient-specific optimized scheme. For the anatomically-average person, the cumulative spinal cord distribution was used as the primary eigenvector distribution as input to the optimization algorithm.
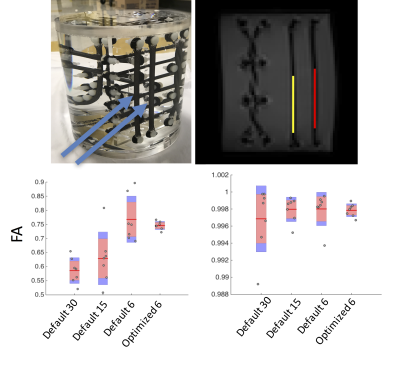
Finally, for experimental validation, an anisotropic diffusion phantom (Synaptive Medical) was scanned using 7 repeats each of uniformly distributed 30-direction, 15-direction, and standard 6-direction schemes, as well as 7 repeats of a scheme optimized for the orientation distribution of two bundles in the phantom. ROIs were used to assess the mean and variance of FA in each physical bundle.
Results
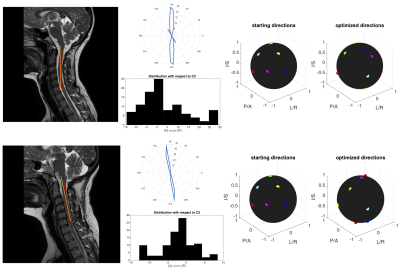
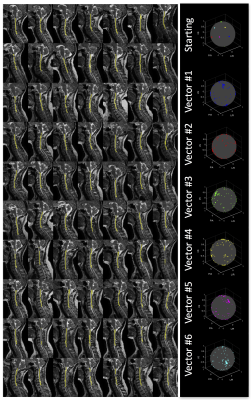
Figure 1 shows two exemplar processing pipelines. In each, the spinal cord (C1-C6) is segmented, and the anatomical distribution is derived. The starting 6-direction scheme and optimized patient-specific scheme for each are shown. Simulated tensors for each subject anatomy suggest a reduction in FA variance by 41% and 32%, respectively. This pipeline was repeated for 256 subjects (Figure 2, left, shows 70 subjects), creating 256 patient-specific schemes (Figure 2, right).
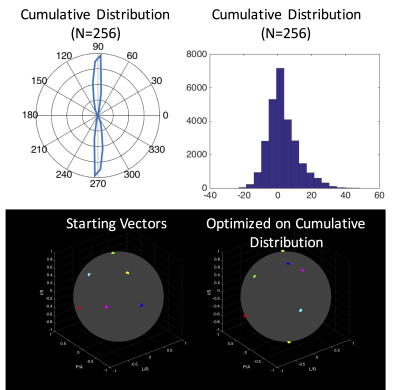
The average
subject anatomy is shown in Figure 3. The average anatomy is relatively aligned
with the cord nearest C3, within +/- 20°. The optimized acquisition scheme for
the average subject is shown in Figure 3, which shows a reduction in FA error
by 39% compared to the conventional 6-direction set.
Finally, diffusion data acquired on a phantom were assessed in two bundles oriented in a superior/inferior direction. Plots of the median FA for all 7 repeats are shown in Figure 4. For ROI #1, the variance in FA across repeats is 2.1E-3, 8.8E-3, 6.8E-3, and 0.2E-3 for the 30, 15, 6, and optimized 6-direction schemes, respectively. For ROI #2 (a bundle with anisotropy FA ~= 1), the variance in FA across repeats is very small, 1.5E-5, 0.2E-5, 0.3E-5, and 0.6E-6, respectively. Thus, in both cases, the reproducibility of the optimized scheme is greater than that of all others.
Discussion and Conclusion
In this study, we have optimized the diffusion tensor encoding scheme for the cervical spinal cord using structural information. Through simulations, this results in patient specific DTI protocols, as well as a 256-person average optimized scheme, all of which show increased accuracy in estimating FA. These techniques are empirically validated on a physical phantom, which shows reduced variation in FA estimates in two fiber bundles. These techniques can be used to minimize scan time, and also increase fidelity of DTI estimates of tissue microstructure, both of which are critical to implementation of DTI in the clinic.Acknowledgements
This work was supported by the National Institute of Neurological Disorders and Stroke of the National Institutes of Health under award numbers RO1 NS058639, R21 NS087465, and R01 EB017230. Additionally, support has been provided by the National MS Society and the Conrad Hilton Foundation. We also acknowledge Synaptive Medical for loan of the phantom.References
1. Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 1999;42(3):515-525.
2. Yanasak N, Allison JD, Zhao Q, Hu TC, Dhandapani K. Non-uniform gradient prescription for precise angular measurements using DTI. Med Image Comput Comput Assist Interv. 2008;11(Pt 1):866-873.
3. Peng H, Arfanakis K. Diffusion tensor encoding schemes optimized for white matter fibers with selected orientations. Magnetic resonance imaging. 2007;25(2):147-153.
4. Majumdar S, Zhu DC, Udpa SS, Raguin LG. A diffusion gradient optimization framework for spinal cord diffusion tensor imaging. Magnetic resonance imaging. 2011;29(6):789-804.
5. By S, Smith AK, Dethrage LM, et al. Quantifying the impact of underlying measurement error on cervical spinal cord diffusion tensor imaging at 3T. Journal of magnetic resonance imaging : JMRI. 2016;44(6):1608-1618.
Figures