Synopsis

The ability to detect specific changes in tumour tissue using diffusion-weighted (DW) MRI microstructural models depends on the accuracy and precision of parameter estimates, as well as the magnitude of specific biological changes. This work investigates the SNR requirements that data must meet in order to yield sufficiently precise estimates for detecting apoptotic cell shrinkage. Given the relative changes in cell size, R, and intracellular volume fraction, f_i, as a result of apoptosis, simulations indicate that detecting changes in R require ~4-fold higher SNR than detecting changes in f_i. Comparing the magnitude of biological changes with measurement accuracy and precision should form part of the validation process for potential biomarkers.

Introduction

Diffusion-weighted (DW) MRI microstructural model parameters potentially provide a more specific characterisation of tumour tissue than phenomenological parameters such as the apparent diffusion coefficient (ADC)^1,2. In particular, estimating cell size, R, and volume fraction, f_i, potentially allows different forms of cell death to be distinguished, as they affect R and f_i in different ways; for example, cell shrinkage is a hallmark of apoptosis³.

The success of using microstructural models to distinguish between distinct microstructural changes depends on the accuracy and precision of model parameter estimates, as well as the magnitude of specific biological changes. For example, if typical changes in R are smaller than the precision with which R can be estimated, such changes will not be detected. This work investigates the signal-to-noise ratio (SNR) required for obtaining sufficiently precise estimates such that apoptotic cell shrinkage can be detected.

Methods

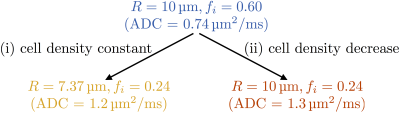
The PGSE signal was modelled analytically by combining restricted diffusion inside a sphere with hindered extracellular diffusion, with five parameters: cell radius, R, intracellular volume 
fraction, f_i, intra- and extra-cellular diffusivities, D_i and D_e, and T₂. Starting from a plausible ‘baseline’ model of tumour tissue with R = 10 
μm, f_i = 0.60, two possible microstructural changes were considered: (i) mimicking apoptosis (cell size decrease, cell density constant)⁴ and (ii) mimicking a loss of cells (cell density decrease); see Figure 1. In addition, equivalent changes were applied to two other 'baseline' microstructures, with different initial cell sizes (R=13 
μm, f_i=0.60, and R=7 
μm, f_i=0.60). D_i = 1 μm²/ms, D_e = 2 μm²/ms and T₂ = 125 ms were assumed for all microstructures^2,5.

Similar to the resolution limit for axonal diameter estimates⁶, we define the ability to detect a change in a parameter, p, in terms of a two sample z-test, with α = 0.05:

$$\sqrt{\mathrm{SE}^{2}_{p_1} + \mathrm{SE}^{2}_{p_2}} \leq \frac{\Delta p}{1.96} \quad\quad\quad\quad\quad\quad (1)$$

where $$$\mathrm{SE}_{p_n}$$$ is the standard error on the nth estimate of parameter p, and $$$ \Delta p = |p_2 - p_1|$$$ is the magnitude of the parameter change; p={R, f_i}, n={1, 2}. The effect of SNR on $$$\mathrm{SE}_{p_n}$$$ was evaluated using Monte Carlo simulations with noisy synthetic data, generated from the microstructures using an optimised⁷ clinical acquisition, extending the approach described previously⁸ (Figure 2). The model was fitted to the noisy signals (with SNR defined based on the b = 0 s/mm² signal at TE = 100 ms), here focussing on fits with D_i and D_e fixed to their ground truth values, for simplicity. $$$\mathrm{SE}_{R_n}$$$ and $$$\mathrm{SE}_{f_{{i}_{{n}}}}$$$ were estimated as the standard deviation of 1000 iterations, excluding fits with extreme values (within 1% of the fit constraints).

Results and discussion

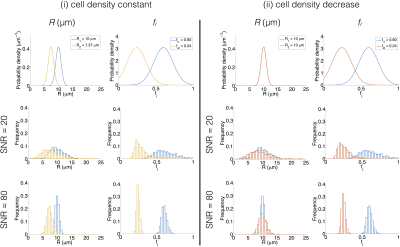
Figure 3 (top row) illustrates the theoretical broadest Gaussian PDFs consistent with successfully resolving the changes in R and f_i. At SNR = 20, precision depends on the microstructure, but is sufficient to detect the change in f_i in both cases (Figure 3, middle row). However, SNR is insufficient to detect the change in R for case (i), implying that the two cases cannot be distinguished. At SNR = 80, precision varies less between different microstructures, and is sufficient to detect the change in R, for case (i), and changes in f_i, for cases (i) and (ii) (Figure 3, bottom row).

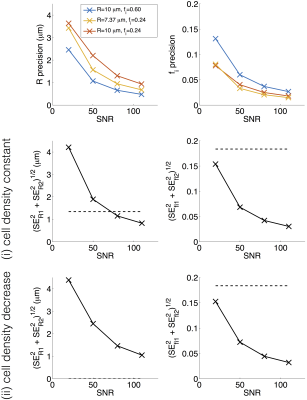
Figure 4 (top row) plots $$$\mathrm{SE}_{R}$$$ and $$$\mathrm{SE}_{f_{{i}}}$$$ against SNR, for the three microstructures. In addition to the general trend to better precision at higher SNR, generally R is estimated more precisely at higher f_i, and f_i estimated more precisely at lower f_i. Figure 4 (middle/bottom rows) plots the ‘resolution limit’ (Equation 1, left hand side) against SNR. Dashed lines show the threshold (Equation 1, right hand side), indicating that SNR ≈ 80 is required for detecting ∆R in case (i) while SNR < 20 is sufficient for detecting ∆f_i in both cases.

Similar trends were observed for the two other ‘baselines’, suggesting that the findings may be generalised to other microstructures. Similar results were also observed for other PGSE acquisitions, suggesting that the general trends are not dependent on the scan parameters. Note that these results reflect a best-case scenario, as D_i, D_e, and T₂ are assumed to be known and unchanging.

Conclusion

Acknowledgements

References