5378
q-Space Novelty Detection in Short Diffusion MRI Scans of Multiple Sclerosis1Department of Informatics, Technical University of Munich, Munich, Germany, 2Physics Department, Technical University of Munich, Munich, Germany, 3CUBRIC, Cardiff University, Cardiff, United Kingdom, 4Department of Neurology and Psychiatry, Sapienza University of Rome, Rome, Italy, 5Division of Psychological Medicine and Clinical Neurosciences, Cardiff University, Cardiff, United Kingdom
Synopsis
Diffusion MRI can capture disease-related microstructural changes, but most methods use handcrafted data transformations that discard parts of the information and require quite long scan times. In contrast, q-space novelty detection (q-ND) circumvents these drawbacks, and does not require any knowledge whatsoever about the effect of disease on q-space measurements. Instead, q-ND highlights voxels that look unlike anything seen in a database of healthy scans. Here we show that novelty scores from q-ND largely coincide with multiple sclerosis lesions, and that q-ND also works at reduced scan times.
Introduction
So far, establishing the relationship between q-space measurements and microstructure has required mathematical/physical representations which are suboptimally simplistic (discarding parts of the information) and rely on unstable fitting procedures requiring quite long scan times. Moreover, some kind of prior knowledge about disease-related effects is required. In contrast, handcrafted-representations-free methods1,2 circumvent most of these drawbacks. In particular, q-space novelty detection2 (q-ND) does not even require any knowledge whatsoever about the effect of disease on q-space measurements. Instead, it highlights voxels that look unlike anything seen in a database of healthy scans. Here we apply q-ND to scans of multiple sclerosis (MS) patients. We compare voxel-wise novelty scores from q-ND with lesion labels obtained without diffusion MRI, and for the first time study the effect of scan time reduction on q-ND results.Methods
The data were as follows:3 As the the healthy database to compare the patient datasets with, we used 26 diffusion MRI scans of healthy volunteers: six b=0 images, 40 uniformly-distributed diffusion directions (bmax=1200s/mm2, SE-EPI, voxel size 1.8mm×1.8mm×2.4mm, matrix 128×128, 57 slices, TE=94.5ms, TR=16s, motion/distortion-corrected,4 upsampled to 256×256×172). Using machine-learning nomenclature, we refer to these 46 volumes (six b=0, 40 diffusion-weighted) as “channels”. As test data, we used scans of five MS patients (scan parameters as above). Lesions were marked by human raters in additional structural T2-weighted scans for comparison with q-ND results. In order to avoid potential discrepancies in image intensity across scans, we divided each scan by its mean intensity. Additionally, in order to prevent some channels from dominating over others in novelty detection, we divided each channel by the channel-wise mean taken across all scans (a technique known as “feature scaling”).
We consider every voxel as a data sample. In the standard setting, the feature vector consists of the 46 q-space measurements. In additional evaluations, we used small random subsets of the channels in order to study the effect of reducing the scan time. This results in an n-dimensional feature space, where n≤46 is the size of the chosen set of channels. Selected channels are the same for both reference and test data. For every test data sample, we define the novelty score in arbitrary units as the distance between its feature vector and the closest, in terms of Euclidean distance in feature space, feature vector corresponding to a voxel from the healthy database. Consequently, the more dissimilar the test point is to healthy voxels, the higher its novelty score. This translates to the following formula for the novelty score: r(x)=miny∈Y‖x−y‖, where Y is set of feature vectors y corresponding to healthy voxels in the n-dimensional feature space, and ‖·‖ is the Euclidean norm. We took only brain voxels into account in the healthy database and in the tested images. To speed up q-ND runtime, we reduced the reference dataset size by randomly sampling 1/6 of brain voxels from each scan.
Results
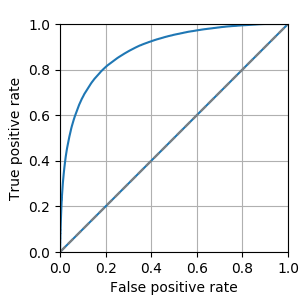
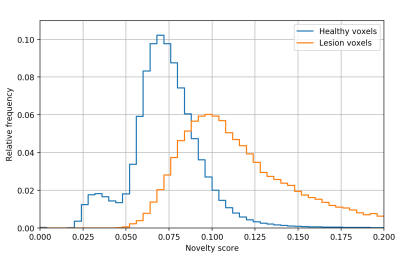
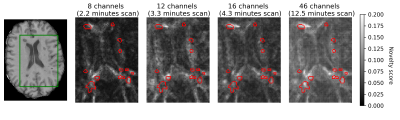
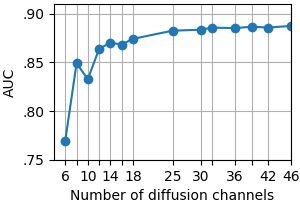
Fig. 1 shows the receiver operating characteristic (ROC) for MS lesion segmentation across all test voxels using all 46 channels. The area under the curve (AUC) is 0.888, indicating a promising performance. The per-patient AUC ranged from 0.599 (for a patient with particularly small extent of lesions) to 0.929. Fig. 2 shows the normalized histogram of novelty score outputs on the test set for 46 channels. Figures. 3 and 4 show how reducing the number of sampled channels (and thus reducing the scan time) affects the quality of the results.Discussion
These results show that high novelty scores largely coincide with MS lesions even with a small number of channels and thus short scan duration. Moreover, certain random subsets of channels (containing useful and complementary information) yield better results than others. Some imperfections in the predictions may be due to imperfections of the method, or imperfections of image registration; on the other hand, some apparent imperfections of predictions might be rather due to imperfections of the lesion labels used for reference.Conclusions
Our experiments show that by using q-space novelty detection it is possible to directly segment multiple sclerosis lesions from raw diffusion MRI data without fitting handcrafted representations and without requiring hand-marked labels. (Note that here lesion labels were used here merely for validation.) The approach that we use shows promising segmentation even at short scan times (Figs. 3-4). Moreover, we do not need to acquire labels which can be imperfect. To summarize: the method marks any q-space signal as a deviation from healthy data if this signal is affected by the disease in a measurable way.2 And this happens without any representations-based assumptions or prior knowledge of the disease effect on the q-space signal. Other novelty detection methods5 could be tried.Acknowledgements
This work was supported by the ERC Consolidator Grant "3DReloaded".References
1. V. Golkov et al. q-Space deep learning: twelve-fold shorter and model-free diffusion MRI scans.IEEE Trans Med Imag. 2016;35(5):1344–1351.
2. V. Golkov et al. Model-free novelty-based diffusion MRI.Proc IEEE Int Symp Biomed Imag (ISBI). 2016:1233–1236.9
3. I. Lipp et al. Comparing MRI measures of myelin changes in multiple sclerosis. Org Human Brain Mapping (OHBM) Annual Meeting. 2017:3060.
4. S. Klein et al. elastix: A toolbox for intensity-based medical image registration. IEEE Trans Med Imag. 2010;29(1):196–205.
5. M.A. Pimentel, et al. A review of novelty detection. Signal Processing. 2014;99:215–249.
Figures