Synopsis

Diffusion- and kurtosis tensor estimators generally assume independent and a Gaussian distributed noise. While with adequate signal-to-noise ratios (SNR) this assumption can be made without significant bias in the estimated models, this is not true when utilizing high diffusion weighting thus low SNR. In such case, the Rician noise should be considered with maximum likelihood (ML) estimators for example. Moreover, the mathematical properties of ML estimators could unveil novel details of the underlying diffusion process within the brain. In this work, we present super-fast, GPU accelerated ML estimator with Matlab interface to provide a practical tool for such improved estimation.

Introduction

Widely used diffusion tensor¹ estimators rely on solving a least squares problem that assumes the noise is independent and follow a Gaussian distribution which is only approximately true for high signal-to-noise ratio (SNR) diffusion weighted images (DWI)². While the issue of Rician distributed noise has been previously addressed with maximum likelihood (ML) estimators^3,4, the problem in the clinical use of these more complex yet potentially more accurate algorithms has been their long computational times. A recent study⁵ used a clever data augmentation to reduce this time but, nevertheless, the tensor model estimation for a full-brain DWI acquisition could still take multiple hours even with a modern CPU workstation depending on how many DWIs were acquired.

In this work, we implemented the expectation maximization (EM) algorithm⁵ in CUDA programming language to parallelize the voxelwise ML estimation with GPU. The algorithm was written in single and double precision to enable the efficient use of the low- and the high-end workstations. We developed an easy-to-use Matlab interface for the GPU-estimator that handles the data transfer between CPU and GPU so the user does not necessarily need to understand CUDA language. We benchmarked the ML estimator with simulations using the widely applied linear least squares (LLS) and iteratively re-weighted linear least squares (IWLLS)⁶ algorithms and recorded fractional anisotropy (FA)⁷, kurtosis anisotropy (KA)⁸, and estimation times.

Methods

Full-brain DWI simulations based on diffusion- and kurtosis tensors from the ground truth (GT) sample⁹ were generated using b-values 1000s/mm² and 2500s/mm² and 60 nearly uniformly distributed gradient directions¹⁰ with ten non-diffusion weighted images.

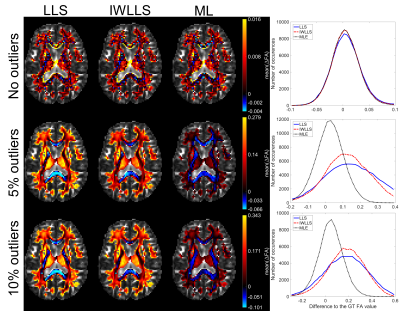
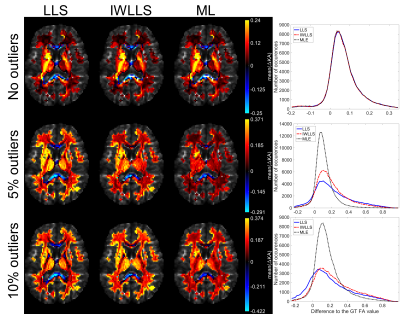
The largest white matter (WM) structures were cropped as the region of interest by applying a threshold of 0.15 on GT FA image. In the first simulation, no outliers were introduced before adding the Rician noise with SNR 35. In the second and the third simulations, 5% and 10% of the WM signals were replaced with full -100% signal decrease artefacts before adding the noise. Each simulation with random noise generation and outlier selection from both q-space shells was repeated 100 times.

Diffusion model based on DT and KT was estimated for these noisy DWIs with LLS, IWLLS⁶, and the high-speed ML⁵ estimator. FA and KA⁸ values were calculated from tensors and compared with the GT values.

Results and Discussion

Figure 1 visualizes the mean errors for FA estimates calculated over the 100 noise iterations in different white matter structures. In the case of no outliers (first row), errors remain negligible for all estimators. When outliers were introduced to the WM diffusion signals, both LLS and IWLLS estimates become biased whereas the expectation of the ML estimate remains near the average GT value. While ML underestimate the FA values in the high FA region such as corpus callosum more than IWLLS, the degree of underestimation remains overall low in comparison with the overestimations by LLS algorithms. Figure 2 shows respective results for the KA estimates.

The average voxelwise computing times for LLS, IWLLS, GPU-ML, and a reference ML reported in another study⁴ were 0.05ms, 0.66ms, 2.75ms, and 200ms, respectively. Both LLS and IWLLS estimations were done using a quad core CPU running at 4600MHz clock speed whereas ML estimation was performed on a GPU with 2048 CUDA cores running at 1178MHz. While the GPU accelerated ML estimator was approximately four times slower per voxel than IWLLS algorithm, it produced less biased estimates in the presence of outliers. Moreover, with a multi-GPU-workstation the average estimation time could easily be halved as the parallelization of the voxelwise estimation with the Matlab interface is easily improved. Notably, GPU-ML estimator was 70 times faster than the reference ML estimator⁴.

Conclusion

In this study, we presented a high-speed ML estimator for diffusion and kurtosis tensor models. The developed easy-to-use Matlab interface eliminates the necessary need for the user to understand the CUDA programming language and allows the fast implementation of this algorithm in various software as a robust alternative to widely used least squares estimators.

While the original EM algorithm was already relatively fast, our new GPU-based implementation finally brings this mathematically more versatile estimator to clinically sensible speed. As this work focused on the accelerated algorithm, following studies will be carried out to evaluate the differences between the ML estimate and robust least squares estimates^11–13. It should be noted that the here presented algorithm does not constrain the estimates based on any physical limits and thus could potentially be made even more robust by applying such limits³ or outlier detection during the diffusion MRI data preprosessing¹⁴.

Acknowledgements

References

1. Basser, P. J., Mattiello, J. & Lebihan, D. Estimation of the Effective Self-Diffusion Tensor from the NMR Spin Echo. J. Magn. Reson. Ser. B 103, 247–254 (1994).

2. Salvador, R. et al. Formal characterization and extension of the linearized diffusion tensor model. Hum. Brain Mapp. 24, 144–155 (2005).

3. Veraart, J., Van Hecke, W. & Sijbers, J. Constrained maximum likelihood estimation of the diffusion kurtosis tensor using a Rician noise model. Magn. Reson. Med. 66, 678–686 (2011).

4. Landman, B., Bazin, P.-L. & Prince, J. Diffusion Tensor Estimation by Maximizing Rician Likelihood. Proceedings. IEEE Int. Conf. Comput. Vis. 1–8 (2007).

5. Liu, J., Gasbarra, D. & Railavo, J. Fast estimation of diffusion tensors under Rician noise by the EM algorithm. J. Neurosci. Methods 257, 147–158 (2016).

6. Veraart, J., Sijbers, J., Sunaert, S., Leemans, A. & Jeurissen, B. Weighted linear least squares estimation of diffusion MRI parameters: Strengths, limitations, and pitfalls. Neuroimage 81, 335–346 (2013).

7. Basser, P. J. & Pierpaoli, C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. 111, 209–219 (1996).

8. Poot, D. H., den Dekker, A. J., Achten, E., Verhoye, M. & Sijbers, J. Optimal experimental design for diffusion kurtosis imaging. IEEE Trans Med Imaging 29, 819–829 (2010).

9. Froeling, M., Tax, C. M. W., Vos, S. B., Luijten, P. R. & Leemans, A. ?MASSIVE? brain dataset: Multiple acquisitions for standardization of structural imaging validation and evaluation. Magn. Reson. Med. 77, 1797–1809 (2017).

10. Jones, D. K., Horsfield, M. A. & Simmons, A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn. Reson. Med. 42, 515–525 (1999).

11. Mangin, J. F., Poupon1, C., Clark, C., Le Bihan, D. & Bloch, I. Eddy-current distortion correction and Robust tensor estimation for MR diffusion imaging. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2208, 186–194 (2001).

12. Chang, L. C., Walker, L. & Pierpaoli, C. Informed RESTORE: A method for robust estimation of diffusion tensor from low redundancy datasets in the presence of physiological noise artifacts. Magn. Reson. Med. 68, 1654–1663 (2012).

13. Tax, C. M. W., Otte, W. M., Viergever, M. A., Dijkhuizen, R. M. & Leemans, A. REKINDLE: Robust Extraction of Kurtosis INDices with Linear Estimation. Magn. Reson. Med. 73, 794–808 (2015).

14. Oguz, I. et al. DTIPrep: quality control of diffusion-weighted images. Front. Neuroinform. 8, 4 (2014).