5341

Comparison of Navigator-free Multi-shot Diffusion-Weighted Imaging Reconstruction Algorithms for EPI
Malte Steinhoff1,2, Kay Nehrke3, and Peter Börnert3,4

1Braunschweig University of Technology, Braunschweig, Germany, 2University of Lübeck, Lübeck, Germany, 3Philips Research Europe, Hamburg, Germany, 4Dept. Radiology, LUMC, Leiden, Netherlands

Synopsis

Multi-shot diffusion-weighted MRI allows for higher spatial resolution than single-shot approaches, but suffers from image artifacts due to motion-induced shot-specific phase variations. Advanced parallel imaging reconstructions can mitigate these effects, but a comparison of these approaches is still missing, especially for the widespread EPI. Following the concept of reproducible research, a number of algorithms were implemented, adapted and refined for EPI, and compared in simulations and in-vivo. Results show different performance and applicability. The iterative feedback and the sharing of joint global information in the reconstruction and appropriate constraints were found to be crucial for high-quality high-resolution DWI.

Introduction

Diffusion is a key contrast in neurological and oncological applications. To increase the spatial resolution of currently preferred single-shot diffusion-weighted techniques (DWI), multi-shot approaches were proposed, which severely affect image quality, mainly due to motion-induced shot-to-shot phase variations1. For correction, phase navigators2 were proposed, which however are adding undesired complexity and increasing SAR. In contrast, advanced parallel imaging reconstructions1,3 can estimate the phase, data driven, for each interleaf using SENSE4,5. This information, if included into a global reconstruction, can avoid corresponding image artifacts. Comparisons of such algorithms have been focused mainly on spiral trajectories, but not in detail for the more widespread EPI scheme. In this work, which supports the concept of reproducible research, various algorithms were implemented and refined with focus on EPI, and are compared in simulations and in-vivo.

Methods

Three multi-shot DWI algorithms (SENSE+CG1, POCS-ICE3 and the Newton’s Method approach6) were studied. All are estimating the motion-induced phase maps for each uniformly under-sampled EPI shot using SENSE4,5, assuming their spatial smoothness and including them into a global reconstruction model3,7 as shown in Fig. 1. Additionally, all shots are assumed to share an equal magnitude image.

(1) SENSE+CG1 can be interpreted as a two-step SENSE approach: first estimating phase maps $$$\phi_\xi$$$, second estimating the image $$$\mathbf{\rho}$$$ from all data. Each shot is reconstructed in full resolution, using SENSE, applying median filtering (9x9 kernel) and a maximum of 12 iterations to estimate the shot-specific phases once. The global reconstruction performed subsequently uses the phase maps as fixed input and iterates at most 10 times.

(2) POCS-ICE3, conversely, iterates over the phase estimation in the global reconstruction by including the current global image and phase maps as a guess for the next phase estimations. This iterative feedback in POCS-ICE was adapted here to EPI. The corresponding POCS-ICE parameters were set according to Guo et al.3.

(3) Newton’s Method alternately optimizes the shot-wise and global convex functional using Newton iterations6, partly inspired by PR-SENSE8. In the present work, the inversion of the Hessian matrix is circumvented using nested Conjugate Gradient6 (CG) methods. After a global optimization, the subsequent reconstruction of shot $$$\xi$$$ is initialized by the current shot image guess $$$\mathbf{\rho}_\xi = \phi_\xi \mathbf{\rho}$$$. Phase maps $$$\phi_\xi$$$ were extracted in half resolution using median filtering (kernel 9x9). Maximum iteration numbers were set to 12 and two for the nested shot-wise and global CGs, respectively, and the feedback was done at most 50 times.

Algorithms were evaluated in simulations using a BrainWeb9 phantom, disturbed by simulated phase errors8, assuming eight receive coils, radially distributed around the head. Gaussian noise was added to the coil images before shot-specific undersampling. Simulations were executed with $$$SNR=\{5,10,15,20\}$$$ and segmentations $$$N_{Shots}=\{2,3,4,5,6,7,8\}$$$. Performance was averaged over ten randomly disturbed phantoms. In addition, DWI-EPI measurements were performed in five healthy volunteers (3T Philips Ingenia). Informed consent was attained, according to the rules of the institution. The data was acquired using 1.0 mm² in-plane resolution, a b-value of 1000 s/mm² and between four and six segments employing 13 receive coils.

All algorithms were implemented in Python 3.6.0 to run on 2.66 GHz Intel Core2 Duo CPU with 4 GB RAM. Convergence was assumed when the residual error3 of subsequent iterations fell below 10-8 in simulations and 10-6 in-vivo or maximum iteration number was reached.

Results

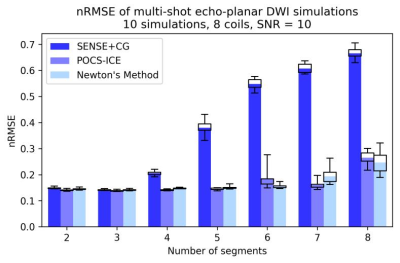
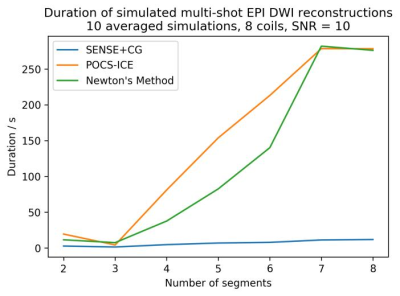
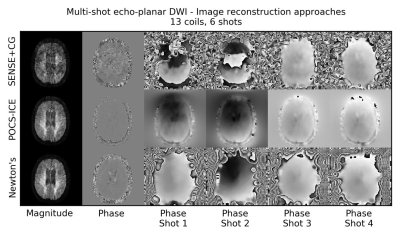
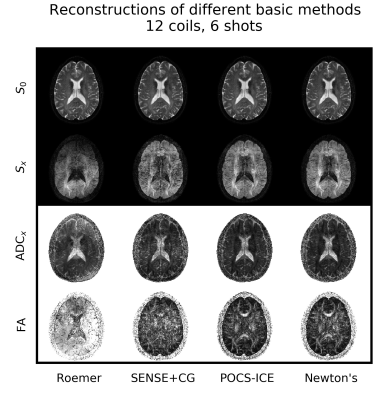
Figure 2 shows the reconstruction errors for varying segmentation. For low segmentations, all methods perform similarly. For higher shot numbers, the error of POCS-ICE and Newton’s Method increases slowly, whereas SENSE+CG gets tremendously compromised. Figure 3 shows the associated average duration of the three algorithms. SENSE+CG is by far the fastest method. For moderate segmentation, Newton’s Method is about two times faster than POCS-ICE. Figure 4 shows estimated in-vivo phase maps. Some SENSE+CG phase estimates are strongly compromised by the high g-factor and the significant variation of signal energy in the different EPI shots. Figure 5 shows some in-vivo results.

Discussion

The present results for EPI are generally consistent with previous studies1,3 for spiral trajectories. Unlike spiral segmentation, EPI shots, although uniformly subsample k-space, contain different energy which influences reconstruction stability and convergence. Therefore, iterative feedback with phase updates and same magnitude constraint are found to be crucial for good image quality. For low segmentation, SENSE+CG provides a fast and cheap solution with comparable quality. For higher segmentation, Newton’s Method and POCS-ICE provide high-performance reconstructions, whereby Newton’s Method is faster and POCS-ICE is more robust against noise.

Although the performance of these parallel imaging driven approaches is promising, further effort is necessary to ease clinical adoption.

Acknowledgements

No acknowledgement found.

References

1) Truong TK, and Guidon A. High‐resolution multishot spiral diffusion tensor imaging with inherent correction of motion‐induced phase errors. Magnetic resonance in medicine. 2014; 71(2): 790-796.

2) Jeong HK, Gore JC, Anderson AW. High‐resolution human diffusion tensor imaging using 2‐D navigated multishot SENSE EPI at 7 T. Magnetic resonance in medicine. 2013; 69(3): 793-802.

3) Guo H, Ma X, Zhang Z, Zhang B, Yuan C, Huang F. POCS‐enhanced inherent correction of motion‐induced phase errors (POCS‐ICE) for high‐resolution multishot diffusion MRI. Magnetic resonance in medicine. 2016, 75(1): 169-180.

4) Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k‐space trajectories. Magnetic resonance in medicine. 2001, 46(4): 638-651.

5) Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magnetic resonance in medicine. 1990, 16(2): 192-225.

6) Vogel, CR. Computational methods for inverse problems. Society for Industrial and Applied Mathematics, 2002.

7) Liu C, Moseley ME, Bammer R. Simultaneous phase correction and SENSE reconstruction for navigated multi‐shot DWI with non‐cartesian k‐space sampling. Magnetic resonance in medicine. 2005, 54(6): 1412-1422.

8) Hu Z, Ma X, Truong TK, Song AW, Guo H. Phase‐updated regularized SENSE for navigator‐free multishot diffusion imaging. Magnetic resonance in medicine. 2017, 78(1): 172-181.

9) Brainweb: Simulated Brain Database, http://www.bic.mni.mcgill.ca/brainweb/. Accessed July 27, 2017.

Figures

Figure 1: Shot-wise and global discrete, linear models for DWI reconstruction. Here $$$\xi$$$ is the shot index, $$$\mathbf{d}$$$ denotes the measured data vector, $$$F$$$ the generalized Fourier operator, $$$C$$$ the coil sensitivities, $$$\mathbf{\rho}$$$ the image and $$$\Phi_\xi$$$ represents the motion-induced, shot-specific phase estimates. $$$A$$$ is the joint matrix of Fourier, phase and sensitivity encoding. The shot-wise phase maps $$$\Phi_\xi$$$ are estimated using parallel imaging and integrated into the global model $$$A$$$.

Figure 2: Final normalized root mean square error (nRMSE) of three multi-shot DWI algorithms with varying EPI-shot segmentation in simulations. The whiskers of the boxplots contain the full range of results. POCS-ICE and Newton’s Method iteratively update the phase maps using the same magnitude constraint, whereas SENSE+CG estimates the phase maps for the global model just once.

Figure 3: Reconstruction time for the three multi-shot DWI algorithms in simulations with varying EPI-shot segmentation. The algorithms were stopped in iteration $$$i$$$ when $$$nRMSE_i/nRMSE_{final}<10^{-4}$$$ to attain the associated averaged durations.

Figure 4: Final images and four phase maps reconstructed by SENSE+CG, POCS-ICE and the Newton’s Method approach for a six-shot EPI in-vivo data set. (top row) Form left to right SENSE+CG magnitude and phase results are shown, followed by the reconstructed phase maps of shots 1-4. (middle row) Corresponding results for POCS-ICE and (bottom row) for Newton’s Method, respectively. Please note the total energy content of the EPI shots (1-6) was 13%, 5%, 8%, 21%, 31% and 23%, respectively. Thus, shot 1 has the least, whereas shot 4 has the most energy, which explains the problems of SENSE+CG to estimate proper phase maps.

Figure 5: In-vivo results of four different reconstruction algorithms for a six-shot EPI DWI data set with three diffusion directions (not all are shown). In vertical direction, reconstructed images without ($$$S_o$$$) and with diffusion weighting (b = 1000s/mm²) in x-direction ($$$S_x$$$), ADC maps in x-direction and FA maps calculated from three diffusion directions are shown. In horizontal direction, the algorithms Roemer, SENSE+CG, POCS-ICE and the Newton’s Method approach are listed. Roemer applies the SNR-optimal5 sensitivity-weighted sum of the joint data sets stacked from all shots ignoring thereby shot-wise phase variations, resulting in signal drop outs.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5341