Synopsis

Intravoxel Incoherent Motion (IVIM) parameter mapping yields quantitative information about diffusion and pseudo-perfusion properties. In brain IVIM, parallel imaging with two-fold undersampling has been reported. In order to address noise amplification and unfolding artifacts at undersampling factors greater than two with parallel imaging, reconstruction in spatio-principal component space with data reshuffling (k-b_pp PCA) is presented here. Using in-vivo brain data, it is demonstrated that k-b_pp PCA allows for significantly increased undersampling factors relative to parallel imaging while maintaining comparable image quality and parameter estimation errors.

Introduction

The Intravoxel Incoherent Motion (IVIM) [1] model has successfully been used clinically [2,3] to map perfusion in the brain. So far, parallel imaging with undersampling factors of R=2 using GRAPPA has been applied to shorten readout durations. Parallel imaging, however leads to noise amplification, which increases exponentially beyond a given g-factor limit [4,5]. In order to address this limitation in practice, redundancy among the images within an IVIM dataset can be exploited. The regularized image reconstruction technique of k-t PCA [6] which operates in the spatio-principal component space may be utilized, as for example demonstrated in parameter mapping applications [7].

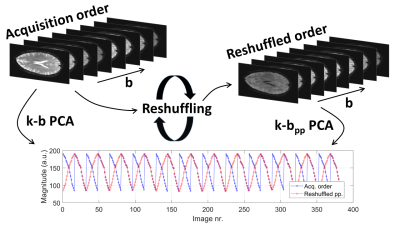
It is the objective of the present work to implement and validate k-t PCA for brain IVIM. The method is referred to as k-b PCA to account for the diffusion encoding strength b as encoding dimension. An additional modification is introduced to implement pseudo-periodic (pp) reshuffling of images along the b encoding dimension before reconstruction for higher sparsity in the spatio-principal component space, termed k-b_pp PCA, see Figure 1. In-vivo brain IVIM parameter maps of diffusion (D), perfusion fraction (f) and pseudo-diffusion (D*) acquired in healthy subjects are compared to maps derived from parallel imaging (SENSE) and fully sampled data.

Subjects and Methods

Iterative k-t PCA [8] was adapted and implemented to reconstruct IVIM data in Matlab (Mathworks, USA). In k-b PCA, all acquired data including all diffusion encoding directions and strengths together with all signal averages are concatenated in acquisition order along the "temporal" direction. In k-b_pp PCA, every second set of ascending b-values of the same diffusion encoding direction is reversed to achieve a pseudo-periodic signal. In both methods, data consistency using the forward encoding operator $$$E$$$, image estimate $$$\vec{i}$$$ and acquired k-space data $$$\vec{d}$$$ is enforced along with a regularization term to incorporate information from low-resolution training data $$$^{x-pc}M$$$ decomposed into its spatially dependent weights and basis functions, see Eq. (1). Accordingly, image reconstruction is performed in x-pc space (corresponding Fourier and PCA transformations $$$F_{b->f}$$$ and $$$B_{f->pc}$$$).

$$arg min_{\vec{i}} \|E\vec{i}-\vec{d}\|_{2}^{2} + \lambda\|^{x-pc}M^{-1}B_{f->pc}F_{b->f}\vec{i}\|_{2}^{2} \qquad(1)$$

Using a segmented least-squares fit as described in [9], IVIM parameter maps were derived. Data from 11 healthy volunteers (3 males, 8 females, age: 27+/-4 years) was obtained using a 3T Philips Achieva scanner (Philips Healthcare, Best, the Netherlands) equipped with an 8-channel head coil. Imaging parameters were: single-shot 2D EPI with 181 lines, field-of-view 218x180x65 mm³, partial Fourier factor 0.65, 9 slices, slice gap 2.5 mm, voxel size 1.2x1.2x5 mm³, TE=81 ms, TR=4 s, 8 averages, 6 gradient optimized diffusion directions with 16 b-values between 0-900 s/mm² [2,3]. Total scan time was 24 min 24 s for the fully sampled data.

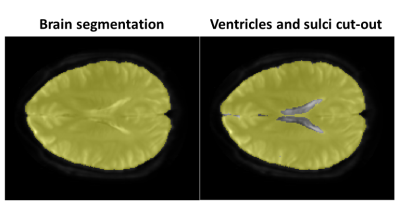
Reconstruction errors were investigated for parallel imaging (iterative SENSE using conjugate gradients [10]) and the two proposed methods k-b PCA and k-b_pp PCA (regularization parameter λ=10^-4, number of training profiles N_train=9) considering various undersampling factors. For error analysis, the brain was segmented using active contours [11]. The ventricles, sulci and other CSF rich areas were cut out from the region-of-interest (ROI) thereafter by performing an IVIM fit to the fully sampled reference (Ref.) and excluding voxels with D≥2·10^-3 mm²/s and f≥30% as shown in Figure 2.

Results

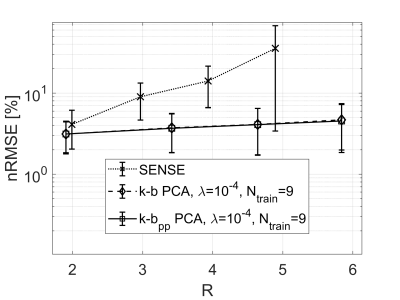
Reconstructed magnitude images using SENSE exhibit visible undersampling artifacts and noise amplification for R≥2, while the proposed methods significantly reduce artifact levels (Figure 3). The mean and standard deviation (Figure 4) across all volunteers and slices of the reconstruction error in terms of root mean squared error (RMSE) normalized to the root mean squared magnitude of the fully sampled reference (nRMSE), averaged across the individual ROIs are for SENSE: 4.1±2.1% (R=2.0) up to 35.6±32.2% (R=4.9) and 3.1±1.3/3.1±1.4% (R=1.9) up to 4.7±2.7/4.5±2.7% (R=5.8) for k-b PCA/ k-b_pp PCA.

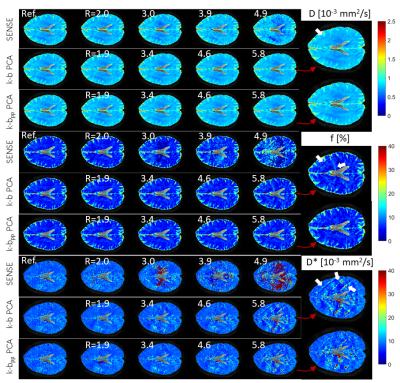
The IVIM parameter estimates in Figure 5 show artifacts for R≥3 in all three IVIM parameters, while the k-b PCA derived parameters remain nearly artifact free up to R=4.6. With k-b_pp PCA, parameters D and f do not exhibit visible artifacts up to R=5.8. The IVIM parameter estimation errors are provided as RMSE averaged across the ROIs in Figure 6. Mean and standard deviation across all datasets for the maximum undersampling factor tested are summarized in Table 1.

Discussion and Conclusion

Acknowledgements

References

1. Le Bihan D. Intravoxel incoherent motion imaging using steady-state free precession. Magn. Reson. Med. 1988;7:346–351.

2. Federau C, Maeder P, O’Brien K, Browaeys P, Meuli R, Hagmann P. Quantitative measurement of brain perfusion with intravoxel incoherent motion MR imaging. Radiology 2012;265:874–81. doi: 10.1148/radiol.12120584.

3. Federau C, O’Brien K, Meuli R, Hagmann P, Maeder P. Measuring brain perfusion with intravoxel incoherent motion (IVIM): initial clinical experience. J. Magn. Reson. Imaging 2014;39:624–632. doi: 10.1002/jmri.24195.

4. Ohliger MA, Grant AK, Sodickson DK. Ultimate Intrinsic Signal-to-Noise Ratio for Parallel MRI: Electromagnetic Field Considerations. Magn. Reson. Med. 2003;50:1018–1030. doi: 10.1002/mrm.10597.

5. Wiesinger F, Boesiger P, Pruessmann KP. Electrodynamics and ultimate SNR in parallel MR imaging. Magn. Reson. Med. 2004;52:376–390. doi: 10.1002/mrm.20183.

6. Pedersen H, Kozerke S, Ringgaard S, Nehrke K, Won YK. K-t PCA: Temporally constrained k-t BLAST reconstruction using principal component analysis. Magn. Reson. Med. 2009;62:706–716. doi: 10.1002/mrm.22052.

7. Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer F a. Fast MR parameter mapping using k-t principal component analysis. Magn. Reson. Med. 2011;66:706–16. doi: 10.1002/mrm.22826.

8. Schmidt JFM, Wissmann L, Manka R, Kozerke S. Iterative k-t principal component analysis with nonrigid motion correction for dynamic three-dimensional cardiac perfusion imaging. Magn. Reson. Med. 2014;72:68–79. doi: 10.1002/mrm.24894.

9. Spinner GR, von Deuster C, Tezcan KC, Stoeck CT, Kozerke S. Bayesian intravoxel incoherent motion parameter mapping in the human heart. J. Cardiovasc. Magn. Reson. 2017;19:85. doi: 10.1186/s12968-017-0391-1.

10. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn. Reson. Med. 2001;46:638–651. doi: 10.1002/mrm.1241.

11. Chan TF, Vese L a. Active contours without edges. IEEE Trans. Image Process. 2001;10:266–277. doi: 10.1109/83.902291.