5339
Novel Image-based Nyquist Ghost Correction of Diffusion-Weighted Echo Planar Imaging using Ghost/Object Minimization1Biomedical Engineering, University of Minnesota, Minneapolis, MN, United States, 2Department of Radiology, University of Minnesota, Minneapolis, MN, United States, 3Department of Pediatrics, University of Minnesota, Minneapolis, MN, United States
Synopsis
Diffusion weighted imaging (DWI) acquired with SE-EPI is subject to Nyquist ghosts, which are commonly corrected using a three-line navigator. However, several alternative ghost correction strategies do not require any reference acquisition. These methods define a cost function that is minimized when the image is ghost-free. We propose a novel referenceless method called ghost/object minimization by defining the cost function as the summation over the image divided by its ½-FOV-shifted counterpart. In this work, we test noise sensitivity and demonstrate the feasibility of the ghost/object minimization using simulated ghosts and in vivo acquisitions including brain, prostate, breast, and liver DWI.
Introduction
Diffusion weighted imaging (DWI) acquired with single shot spin-echo echo-planar imaging (SE-EPI) is subject to Nyquist (or N/2) ghosts caused by eddy currents, imperfect gradients, and/or timing errors. An image with a typical first order ghost is described by: $$M(x,y)=M_0 \left(x,y\right) \cos\left(2πκx+ϕ\right)+iM_0 \left(x,y-\frac{FOV}{2}\right) \sin\left(2πκx+ϕ\right)$$ where M0 is the ideal image and κ and φ correspond to the 1st and 0th order phase differences between alternating lines in ky-x-space. Nyquist ghosts are commonly corrected using a 3-line navigator to measure the phase difference1. However, several alternative ghost correction strategies do not require any navigator acquisition, which may allow for shorter TE. These methods work by defining a cost function fcost(κ,ϕ) which is minimized when the image is ghost-free. Examples include the entropy method2,3, which minimizes the entropy in the image domain, and the SVD method4, which operates on k-space. The performance of these methods is generally good but it can vary with geometry, signal to noise ratio (SNR), and amount of ghost-object overlap.
In this work we introduce a new referenceless method called Ghost/Object minimization (G/O). We define the cost function as the summation over the image divided by a ½-FOV-shifted version of the image: $$$\sum_{x,y}^{}\frac{M\left(x,y-\frac{FOV}{2}\right)}{M(x,y)}$$$. In this work, we test the sensitivity to noise and demonstrate the feasibility of this technique in several applications using DW SE-EPI.
Methods
Simulation
A Shepp-Logan phantom with complex noise was simulated with a realistic ghost by adding a phase ramp to alternating lines in the ky-x domain (κ=-0.42, ϕ=-0.15). The three methods were tested by calculating each fcost over a discrete parameter space (κ, ϕ), locating the minimum, and applying the correction (κmin, ϕmin) to the image. The experiment was repeated with randomly varying ghost parameters and increasing noise (10 noise levels, 100 trials per level) to assess SNR sensitivity.
In vivo
To demonstrate in vivo feasibility, each referenceless method was retrospectively applied to DWI acquired in several body regions. Corrections were made independently for each channel, slice, and repetition for 1) brain DWI with simultaneous multi-slice (SMS, MB=4), 2) breast DWI with GRAPPA (R=2), 3) fully-sampled prostate DWI, and 4) liver DWI with R=3 and segmented ACS lines. For parallel imaging cases, the initial ghost correction was estimated using the auto calibration scans (ACS) and applied to the undersampled data. Ghost correction was then refined on a per-channel and per-repetition basis after GRAPPA reconstruction. Apparent diffusion coefficient (ADC) maps were generated using a pixel-by-pixel log-linear fit.
Results
Figure 1 shows the cost functions measured on the simulated dataset. The bottom row demonstrates the image before correction, after correction by an incorrect solution that corresponds to a local minimum of SVD, and with the correct solution, i.e. the global minima of all metrics. The error as a function of noise level is plotted in Figure 2; the G/O method appears to be less sensitive to noise than Entropy or SVD.
Brain data acquired with SMS (MB=4) b=0 s/mm2 images are shown in Figure 3 as a montage across all slices and a close-up of a subset, scaled to highlight residual ghosts. The online reconstruction fails to fully correct the ghosts in this case, while all three referenceless methods achieve almost complete ghost suppression.
Fully reconstructed axial ADC maps are shown in Figures 4 and 5 from the breast, prostate, and liver DWI. In this breast case, both SVD and G/O eliminate the ghost, however there is a small residual ghost visible after the entropy correction. SVD performed poorly in all slices of this prostate case, while both entropy and ghost ratio fully suppressed the ghost. In the selected slice of liver DWI, SVD performs best, which is consistent for most but not all of the other slices.
Discussion
We have demonstrated the feasibility of ghost correction with ghost/object minimization in a variety of DWI data. A careful comparison of G/O with the linear navigator and other referenceless methods was performed in breast R=3 data5, but further work is needed to compare in prostate, liver, and brain imaging. Although background regions were assessed visually as a surrogate for ghost correction performance, even inconspicuous residual ghosts can bias diffusion parameters in the tissue.
In general, entropy and SVD methods work well, but in some cases one performs noticeably worse. The addition of G/O provides a third independent option, which can be combined with entropy and SVD for increased robustness5.
Conclusions
Ghost correction by G/O is feasible in DWI of both brain and body applications. The cost function of G/O has different characteristics than the other referenceless methods and may be less sensitive to noise.Acknowledgements
NIH P41 EB015894
NIH R21 CA201834
UMN Medical School Foundation
NIH/NIDDK R01 DK105953
References
- Heid, O. (2000). Method for the phase correction of nuclear magnetic resonance signals.
- Clare, S. (2003). Iterative Nyquist ghost correction for single and multi-shot EPI using an entropy measure. In Proceedings of the 16th Annual Meeting of ISMRM, Toronto, Canada, p. 1041.
- Skare, S., Clayton, D.B., Newbould, R., Moseley, M., and Bammer, R. (2006). A fast and robust minimum entropy based non-interactive Nyquist ghost correction algorithm. In Proc. Intl. Soc. Mag. Reson. Med, (Seattle, Washington), p. 2349.
- Peterson, E., Aksoy, M., Maclaren, J., and Bammer, R. (2015). Acquisition-free Nyquist ghost correction for parallel imaging accelerated EPI. In Proc. Intl. Soc. Mag. Reson. Med., (Toronto, Ontario), p. 0075.
- McKay JA, Moeller S, Zhang L, Auerbach EJ, Nelson MT, Bolan, PJ. (2017) Comparison of Referenceless Methods for EPI Ghost Correction in Breast Diffusion Weighted Imaging. In Proceedings of the 26th Annual Meeting of ISMRM [Submitted]
Figures
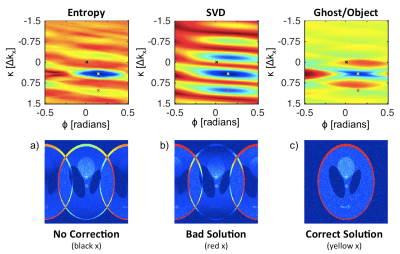
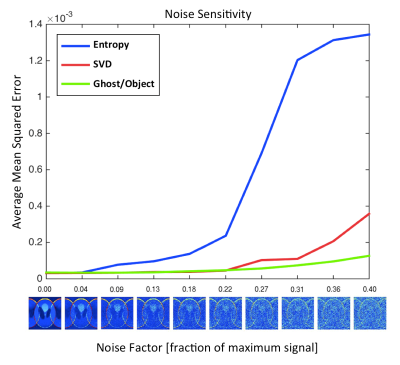
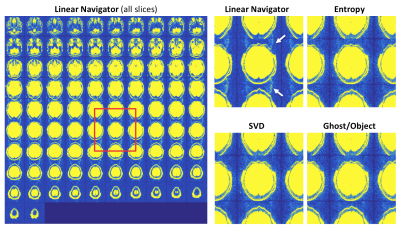
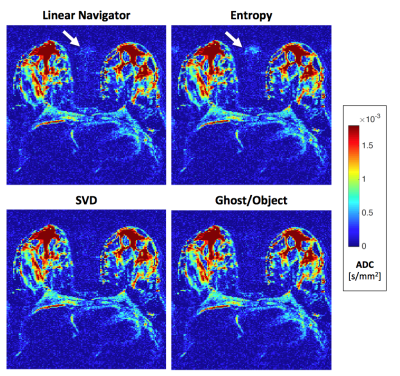
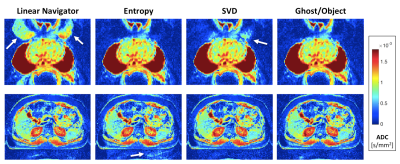
Figure 5. Axial ADC maps. Top: fully-sampled prostate DWI acquired on Siemens 7 T Magnetom at b = 0 and 1000 s/mm2. Bottom: undersampled (R = 3) liver DWI with segmented ACS lines (3 segments, EPI) acquired on Siemens 3 T Prismafit at b = 0, 50, 400, and 800 s/mm2 . The standard navigator correction clearly fails (white arrow), and SVD leaves residual ghosts (white arrow) in nearly all of the slices of the prostate images. The ghost correction performance of all the methods is quite variable in the liver data. PE direction is anterior-posterior in both cases.