5332
Multi-Shot Diffusion-Weighted EPI Reconstruction Based on Locally Low-Rank Constraints1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong SAR, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong SAR, China
Synopsis
Based on the locally low rank (LLR) property of multi-shot diffusion-weighted imaging (DWI), a novel reconstruction scheme is proposed to achieve high signal-to-noise ratio (SNR) without explicit estimation of inter-shot phase variation. The results from in vivo DWI data indicate that the proposed method can effectively improve the image quality at various shot numbers when compared with traditional shot-by-shot reconstruction approaches.
Introduction
Diffusion-weighted imaging (DWI) is a widely-used non-invasive technique to investigate the microstructure of tissues in vivo. Single-shot parallel DWI acquisition has immunity to bulk motion but sometimes fails to provide satisfying images due to its inherent limitations, e.g., large geometric distortion and blurring artifacts1. These limitations can be alleviated by multi-shot techniques which are particularly suitable for high resolution imaging. One main challenge of multi-shot DWI reconstruction is the inter-shot phase variation induced by subpixel motions of samples. Traditional multi-shot DWI reconstruction methods employ shot-by-shot reconstruction with magnitude average, which often cause considerable signal-to-noise ratio (SNR) loss due to g-factors during parallel imaging reconstruction2,3. Some recent methods explicitly estimate the inter-shot phase variation, which can be, however, unreliable in some cases, e.g. when individual shots are highly undersampled4. Low-rank constraints exist in multi-shot data due to the smoothness of inter-shot phase variation. In this study, we propose to use locally low-rank (LLR) constraints combined with eigenvector-based iterative self-consistent parallel imaging reconstruction (ESPIRiT) to reconstruct multi-shot DWI data. This approach requires no estimation of inter-shot phase variation and can reliably offer high-SNR images at various shot numbers.Methods
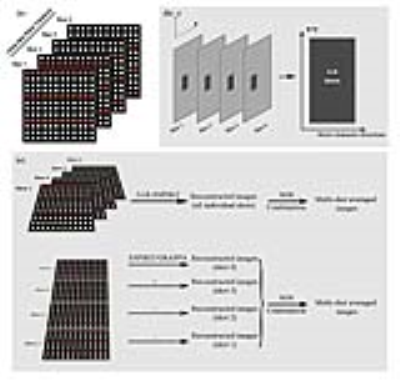
Procedure: Due to the inter-shot phase variation, diffusion-weighted data acquired from individual shots cannot be directly combined (Fig. 1-a). The proposed method reformats the multi-shot data matrices into a Casaroti matrix, where small spatial patches form the rows and other dimensions (i.e. shots, channels and directions) form the columns (Fig. 1-b). This Casaroti matrix is inherently low-rank, because the inter-shot phase variation is spatially smooth4. ESPIRiT, which is an extension of SENSE with 2 sets of coil sensitivity maps from eigenvalue analysis, is then combined with the above LLR constraints (LLR-ESPIRiT) using The Berkeley Advanced Reconstruction Toolbox (BART)5,6.
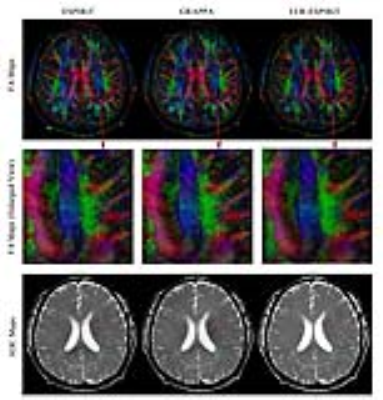
Experiments: In-vivo human brain EPI-based diffusion data sets were acquired on a 1.5T MR scanner using an 8-channel head coil with 2, 3, and 4 shots, respectively. The imaging parameters were TR/TE=4000/37ms, single diffusion direction, single average and b-value=1000. LLR-ESPIRiT and shot-by-shot ESPIRiT were implemented by using BART Toolbox in MATLAB environment with L2-norm regularization factor of 0.015 (for both LLR- and shot-by-shot ESPIRiT) and LLR regularization factor of 0.0015 (for LLR-ESPIRiT). The ESPIRiT coil sensitivity maps were calculated from b=0 EPI, which was 1D linear phase corrected and processed by virtual coil based simultaneous auto-calibrating and k-space estimation (VC-SAKE) to fully remove Nyquist ghosts. Shot-by-shot GRAPPA with regularization factor of 0.01 was also implemented in MATLAB for comparison. Monte-Carlo SNR maps were calculated by using pseudo replica method7. In addition, a set of DTI data (3-shot, 6 diffusion directions, single average, b-value=800) were acquired and reconstructed, from which fractional anisotropy (FA) and apparent diffuse coefficient (ADC) maps were calculated using Diffusion Toolkit. The inconsistent geometric distortions in different diffusion directions were removed by affine co-registration in MATLAB before DTI analysis.
Results
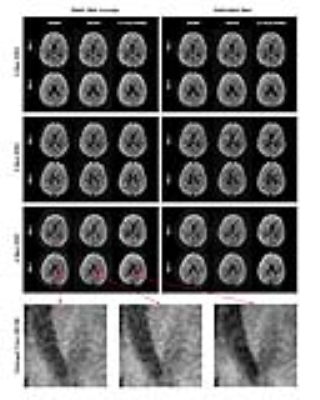
Fig. 2 shows that compared to shot-by-shot GRAPPA or ESPIRiT, the images reconstructed by the proposed method had higher SNR, especially when the shot number was large.
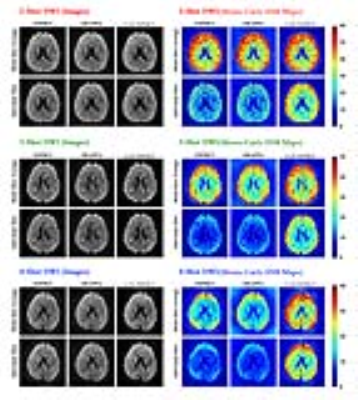
Fig. 3 further demonstrates the SNR improvement using the Monte-Carlo SNR maps. The proposed method led to obviously increased SNR for 3- and 4-shot datasets. Due to the LLR contraints among shots, the improvement on the individual-shot images were even more dramatic than that on multi-shot averaged images.
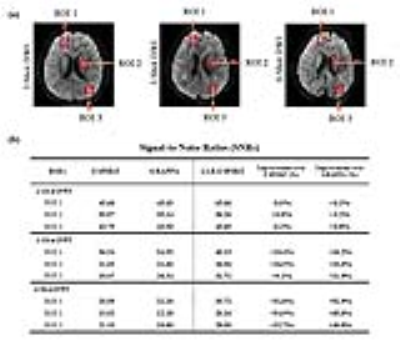
Fig. 4 provides quantitative assessments of the SNR in three regions of interest (ROIs). SNRs by the proposed method were improved in all ROIs. For 3- and 4-shot data, the improvement was 10%-20% and 30% to 50%, respectively.
Fig. 5 shows that the proposed method could reduce the noise and aritfacts in the FA and ADC maps.
Discussion and Conclusion
We have demonstrated that the proposed method using LLR ESPIRiT can effectively improve the SNR of multi-shot diffusion-weighted images when compared with traditional shot-by-shot approaches. When the number of shots increases, LLR-ESPIRiT shows more apparent SNR advantages. Another potential advantage of the proposed method is that it can offer high-SNR individual-shot images, which may benefit co-registration of different diffusion directions. Furthermore, the 6-direction DTI dataset were successfully reconstructed with data from all diffusion directions organized into one low-rank matrix. This suggests that the LLR-ESPIRiT method can handle not only inter-shot phase variation, but also slight geometric distortion. In conclusion, the proposed LLR-ESPIRiT method can be a robust method to achieve high-SNR reconstruction for multi-shot diffusion-weighted imaging.Acknowledgements
This work was supported by the Hong Kong Research Grant Council (Grants C7048-16G and HKU17103015 to E.X.W.).References
1. Jeong, H. K., et al. (2013). High‐resolution human diffusion tensor imaging using 2‐D navigated multishot SENSE EPI at 7 T. Magnetic resonance in medicine, 69(3), 793-802.
2. Pruessmann, K. P., et al. (1999). SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine, 42(5), 952-962.
3. Griswold, M. A., et al. (2002). Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic resonance in medicine, 47(6), 1202-1210.
4. Mani, M., et al. (2017). Multi‐shot sensitivity‐encoded diffusion data recovery using structured low‐rank matrix completion (MUSSELS). Magnetic resonance in medicine, 78(2), 494-507.
5. Uecker, M., et al. (2014). ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine, 71(3), 990-1001.
6. Zhang, T., et al. (2015). Fast pediatric 3D free‐breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution. Journal of Magnetic Resonance Imaging, 41(2), 460-473.
7. Robson, P. M., et al. (2008). Comprehensive quantification of signal‐to‐noise ratio and g‐factor for image‐based and k‐space‐based parallel imaging reconstructions. Magnetic resonance in medicine, 60(4), 895-907.
Figures