5326

Highly efficient diffusion MRI by Slice-interleaved Free-waveform Imaging (SIFI)

Jana Hutter¹, Markus Nilsson², Daan Christiaens¹, Torben Schneider³, Anthony N Price¹, Joseph V Hajnal¹, and Filip Szczepankiewicz^2,4

¹Biomedical Engineering, King's College London, London, United Kingdom, ²Clinical Sciences, Lund University, Lund, Sweden, ³Philips Healthcare, Guilford, United Kingdom, ⁴Random Walk Imaging AB, Lund, Sweden

Synopsis

Diffusion encoding along multiple directions in a single shot facilitates probing of tissue microstructure that is not accessible with conventional (linear) tensor encoding. However, it tends to engage gradients on multiple axes in a pattern that yields higher energy consumption, which can become a critical limiting factor for gradient system performance. Here, we show that Slice Interleaved Free-waveform Imaging (SIFI) of b-tensor size, orientation, and shape reduces peak power consumption and heating, which translates to markedly reduced repetition time, shorter examination times and higher temporal SNR.

Introduction

B-tensor encoding was recently proposed^1-2 as a novel framework for diffusion weighted imaging. It enables a novel dimension by expanding the shape of the diffusion encoding tensor beyond conventional linear tensor encoding (LTE) e.g. by including spherical-tensor-encoding (STE)³. The generated data allows sources of heterogeneity to be disentangled – yielding exciting results¹. Technically, the encoding uses free-waveform gradients, yielding specific q-space trajectories. Optimized waveforms^5,7 are required for feasible echo times; waveforms with the highest efficiency leverage the full capacity of the hardware (maximal gradient strength/slew). This operating mode puts strain on the gradients and can result in inflated scan times due to excessive power consumption and ohmic heating. While a b-tensor encoding protocol with feasible scan times was demonstrated recently⁶, any decrease in the acquisition time would benefit wider usage. So far, acquisition of different tensor shapes was performed in separate scans, but this complicates its use and increases the risk for inconsistent data – specifically in applications prone to motion and scan interruption. This novel sequence version allows Slice-Interleaved-Free-waveform Imaging (SIFI) providing complete freedom in the choice of the size, orientation, and shape of the encoding on a slice-by-slice level. Beyond the immediate benefits of reduced scan time and higher internal data consistency, the increased temporal sampling of low-b slices might improve outlier rejection, motion and distortion correction⁸ – all facilitating b-tensor encoding in motion-rich applications.

Methods

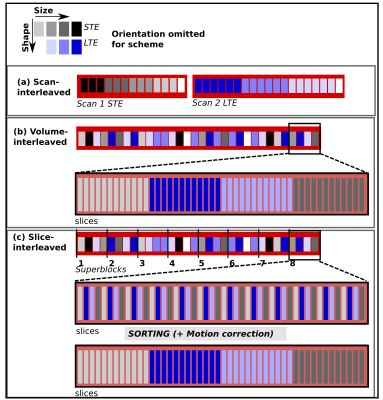
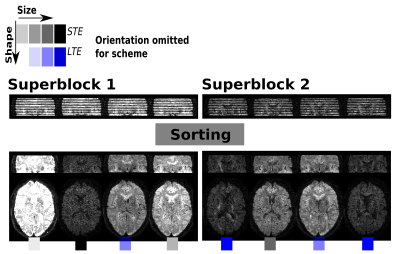
Currently, the high demand from sustained gradient-intense volumes – requiring the same encoding for every slice – leads to power and heating peaks. Although they make up only a small fraction of the required volumes, they set the required gradient cooling time and thus extend the repetition time for the entire scan. SIFI breaks with two of the mentioned conventions to address this challenge: The original free-waveform sequence1,5 (scan-interleaved) was modified (I) to allow dynamic switching between waveforms within one scan (volume-interleaved), and (II) to break with the traditional “one-volume one-encoding” paradigm⁸. These changes were implemented into the EPI sequence on a clinical 3T Philips Achieva scanner to allow complete freedom in the choice of size, orientation and shape of the encoding tensor for every slice (slice-interleaved). Fig.1 illustrates both the volume-interleaved version as well as slice-interleaved version on a 12-slice stack. To ensure usable datasets even in interrupted acquisitions, we introduce the concept of super-blocks – each made up from N volumes, containing slices from N encodings⁹. The whole acquisition is composed of multiple super-blocks. To maximally spread the demands on the gradient system, each super-block consists of interleaved high/low-demand waveforms (typically STE/LTE, Fig.1). The interleaving reduces peak demand to a level within the available supply of power and cooling. The obtained data can be sorted to the traditional volume order. Alternatively, the quick temporal encoding variations can be used to facilitate motion correction for highly attenuated SNR poor higher-b slices₈. The parameters of the slice-interleaved version were: two b=0, and b=[100,500,1000,1800]s/mm² in three/six directions for STE/LTE respectively; FOV=240x240mm2, 28 slices, resolution=2mm³, TE=100ms, SENSE2, partial-Fourier=0.8, Gmax/slew=78mT/s, 100mT/m/s, pre180post180=38.9ms/29.4ms. The optimized⁵ STE waveform was Maxwell-compensated⁷, the LTE waveform chosen to maximize encoding efficiency (Fig.2).

Results and Discussion

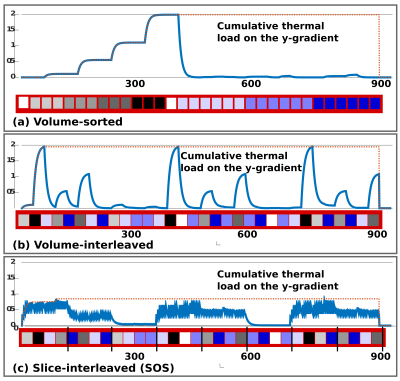
SIFI data was acquired on a healthy volunteer on a clinical Philips 3T-Achieva at high Gmax without requiring TR-extension and without producing any peripheral-nerve-stimulation (PNS). The pilot testing was conservative as thermal load and PNS modelling are not yet completely automated. The initial thermal load simulations depicted in Fig. 3 for volume-sorted, volume-interleaved and slice-interleaved versions represent only the thermal demands based on a basic vendor load model⁸. However, it shows the large achievable reduction in system demand. For the chosen example and assuming the LTE waveform on all three axis for STE-encoding to allow standard vendor sequence validation, the time with volume-interleaving was reduced by factor 1.9. This is a conservative estimate since our load modelling indicates that STE presents higher demands than LTE. The resulting SIFI data is depicted before and after sorting in Fig.4, illustrating that conventional volumes could be obtained.

Conclusion and Outlook

Slice-level interleaving of diffusion encodings is especially beneficial for gradient waveforms operating at the hardware limit – such as in b-tensor encoding.⁵ Interleaved encoding can reduce the scan time significantly. The reduction depends largely on the chosen parameters, in the given example with moderate b-value and only 28 slices the conservatively estimated achieved reduction was 1.9. This can be translated to higher angular resolution, or denser shell sampling. Further work will involve the optimized automatic ordering of the encodings while respecting all constrains (power, cooling and PNS). The implementation further allows slice-level¹⁰ adaption of the phase-encoding-direction – expected to improve distortion correction – as well as slice excitation order – allowing simultaneous T1-diffusion mapping¹¹.

Acknowledgements

This work received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/20072013)/ERC grant agreement no. 319456 (dHCP project), the NIH Human Placenta Project grant 1U01HD087202-01, the Wellcome Trust (Sir Henry Wellcome Fellowship, 201374/Z/16/Z) and was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1 and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.

References

[1] F. Szczepankiewicz, S. Lasic, D. van Westen, P. Sundegren, E. Englund, C-F. Westin, F. Stahlberg, J. Laett, D. Topgaard, M. Nilsson, “Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors”, Neuroimage 104 (2015), 241-252

[2] Westin, C.-F., Knutsson, H., Pasternak, O., Szczepankiewicz, F., Ozarslan, E., van Westen, D., et al. (2016). Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage, 135(C), 345–362. http://doi.org/10.1016/j.neuroimage.2016.02.039

[3] Eriksson, S., Lasič, S., & Topgaard, D. (2013). Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. Journal of Magnetic Resonance (San Diego, Calif : 1997), 226, 13–18. http://doi.org/10.1016/j.jmr.2012.10.015

[4] Lasič, S., Szczepankiewicz, F., Eriksson, S., Nilsson, M. & Topgaard, D. 2014. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2, 11

[5] J. Sjolund, F. Szczepankiewicz, M. Nilsson, D. Topgaard, C-F. Westin, H. Knutsson, “Constrained optimization of gradient waveforms for generalized diffusion encoding”, JMR 261 (2015), 157-168

[6] Szczepankiewicz, F., Sjölund, J., Ståhlberg, F., Lätt, J. & Nilsson, M. 2016. Whole-brain diffusional variance decomposition (DIVIDE): Demonstration of technical feasibility at clinical MRI systems. arXiv:1612.06741

[7] Szczepankiewicz, F. and Nilsson, M. 2018. Maxwell-compensated waveform design for asymmetric diffusion encoding. Submitted to Int. Soc. Magn. Reson. Med. Paris, France.

[8] Hutter, J., Christiaens, D., Kuklisova-Murgasova, M., Cordero-Grande, L., Slator, P., Price, A., Rutherford, M., Hajnal, J. V , “Dynamic field mapping and motion correction using interleaved double spin-echo diffusion MRI” 1 Oct 2017, Lecture Notes in Computer Science - MICCAI 2017, Vol. 10433 LNCS, 523-531

[9] Cook, PA, Symms, M, Boulby, PA & Alexander, D. C. 2007. Optimal acquisition orders of diffusion-weighted MRI measurements. Journal of Magnetic Resonance Imaging, 25, 1051-8.

[10] Hutter J, Tournier, D., Price, A., Cordero-Grande, L., Hughes, EJ., Malik, S., Steinweg, J., Bastiani, M., Sotiropoulos, S., Andersson, J., Edwards, D., Hajnal, JV, “Time-efficient and flexible design of optimized multishell HARDI diffusion”, Magnetic Resonance in Medicine 2017, in-press

[11] Hua Wu, Qiyuan Tian, Christian Poetter, Kangrong Zhu, Matthew J Middione, Adam B Kerr, Jennifer A McNab, and Robert F Doughert, Whole Brain Inversion Recovery Diffusion Weighted Imaging Using Slice-Shuffled Acquisition ISMRM 2017, 0387

Figures

Fig.1: Schematic illustration of the scan-interleaved, volume-interleaved and slice-interleaved versions. Thereby only the size and the shape of the encoding are illustrated by color, the orientations were omitted for simplicity in this representation.

Fig.2: Diffusion encoding gradient waveforms that were used for all acquired datasets and simulations. The two periods, separated by zero gradients, are waveforms played out before and after the refocusing pulse. Spherical and linear b-tensor encoding (STE and LTE) are shown in the left and right panels, respectively.

Fig.3: Thermal load evolution over slices for volume-sorted, volume-interleaved and slice-interleaved cases.

Fig. 4: The first block of an SIFI dataset acquired with the described protocol before and after sorting (top and bottom rows) in coronal and transverse view.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5326