5250

Axonal distributions: a simulation study to estimate Diffusion MRI signal contributions in white matter
Andrea Chiappiniello1, Valentina Reggioli2, Roberto Tarducci2, Marco Catani3, and Flavio Dell’Acqua3

1Physics and Geology Department, University of Perugia, Perugia, Italy, 2Medical Physics Department, Santa Maria della Misericordia Hospital, Perugia, Italy, 3NATBRAINLAB, Institute of Psychiatry, Psychology and Neuroscience, King’s College London, London, United Kingdom

Synopsis

In the last decade, many techniques that use diffusion MRI to obtain an axon diameter estimate as micro-structural integrity index have been developed. However, recent studies showed that diffusion signal may be not sensitive enough to quantify axon diameters. In this study, we simulated a simplified model of white matter to evaluate the contribution of intra-axonal compartment to diffusion MRI signal in white matter. We found that, even in distributions with a small mean diameter, big axons still substantially contribute to the total axonal volume. We conclude that quantifications of human axon diameters from diffusion MRI may still be possible.

Introduction

Axonal diameter and density are important features of axon morphology and play an important role in neuronal functions. Axon diameters vary between 0.2 and 20 μm and provide information about function and performance of white matter pathways.1 It is well known that conduction velocity is proportional to axon diameter.2,3 On the other hand, thin axons can be more densely distributed, allowing to carry large volume of information despite transmission speed.4,5 Over the last years, a number of techniques6,7 that use information of tissue micro-structure provided by diffusion MRI have been implemented to obtain an axon diameter index. However, more recent studies have highlighted that diffusion signal acquired by existing MR scanners may be not sensitive enough to quantify axon diameter in realistic biological ranges.8-10 Indeed, sensitivity to axons with small diameter is limited by scanner gradient strength and type of pulse sequence.8 Moreover, time-dependent diffusion MRI signal from extra-axonal water could dominate that of intra-axonal water, employing clinical diffusion gradients.9,10 These elements could explain the axon diameters overestimation7 assessed by current techniques. However, another explanation for this overestimation is that the signal contribution from large axons is substantially dominating over the more numerous but smaller axons. The aim of this study is to estimate and reevaluate by simulations the actual signal contributions within the intra-axonal compartment when realistic distributions of axonal diameters are considered.

Materials and methods

2D simulations of transversal sections of parallel cylindrical axons were performed using MATLAB. Axon diameters between 0.3 and 12 µm were simulated. A myelin layer around the axons was considered using a g-ratio (i.e. the ratio between axon diameter and fiber diameter) of 0.7. This value is considered to be optimal for signal conduction11 and has already been adopted in previous studies12-14. From the histology data reported by Aboitiz et al., 1992, a ≈70% mean fiber density was estimated in the whole human corpus callosum (CC) and considered for the simulations. Fibers were positioned in a 0.25x0.25 mm2 box following 1) a uniform distribution and 2) couldn’t overlap each other. Both gamma, gaussian and log-normal distributed diameter were considered, changing each time distribution parameters to get distribution profiles in line with existing literature4. In this study, we have focus on the quantification of the actual volume fraction, and equivalently the signal contribution, coming from the largest axons (>3 µm) even when the mean diameter is <1 µm. These values were chosen to take into account the sensitivity limit of the connectome scanner (Gmax=300 mT/m)8,15. Numerical simulations were run 5 times and results were then averaged. To compare our results with histological data, a review of the literature4,6 was also performed to estimate the volume fraction, or the axonal space, occupied by axons as a function of the mean of their diameter distribution.

Results and Discussion

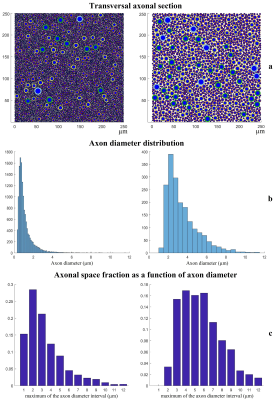
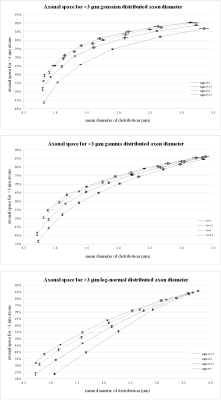
Figure 1a-c shows representative results from two log-normal distributions. The simulated transversal sections are shown in 1a), their axonal distribution histograms in 1b) and axonal space contribution for different fractions of axonal diameters are reported in 1c). Figure 2, shows the fraction of axonal space occupied by axons with diameters >3 µm for different distribution profiles. Although changes in the original distribution affect the final histograms and axonal space organization, a few trends are consistently observed in all simulations:

Thanks to the quadratic relation between axonal section and diameter, few big axons can be responsible for most of the total axonal signal. Even in distributions with mean diameter <1 µm, an important fraction of axonal space is usually occupied by axons with a diameter >3 µm. On the contrary, small axons (<1 µm) contribute marginally to the total axonal signal.

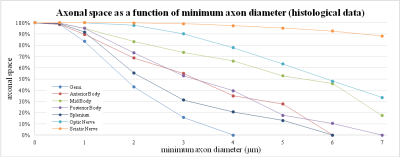
These results are compatible with the same analysis performed on human histological data as shown in figure 3.

Conclusions

In this study, we simulated a simplified model of white matter to better understand the actual signal contribution of different axonal diameters for realistic diameter distributions. Histology data and simulations highlighted an important contribution of big axons to the total signal. If this contribution is enough to explain previously reported overestimations of axonal diameters this is not immediately obvious. Other signal contributions and time dependences9 also need to be considered.

In conclusion, while small axons may be still currently beyond the resolving power of present MR hardware, their contribution to the overall axonal signal also seems to be modest. On the contrary, larger axons even if fewer in number may still generate a non-negligible signal that could be useful to infer microstructure properties of white matter. More studies are required to investigate this possibility.

Acknowledgements

No acknowledgement found.

References

1. Waxman, SG. Determinants of conduction velocity in myelinated nerve fibers. Muscle Nerve, 1980; 3:141–150.

2. Ritchie, JM. On the relation between fibre diameter and conduction velocity in myelinated nerve fibres. Proc R Soc Lond B Biol Sci, 1982; 217:29–35.

3. Waxman SG, Kocsis JD, Stys PK. The axon. Structure, Function and Pathophysiology. Oxford University Press, 1995, New York.

4. Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res., 1992; 598:143–153.

5. Lamantia AS, Rakic P. Cytological and quantitative characteristics of four cerebral commissures in the rhesus monkey. J. Comp. Neurol., 1990; 291:520–537.

6. Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn. Reson. Med., 2008; 59:1347–1354.

7. Alexander DC, Hubbard PL, Hall MG, Moore EA, Ptito M, Parker GJM, Dyrby TB. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage, 2010; 52:1–16.

8. Drobnjak I, Zhang H, Ianuş A, Kaden E, Alexander DC. PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magn. Reson. Med., 2016; 75(2):688–700.

9. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc. Natl. Acad. Sci., 2014; 111:5088–5093.

10. Burcaw LM, Fieremans E, Novikov DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. Neuroimage, 2015; 114:18–37.

11. Rushton WAH. A theory of the effects of fibre size in medullated nerve. J. Physiol., 1951; 115:101–122.

12. Pajevic S, Basser PJ. An optimum principle predicts the distribution of axon diameters in normal white matter. PLoS One, 2013; 8, e54095+.

13. Sepehrband F, Clark KA, Ullmann JFP, Kurniawan ND, Leanage G, Reutens DC, Yang Z. Brain tissue compartment density estimated using diffusion-weighted MRI yields tissue parameters consistent with histology. Hum. Brain Mapp., 2015; 36:3687–3702.

14. Stikov N, Campbell JS, Stroh T, Lavelee M, Frey S, Novek J, Nuara S, Ho MK, Bedell BJ, Dougherty RF, Leppert IR, Boudreau M, Narayanan S, Duval T, Cohen-Adad J, Picard PA, Gasecka A, Cote D, Pike GB. In vivo histology of the myelin g-ratio with magnetic resonance imaging. NeuroImage, 2015; 118:397–405.

15. McNab JA, Edlow BL, Witzel T, Huang SY, Bhat H, Heberlein K, Feiweier T, Liu K, Keil B, Cohen-Adad J, Tisdall MD, Folkerth RD, Kinney HC, Wald LL. The human connectome project and beyond: initial applications of 300 mT/m gradients. Neuroimage, 2013; 80:234–245.

Figures

Figure 1. a) Transversal axonal section from two simulations, selecting the log-normal distribution. Axons are colored in blue, while myelin sheaths have different colors according to axon diameter: black if <2 µm, red if in the range [2:4] µm, orange [4:6] µm, yellow [6:8] µm, green [8:10] µm and light blue if ≥10 µm. b) Histograms of the axon diameter distributions for the simulations in a). c) Axonal space fraction as a function of axon diameter for the distributions in b). X-axis labels express the maximum m of the axon diameter interval ([m-1:m] µm) that was considered for each bin.

Figure 2. Axonal space percentage occupied by axons with a diameter greater than 3 µm for: gaussian (top), gamma (middle) and log-normal (bottom) distributed axon diameters in input. The data were reported by varying mean axon diameter in output and standard deviation (first and third figure) or scale parameter b (second figure) in input. Each value is the average of 5 simulation results.

Figure 3. Axonal space percentage occupied by axons as a function of the minimum axon diameter taken into account. The optic and sciatic nerve data were extrapolated from the histological findings of Assaf et al., 2008, while the others are the CC evaluations from the study of Aboitiz et al., 1992. CC data weren’t corrected for the shrinkage factor (≈1.5) to remain in the worst condition.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
5250