5245
Assessing feasibility and reproducibility of a bundle-specific framework on in vivo axon diameter estimates at 300mT/m1Signal Processing Laboratory 5 (LTS5), Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 2Cardiff University Brain Research Imaging Centre (CUBRIC), Cardiff University, Cardiff, United Kingdom, 3Sherbrooke Connectivity Imaging Laboratory (SCIL), University of Sherbrooke, Sherbrooke, QC, Canada, 4Sherbrooke Molecular Imaging Center, Department of Nuclear Medicine and Radiobiology, Faculty of Medicine and Health Science, University of Sherbrooke, Sherbrooke, QC, Canada, 5Department of Neuroscience, Karolinska Institutet, Stockholm, Sweden, 6Brain and Mind Institute, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 7University Hospital Center (CHUV) and University of Lausanne, Lausanne, Switzerland, 8Department of Computer Science, University of Verona, Verona, Italy
Synopsis
In vivo quantitative estimation of axon diameter in the white matter is a potential new tool for studying the structural and functional architecture of the brain. Recently, the feasibility of axon diameter estimation with diffusion-weighted MRI (DW-MRI) has been questioned. In this work, we explore the feasibility of bundle-specific axon diameter mapping in the context of a reproducibility study using the Convex Optimization Modeling for Microstructure informed Tractography (COMMIT) framework. Our results show that DW-MRI axon diameter estimatesof the corpus callosum and of the corticospinal tract are comparable to histological reports in previous studies.
Purpose
Functional connectivity, together with quantitative estimation of nerve fiber morphology, has a key role in neuroscience. In particular, non-invasive axon diameter mapping may lead to a better understanding of the underlying brain tissue. DW-MRI is the only non-invasive technique for quantifying brain microstructure in vivo. Despite the potential benefits, DW-MRI has so far gained little interest from the neurology and neuroscience communities due to the complexity and challenging aspect of of obtaining reliable axon diameter estimates from MRI systems. Recently, 3 Tesla systems with 300 mT/m gradient coils have been proposed to probe in vivo tissue microstructure in much finer detail. In this work, we propose to use this MRI system to establish the feasibility of obtaining reproducible tract-specific estimates of axon diameter in the living human brain.Methods
Convex Optimization Modeling for Microstructure informed Tractography1,2 (COMMIT) is a framework to complement tractography with additional microstructural information about the neuronal tissue. To estimate of bundle-specific axon diameter index α' (see Equation 7 in Daducci et al.3) a biophysical model similar to Alexander et al.4 can be considered to characterize the neuronal tissue, accounting for both restricted (intra-axonal) and hindered (extra-axonal) water pools as well as partial volume with isotropic diffusion. The observation model of COMMIT is $$$ y=Ax+\eta$$$, where the dictionary $$$A$$$ represents the multi-compartment model built according to the CylinderZeppelinBall model5, $$$\eta$$$ accounts both for modeling errors and acquisition noise and $$$x$$$ are the contribution of all compartments of the model to explain the diffusion data $$$y$$$. The system is solved as a non-negative least-squares problem: $$$ \operatorname{argmin}_{x \ge 0} ||Ax − y|| _2^2$$$ .
In this work, we generated the dictionary $$$A$$$ accounting for the minimum diameter resolution of the MRI scanner6 of 2μm. Hence, we built the dictionary for the intra-axonal compartment with 9 cylinders with diameters equally-spaced in the range 2−10 μm. The extra-axonal space was modeled with zeppelins having d∥ = 1.7 · 10-3 mm2/s and 4 different values for d⊥, whereas diso = 3.0 · 10-3 mm2/s was set to model partial volumes with CSF.
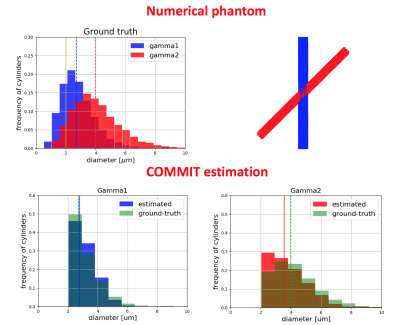
Simulated data. We generated a 45° crossing phantom (Figure 1) consisting of two bundles with gamma distributions having an ADI of 2.7μm and 4.0μm and intra-cellular volume fractions of 0.3 and 0.4, respectively. The extra-cellular signal was computed with an in-house Monte Carlo simulator. Rician noise with SNR=30 was added to the data. The data were simulated for 0.5mm isotropic resolution, 360 DW images distributed on 8 shells and 4 b0, δ=7 ms, G={138, 276, 102, 203, 85, 169, 74, 175} mT/m, Δ={17.3, 17.3, 30, 30, 42, 42, 55, 55}ms.
In vivo data. DW-MRI were acquired for 4 healthy subjects, each repeated 5 times over two weeks using the same protocol as the simulated data with 2mm isotropic resolution and TE = 80ms. DW-MRI were preprocessed for eddy currents7, susceptibility distortion7, motion7 and gradient non linearity. A single T1-weighted image was also acquired, parcellated using FreeSurfer and registered to each DW-MRI dataset. Tractography was performed to obtain 500K streamlines for each dataset using the algorithm iFOD28. We extracted five regions of the Corpus Callosum (CC) and the Corticospinal tract (CST) using the White Matter Query Language9 (WMQL).
Results and discussion
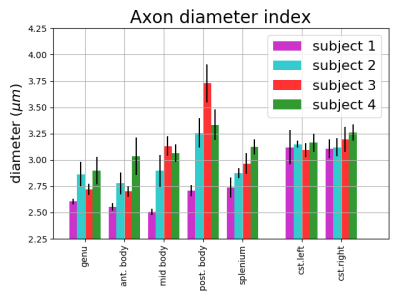
The results of the simulation (Figure 1) show that COMMIT recovers the correct mean diameter of the small bundle (2.7μm) but underestimates the big bundle (4.0μm) by 0.4μm. The results on in vivo data show visual differences among streamlines of the Corona Radiata (Figure 2). We identify a bundle with larger axon diameters for the projections going from precentral and postcentral areas to the brainstem (Figure 3). We report low intra-subject variability in the axon diameter estimation with mean standard deviation of 0.1μm (Figure 3). Furthermore, the trends in the CC from genu to splenium seem to have the expected low-high-low trend as previously shown with histology10,11. We report a low intra-/inter-subject and low left-right coefficient of variation range 0.01-0.05 for the CST.Conclusion
A study on tract-specific diameter mapping was performed to test its feasibility on simulated and in vivo data. We report that COMMIT recovers mean axon diameter estimates close to the simulated ground truth mean diameters. Furthermore, we find that the in vivo results seem closer to the histology than those obtained with voxel-based methods12. We report that subjects have different diameter estimates across the CC sub-bundles, with low variability in the intra-subject analysis. However, the mean axon diameter is high and similar for all subjects for the CST, as reported in histological analysis10,11.Acknowledgements
This project was funded by the Swiss National Fundation, grant 31003A_157063.
The data were acquired at the UK National Facility for In Vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), andThe Wolfson Foundation.
References
1. Daducci A, Dal Palú A, Lemkaddem A and Thiran JP. A convex optimization framework for global tractography. In Proc. IEEE ISBI, pages 524–7, April 2013.
2. Daducci A, Dal Palú A, Lemkaddem A and Thiran JP. COMMIT: Convex Optimization Modeling for Microstructure Informed Tractography. IEEE Trans Med Imaging, 33(1):246–57, 2014.
3. Daducci A, Canales-Rodríguez EJ, Zhang H et al. Microstructure Imaging via Convex Optimization (AMICO) from diffusion MRI data. Neuroimage. 2015 Jan 15;105:32-44
4. Alexander DC, Hubbard PL, Hall MG et al. Orientationally invariant indices of axon diameter and density from diffusion mri. NeuroImage, 52(4):1374–1389, 2010.
5. Panagiotaki E, Schneider T, Siow B et al. Compartment models of the diffusion MR signal in brain white matter: A taxonomy andcomparison. NeuroImage, 59(3):2241–2254, 2012.
6. Nilsson M, Lasič S, Drobnjak I et al. Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR Biomed. 2017 Jul;30(7).
7. Jenkinson M, Beckmann CF, Behrens TE et al. FSL. NeuroImage, 62:782-90, 2012.
8. Tournier J, Clamante F, Connelly A et al. MRtrix: diffusion tractography in crossing fiber regions. Int J Imaging Syst Technol, 22(1):53–66, 2012.
9. Wassermann D, Nikos M, Yogesh R et al. The white matter query language: a novel approach for describing human white matter anatomy. Brain Structure and Function, pages 1–17, 2016.
10. Caminiti R, Carducci F, Piervincenzi C et al. Diameter, Length, Speed, and Conduction Delay of Callosal Axons in Macaque Monkeys and Humans: Comparing Data from Histology and Magnetic Resonance Imaging Diffusion Tractography. Journal of Neuroscience 4 September 2013, 33 (36) 14501-14511.
11. Aboitiz F, Scheibel AB, Fisher RS and Zaidel E. Fiber composition of the human corpus callosum. Brain Research, 598(1–2):143 – 153, 1992.
12. Barazany D, Basser P, Assaf Y. In vivo measurement of axon diameter distribution in the corpus callosum of rat brain. Brain. 2009 May; 132(5): 1210–1220.
Figures