5242
Isotropic Diffusometry MRI of the human brain1NIBIB, National Institutes of Health, Bethesda, MD, United States, 2NINDS, National Institutes of Health, Bethesda, MD, United States, 3NICHD, National Institutes of Health, Bethesda, MD, United States
Synopsis
From diffusion MRI data acquired with isotropic diffusion encoding over a wide range of b-values, we estimate intravoxel distributions of mean diffusivities using a regularized Inverse Laplace Transform analysis. In vivo spectra of intra-voxel mean diffusivities measured in healthy subjects show consistent single-peak distributions in most brain regions, with subtle differences between white matter, cortical gray matter, subcortical gray matter, corpus callosum, and cerebrospinal fluid. This non-invasive, model-free, whole-brain approach to quantifying spectra of intrinsic tissue water mobilities could improve the clinical diagnosis and characterization of stroke, cancer, and other diseases.
Introduction
The mean apparent diffusion coefficient (mADC) obtained with diffusion tensor imaging (DTI)1 is an eloquent and robust clinical biomarker for diagnosing and characterizing ischemic stroke2, cancer3, and numerous other neurological disorders and diseases. In the human brain, the mADC measurement removes signal modulations from bulk diffusion anisotropy and provides an average measure of water mobility even in anisotropic white matter. Nevertheless, the value of mADC depends on experimental parameters such as diffusion sensitization (b-value) and diffusion time and is affected by restrictions at a microscopic scale (i.e., microscopic anisotropy), resulting in a biologically non-specific assessment of microstructure.
Recent studies4,5 suggest the possibility of quantifying average mADC values in microscopic water pools without biases due to microscopic anisotropy6. Isotropic diffusion encoding (IDE) with diffusion gradient waveforms specifically sensitized to multiple diffusion-diffusion correlations7-10 provides mADC-weighting for each microscopic water pool within the voxel.
In this study, we design an experiment for measuring clinical DWIs with IDE over a wide range of diffusion sensitizations (b-values). From these measurements, we estimate the probability distribution of intrinsic water mobilities in healthy human brain tissue. We compare and characterize these distributions of rotation-invariant mean diffusivity values using region-of-interest analysis (ROIs).
Methods
Three healthy volunteers were scanned using a spin echo EPI sequence with isotropic diffusion encoding (Fig. 1) on a clinical 3T scanner equipped with maximum gradient strength of 80 mT/m/axis. The pulse sequence in Fig. 1 is based on the original design proposed by Wong et al.8, and was modified to accommodate the presence of a 180° RF refocusing pulse and crusher gradients. The following imaging parameters were used: TE/TR=105/6000ms, 2.5x2.5x5mm resolution, 88x88 imaging matrix, 220x220cm field-of-view (FOV). DWIs were acquired at 60 b-values from 0 to 6000 s/mm2, with multiple averages for images with higher b-values. Diffusion datasets were processed with the TORTOISE software package11 to register all DWI volumes and correct EPI distortions due to eddy currents and field inhomogeneities.
From the IDE signal decays as a function of b-value we computed in each voxel a 1-D spectrum (i.e., probability distribution) of intravoxel intrinsic mean diffusivities using an Inverse Laplace Transform fit with positivity constraints and L2-norm regularization11. To improve the statistical power of our analysis, we generated regions-of-interest (ROIs) containing cerebrospinal fluid (CSF), white matter (WM), and gray matter (GM), subcortical gray matter (scGM) and quantified the average diffusivity spectra within each ROI.
Results
Characteristic values of signal-to-noise-ratio (SNR) in the non-diffusion attenuated (b=0s/mm2) images were 150 in white matter (WM), 250 in cortical gray matter (cGM), 110 in the corpus callosum (CC), 105 in subcortical gray matter (scGM), and 300 in the cerebro-spinal fluid (CSF). Numerical simulations using the abovementioned experimental design (number of DWIs and b-values) and SNR levels suggest that it is possible to reliably detect unimodal and bimodal intravoxel mean diffusivity distributions using our Inverse Laplace Transform analysis.
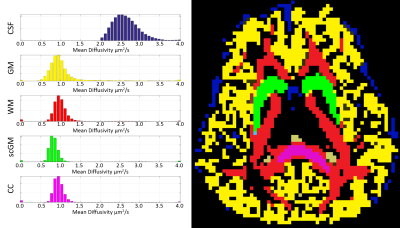
Preliminary results of this study reveal a remarkable consistency between average water mobilities in healthy human brain tissue. The diffusivity spectra in healthy brain tissues consistently show single-peak distributions with slight differences in peak locations and shapes. Distributions with multiple peaks were measured only in brain regions with significant tissue partial volume effects. Mean diffusivity spectra were generally broader in GM and narrower in WM, especially in the CC. Voxels containing CSF showed a distinctive, dominant peak with significantly faster mean diffusivity, as expected. The largest fractions of low diffusivity components <0.85 μm2/ms, were observed in scGM regions, in particular, the putamen, the globus pallidum, and caudate nucleus, and to a lesser extent the thalamus (Fig. 2).
Average normalized mean diffusivity spectra computed in regions of interest (ROIs) showed very consistent single-peak distributions of mean diffusivity values in GM, WM, scGM, and CC, with slight differences in the locations of the peak and shapes of the distribution (Fig. 3). Voxels at tissue interfaces were excluded from the ROIs to minimize contributions from partial volume effects.
Discussion
The unimodal distributions in brain parenchyma support assumptions of similar techniques, such as DIVIDE5 but also highlight the need for characterizing pathophysiological tissue changes by explicitly measuring distributions of intrinsic tissue water mobilities with model-free approaches.
The remarkable consistency of intrinsic water mobilities in healthy brain tissues may reflect a stability of water microdynamics associated with the homeostatic/energetic balance required for normal cellular metabolism. Future clinical studies will use isotropic diffusometry to explore how the striking changes in conventional mADC values in brain tissues with disrupted metabolism, e.g., changes in ischemic stroke or cancer therapy, are caused by diffusivity changes of (biologically) specific microscopic water pools.
Acknowledgements
This work was supported by the Intramural Research Program (IRP) of the National Institutes of Biomedical Imaging and Bioengineering (NIBIB) and the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) within the National Institutes of Health (NIH).References
1 Basser, P. J., Mattiello, J. & LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophys J 66, 259-267 (1994).
2 Moseley, M. E. et al. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magn Reson Med 14, 330-346 (1990).
3 Hamstra, D. A., Rehemtulla, A. & Ross, B. D. Diffusion Magnetic Resonance Imaging: A Biomarker for Treatment Response in Oncology. Journal of Clinical Oncology 25, 4104-4109, doi:10.1200/jco.2007.11.9610 (2007).
4 Topgaard, D. Multidimensional diffusion MRI. J Magn Reson 275, 98-113, doi:http://dx.doi.org/10.1016/j.jmr.2016.12.007 (2017).
5 Szczepankiewicz, F. et al. The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). Neuroimage 142, 522-532, doi:http://dx.doi.org/10.1016/j.neuroimage.2016.07.038 (2016).
6 Komlosh, M. E. et al. Detection of microscopic anisotropy in gray matter and in a novel tissue phantom using double Pulsed Gradient Spin Echo MR. J Magn Reson 189, 38-45, doi:10.1016/j.jmr.2007.07.003 (2007).
7 Mori, S., Crain, B. J., Chacko, V. P. & van Zijl, P. C. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 45, 265-269 (1999).
8 Wong, E. C., Cox, R. W. & Song, A. W. Optimized isotropic diffusion weighting. Magn Reson Med 34, 139-143 (1995).
9 Eriksson, S., Lasic, S. & Topgaard, D. Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. J Magn Reson 226, 13-18, doi:http://dx.doi.org/10.1016/j.jmr.2012.10.015 (2013).
10 Sjölund, J. et al. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 261, 157-168, doi:http://dx.doi.org/10.1016/j.jmr.2015.10.012 (2015).
11 Pierpaoli, C. et al. TORTOISE: an integrated software package for processing of diffusion MRI data. Book TORTOISE: an integrated software package for processing of diffusion MRI data (Editor ed.^ eds.) 18, 1597 (2010).
Figures
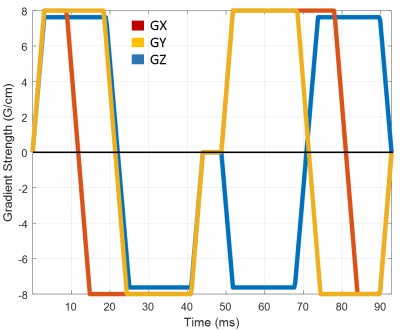
Figure 1: Diffusion gradient waveform for isotropic diffusion encoding with a wide range of b-values.Trapezoidal diffusion gradient pules are played out on all three physical axes GX, GY, GZ simultaneously to achieve an efficient isotropic diffusion encoding in a relatively short duration.