5239

Diffusion Weighting with Linear and Planar Encoding Solves Degeneracy in Parameter Estimation

Bibek Dhital¹, Marco Reisert¹, Elias Kellner¹, and Valerij G. Kiselev¹

¹Clinic for Radiology, Medical Physics, Faculty of Medicine, Medical Center - University of Freiburg, Germany, Freiburg, Germany

Synopsis

While estimating parameters of tissue microstructure models has never been simple, the recently discovered bi-modality (degeneration) of objective function in parameter space render it highly challenging. This study proposes a response to this challenge based on combining the commonly used linear encoding (the b-matrix with the diagonal 0,0,b) with the planar encoding (b,b,0). The signal was simulated in the whole parameter space of the standard model of brain white matter. Exhaustive search in this space demonstrates the absence of bi-modality when results for both encoding schemes are treated together.

Introduction

For diffusion-weighted microstructure imaging (DMI), water diffusivity in intra-axonal and extra-axonal compartments of the brain white matter is extremely difficult to estimate from commonly acquired multi-shell, multi-directiondata using the Stejskal-Tanner method [1]. Different parameter sets explain themeasured data equally well [2, 3]

In the presently common method, hereafter referred as linear encoding, the signal is sensitized to one direction during each measurement. Varying gradient direction during diffusion weighting can sensitize the signal to motion in two or three spatial direction (double or triple direction encoding) -- special cases of multi-direction encoding are isotropic encoding and the planar encoding for three and two orthogonal directions, respectively. Single direction, isotropic, and planar encoding are all equivalent for low diffusion weighting [4], but reveal complimentary information for stronger diffusion weighting [5].

This study was conducted to find out if the degeneracy in parameter estimation, which is inherent to multiple single-direction encoding [2, 3], can be resolved using complimentary information obtained from planar encoding.

Method

We use the standard model of white matter that considers DWI signal to arise from Watson-distributed blocks, each comprising axons and extra-axonal space without exchange. Diffusion in axons is one-dimensional and the diffusion in extra-axonal space is described by a tensor.

We simulated the signal for both linear and planar encoding varying the five parameters: intra-axonal diffusivity $$$D_I$$$, extra-axonal parallel diffusivity $$$D_{E\parallel}$$$, extra-axonal perpendicular diffusivity $$$D_{E\perp}$$$, intra-axonal volume fraction $$$v_I$$$ and the fiber dispersion concentration parameter $$$\kappa$$$ that defines the width of the assumed Watson distribution of the fiber orientation. $$$D_I$$$, $$$D_{E \parallel}$$$ and $$$D_{E \perp}$$$ were simulated for 20 points grid in the interval $$$[0.6,\,2.5]$$$, $$$[0.6,\,2.5]$$$ and $$$[0.1,\,2.0]\,\rm\mu m^2/ms$$$. The volume fraction, $$$v_I$$$, was linearly spaced in 16 points between [0.25, 0.75] and $$$\kappa$$$ was quadratically spaced with 11 points between $$$[0,\,100]$$$. Simulated signal was generated for each parameter set for both linear and planar encoding using 30 directions based on the concept of electrostatic repulsion and b-values of $$$1,\,2$$$ and $$$3\,\rm ms/\mu m^2$$$.

Out of 968000 parameter sets, we selected valid parameter sets that resulted in physically meaningful overall ADC values: $$$0.6< D_\parallel <2.5$$$ and $$$0.2<D_\perp <1$$$. For each of these valid parameter sets, we proceeded to find acceptable parameter sets where the reduced $$$\chi_R^2\,<\, 1.13$$$, at SNR of 100 for both the linear and the planar encoding. The intersection of these sets was selected as acceptable for both measurements.

Results

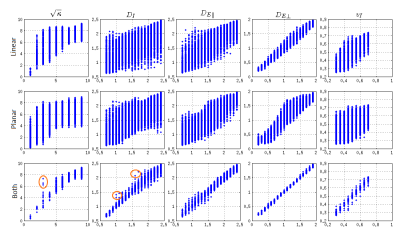
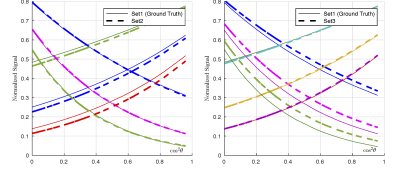
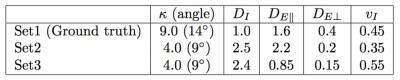
Both for linear encoding and for planar encoding, we find many completely different parameter sets that explain data rather well, in agreement with the previous results for the linear encoding [2,3]. We selected the mean of the acceptable parameters as an indicator of the degeneracy in parameter space; the broader the parameter distribution the more its mean deviated from the ground truth. In Figure 1, we show the mean of all acceptable parameters plotted against the ground truth for (i) for linear encoding (top row), (ii) for planar encoding (mid row). It can be seen that in many cases linear or planar encoding both have issues regarding degeneracy where completely different parameter sets result in similar signal. In Figure 1 (bottom row) we show the mean of parameter sets that were acceptable for both linear and planar encoding. These parameter sets are in the vicinity of the ground truth. The deviation of the mean values from the ground truth was mainly due to the resolution of our simulation grid. Some residual dispersion in the parameters is explained by the shallow optimization landscape (shown in red in Figure 1), not the discussed discrete degeneracy of parameter estimate. To further clarify this position, in Figure 2 we show simulated signal for three essentially different parameters sets, 1, 2, and 3, with the parameters specified in Table 1. $$$\rm\,Set\,1$$$ is taken as ground truth for illustration purposes. The right panel in Figure 2 shows that $$$\rm\,Set\,2$$$ is acceptable by linear encoding, but ruled out by planar encoding. The left panel shows the opposite for $$$\rm\,Set\,3$$$, which is ruled out by linear encoding while acceptable by planar encoding. Therefore, $$$\rm\,Set\,2$$$ could have been a false result if only linear encoding was used and $$$\rm\,Set\,3$$$ if only planar encoding was used. The usage of both linear and planar encoding helps discriminate the correct solution ( $$$\rm\,Set\,1$$$) from the false ones.

Discussion

Signal simulations accompanied by the exhaustive search in parameter space suggests that microstructural imaging with a combination of linear and planar encoding resolves the degeneracy in parameter estimation. This generalizes the previous evidence obtained for three particular data sets using the logic of double PFG [6]. Our further work is focused on approaching the problem through analytical framework and running measurements in-vivo.

Acknowledgements

References

[1] Edward O Stejskal and John E Tanner. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. The Journal of Chemical Physics, 42(1):288–292, 1965.

[2] Ileana O Jelescu, Jelle Veraart, Els Fieremans, and Dmitry S Novikov. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue.NMR in Biomedicine, 29(1):33–47, 2016.

[3] Dmitry S. Novikov, Jelle Veraart, Ileana O Jelescu, and Els Fieremans. Mapping orientational and microstructural metrics of neuronal integrity within vivo diffusion MRI. https://arxiv.org/abs/1609.09144.

[4] Sune Nørhøj Jespersen. Equivalence of double and single wave vector diffusion contrast at low diffusion weighting. NMR in Biomedicine, 25(6):813–818, 2012.

[5] Carl-Fredrik Westin, Hans Knutsson, Ofer Pasternak, Filip Szczepankiewicz, Evren Özarslan, Danielle van Westen, Cecilia Mattisson, Mats Bogren, Lauren J O’donnell, Marek Kubicki, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage, 135:345–362,2016.

[6] Santiago Coelho, Leandro Beltrachini, Jose M. Pozo, and Alejandro F. Frangi. Double diffusion encoding vs single diffusion encoding in parameter estimation of biophysical models in diffusion-weighted MRI. In proc. Annual Meeting of ISMRM, 2017, page 3383.

Figures

FIGURE 1: Mean of acceptable parameters plotted against their corresponding ground truth for linear encoding (top row), planar encoding (mid row) and the parameter intersection of both linear and planar encoding (bottom row). It is seen that the intersection of the two resolves the degeneracy in parameter selection so that the resulting mean value is close to the ground truth.

FIGURE 2: Signal generated for three parameter sets specified in Table 1 for three b-shells (from top to bottom). The signal as a function of $$$ \cos^2\theta $$$ increases for linear encoding and decreases for planar encoding. Although the underlying parameters are very different, signal from Set 2 is close to the ground truth for linear encoding (left) and signal from Set 3 is very similar to the ground truth for planar encoding (right). Combination of both encodings unambiguously selects the ground truth (Set 1).

TABLE 1: Microstructural parameters used for illustration purpose in Figure 2. All diffusivities are measured in $$$\rm \mu m^2/ms$$$, $$$\kappa$$$, $$$v_I$$$ are dimensionless and `angle' is the width of Watson distribution, $$$\arcsin(1/(2\kappa))$$$.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

5239