5237
Voxel size matters: big voxels are required to generate realistic extra-axonal dMRI signals from Monte Carlo simulations1Signal Processing Lab 5 (LTS5), EPFL, Lausanne, Switzerland, 2Danish Research Centre for Magnetic Resonance, Center for Functional and Diagnostic Imaging and Research, Copenhagen University Hospital Hvidovre, Hvidovre, Denmark, 3Centre d'Imagerie Biomédicale, EPFL, Lausanne, Switzerland, 4Department of Applied Mathematics and Computer Science, Technical University of Denmark, Kongens Lyngby, Denmark, 5Department of Radiology, University Hospital Center (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 6Computer Science department, University of Verona, Verona, Italy
Synopsis
Monte Carlo simulations provide diffusion MRI signals that can be used to evaluate microstructure models, but that can also be incorporated into microstructure reconstruction methods. It is therefore important for the generated signals to be as realistic as possible. This work shows preliminary evidence that, in the case of white matter models, the symmetry of the perpendicular extra-axonal signal generated with Monte Carlo simulations depends on the voxel size. Simulations corresponding to millimeter-sized voxels should therefore be computed using substrates of equivalent size, or by averaging signals generated from multiple small voxels.
Introduction
Diffusion MRI (dMRI) can in principle be used to recover White Matter (WM) microstructure properties, like the mean axon diameter,1 density1, dispersion2 and diameter distributions.3 by fitting biophysical models to the dMRI signal.1,2,3 Such models assume the WM tissue to consist of three compartments: an impermeable and restricted compartment representing the intra-cellular space i.e. axons, a hindered compartment representing the extra-axonal (EA) space between axons and an isotropic compartment accounting for free diffusion (e.g. partial volume with cortico spinal fluid). Real acquisitions involve voxel resolutions of the order of 500x500um2 for animal imaging and 2.0x2.0mm2 for humans. Given this voxel size, the hindered signal perpendicular to the axons should be isotropic and is therefore usually modeled as a symmetric tensor.4 As simulating dMRI signals for such voxel sizes is demanding in terms of memory and computation time, Monte Carlo simulations are usually performed in voxels of much smaller size.1,5 In this study, we explored the influence of voxel size on the EA signal generated from Monte Carlo simulations.Methods
We created voxels with different sizes ranging from 40.5x40.5μm2 to 406x406μm2, all with the same intra-cellular volume fraction (ICVF=0.60) and same diameter distributions: 100 radii were initially sampled from a gamma distribution 𝛤(3.27,4.91E-7)1 and then used to generate the different substrates. The final voxel size was adapted to achieve a ICVF=0.60 and periodical boundaries were accounted as in.5 An in-house Monte Carlo simulator was used to generate the EA signal with the following settings: 1x106 spins in the EA space, diffusivity of 1.7x10-9m2.s-1, TE=75ms and 5000 steps. The following diffusion protocol was used: G=300mT/m, delta=10ms and Delta from 15 to 100ms, acquired in 180 directions evenly distributed over the xy-plane.Results and discussion
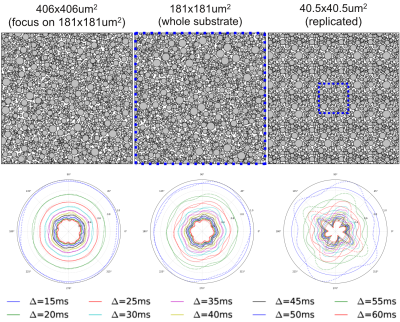
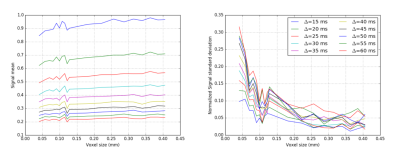
Figure 1 shows samples of cylinder positions for three different substrates, as well as the corresponding EA signals. Figure 2 shows the mean and standard deviation of the EA signal as a function of substrate size. Overall, our experiments show that EA signals from real acquisitions (voxel sizes of the order of millimeters) cannot be approximated by using Monte Carlo simulations in small voxels. Indeed, small voxels present EA signals that are not symmetric, and with reduced mean amplitude compared to signals from bigger voxels. Voxel sizes of the order of 400x400μm2, which is the typical voxel size for animal imaging, are therefore required to be able to generate realistic EA signals that are in accordance with biophysical models for hindered compartments.
The symmetry of the EA signal can also be recovered by averaging many small substrates. We averaged the signals of 100 substrates of size 40.5x40.5μm2 (each with different cylinder positions) and obtained an EA signal with standard deviation and amplitude equivalent to the signal obtained for a voxel of 406x406μm2. Our observations regarding single voxels might therefore be linked to the limited number of cylinders in small voxels, which limits the diversity of local environments explored by the spins when the voxel size is small.
Conclusion
The EA signal is influenced by the voxel size. To approximate dMRI signals for millimeter-sized voxels, Monte-Carlo simulations should be performed using equivalent voxel sizes. If simulations with a high number of cylinders is not feasible (e.g. due to memory limitations), the signal should be averaged from several small substrates in order to obtain reliable measures. Future work will focus on evaluating the effect of voxel size on the mean squared displacement, and the influence of other simulation parameters on the dMRI signal, as gradient strength and duration, the water diffusivity, the size of cylinders as well as their packing density.Acknowledgements
This project was funded by the Swiss National Foundation, grant 31003A_157063References
1. D. C. Alexander, P. L. Hubbard, M. G. Hall, E. A. Moore, M. Ptito, G. J. M. Parker, et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage. 2010;52:1374.
2. H. Zhang, T. Schneider, C.A. Wheeler-Kingshott, D.C. Alexander. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage. 2012;61:1000-1016
3. Y. Assaf, T. Blumenfeld-Katzir, Y. Yovel, and P. J. Basser. AxCaliber: a method for measuring axondiameter distribution from diffusion MRI. Magn. Reson. Med. 2008;59:1347
4. E. Panagiotaki, T. Schneider, B. Siow, M. G. Hall, M. F. Lythgoe, and D. C. Alexander. Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison. Neuroimage. 2012;59:2241.
5.
M. G. Hall and D. C. Alexander. Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE Trans. Med. Imaging 2009;28:1354–1364
Figures